[POJ]POJ 3678 Katu Puzzle

前言

传送门 :

题意 : 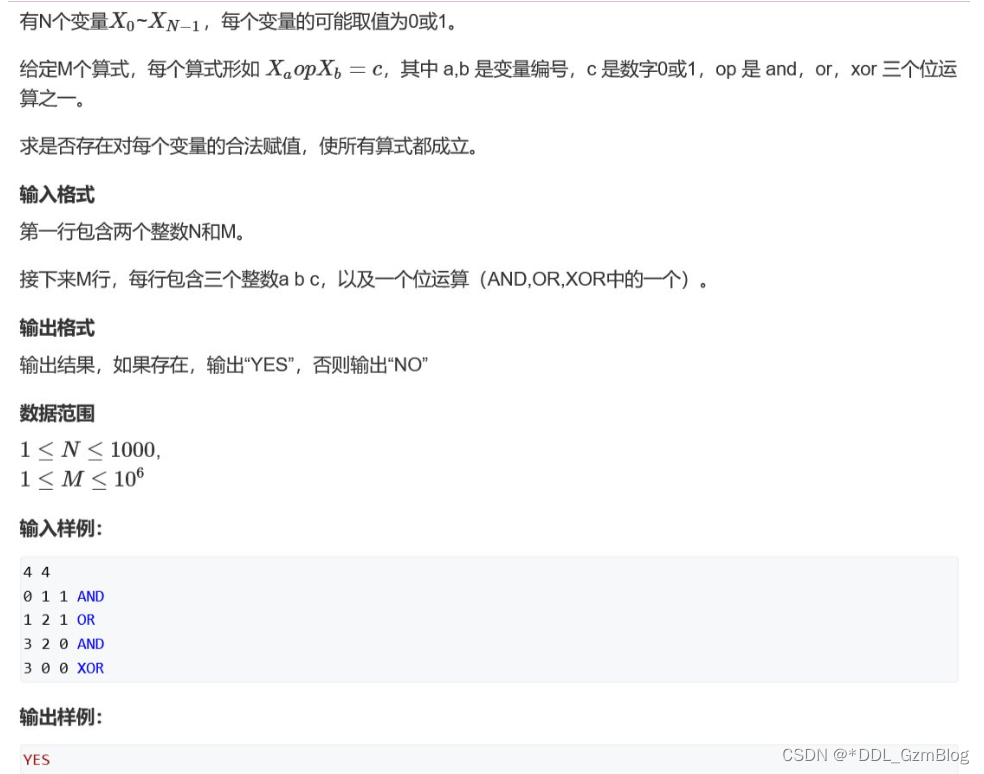思路 : 每个元素只有两种可能的取值 0 , 1 0,1 0,1,并且还是求是否存在合法值使得满足所有条件

因此这是典型的 2 − S A T 2-SAT 2−SAT问题

我们对于给定的 n n n个点,取 [ 1... n ] [1...n] [1...n]表示 x x x取 0 0 0,取 [ n + 1.... n + n ] [n+1....n+n] [n+1....n+n]表示 x x x取 1 1 1

下面考虑建边 :

(摘自繁凡)

建完边之后,我们只需要跑一边强连通分量 S C C SCC SCC,对于矛盾的关系 s c c [ x ] = = s c c [ x + n ] scc[x]==scc[x+n] scc[x]==scc[x+n]存在那么必然无解

code :

// Problem: Katu Puzzle
// Contest: POJ - POJ Founder Monthly Contest – 2008.07.27
// URL: http://poj.org/problem?id=3678
// Memory Limit: 65 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

const int N = 4e6+10,INF = 0x3f3f3f3f;
const double eps = 1e-5;


int h[N],e[N],ne[N],idx;


int dfn[N],low[N],timestamp;
int id[N],scc_cnt,in_stk[N],top,stk[N];

void add(int a,int b){
	ne[++idx]  = h[a] ,e[idx] = b,h[a] = idx;
}
void tarjan(int u)
{
    dfn[u] = low[u] = ++timestamp;
    
    stk[++top] = u ;
    in_stk[u] = true;
    
    for(int i = h[u];i;i=ne[i])
    {
        int j = e[i];
        if(!dfn[j])
        {
            tarjan(j);
            low[u] =min(low[u],low[j]);
        }else if(in_stk[j])
            low[u] =min(low[u],dfn[u]);
    }
    if(dfn[u] == low[u])
    {
        int y;
        ++scc_cnt;
        
        do{
            y = stk[top--];
            in_stk[y] =false;
            id[y] = scc_cnt;
        }while(y!=u);
    }
}

int n,m;
char s[N];

void solve(){
	cin>>n>>m;
	while(m -- ){
		int a,b,c;cin>>a>>b>>c;
		a++;
		b++;
		
		std::cin>>s;
		///cout