[算法基础课] AcWing 787. 归并排序

前言

时间复杂度 : O ( n l o g n ) O(nlogn) O(nlogn) Tag :归并排序逆序对 传送门 :

思路

回顾归并思路 :

1. 将区间一分为二
2. 递归排序区间
3. 合并区间

对于逆序对,我们发现在递归过程中,我们只有两种情况需要考虑

1. 在同一个区间的逆序对
2. 不在同一个区间的逆序对

因为归并排序每次都会将大区间划分为小区间,即一个分治的过程

所以最后(1) 在同一个区间的逆序对其实是包含在(2)内的

因此我们考虑(2)是如何计算的

我们设已经排好序的左右区间是L,R, 那么考虑如图情况

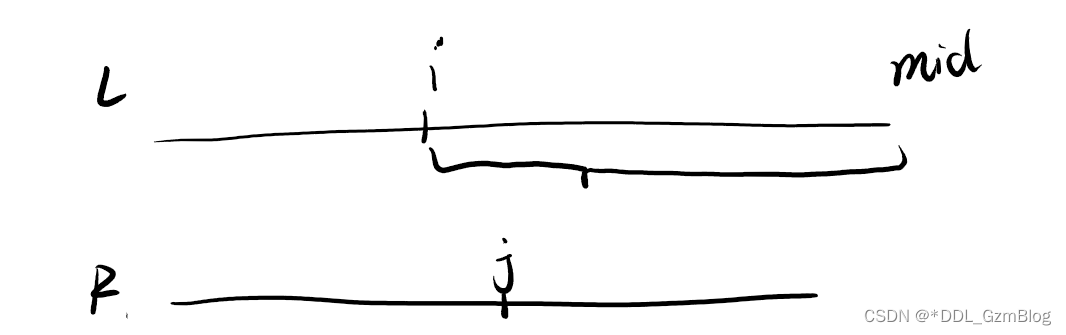如果L[i] > R[j]那么i前面的数必然不能比R[j]大,因为已经排好序,而其后面的数一定大于R[j]

因此对于当前的j会贡献mid-i+1个逆序对

因此我们根据这个公式分治即可

代码

LL merge_sort(int q[], int l, int r) { if (l >= r) return 0; int mid = l + r >> 1; LL res = merge_sort(q, l, mid) + merge_sort(q, mid + 1, r); int k = 0, i = l, j = mid + 1; while (i <= mid && j <= r) if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ]; else { res += mid - i + 1; //计算答案 tmp[k ++ ] = q[j ++ ]; } while (i <= mid) tmp[k ++ ] = q[i ++ ]; while (j <= r) tmp[k ++ ] = q[j ++ ]; for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j]; return res; }