洛谷P2486 [SDOI2011]染色（树链剖分初入门）

首先,根据本人以往解决经验这类疑似树上区间操作,都可能是树链剖分,我们先考虑数组的实现情况 给你一个数组 a i ai ai,有2个操作 操作 1 : [ l , r , c o l o r ] : [ l , r ] 变成 c o l o r 色 操作1:[l,r,color]:[l,r]变成color色 操作1:[l,r,color]:[l,r]变成color色 操作 2 : 查询 [ l , r ] 颜色段的数目 操作2:查询[l,r]颜色段的数目 操作2:查询[l,r]颜色段的数目 这是线段树染色的一个东西,解决方法如下: 线段树维护3个值 区间颜色数量 n u m , 左端点颜色 c l , 右端点颜色 c r 区间颜色数量num,左端点颜色cl,右端点颜色cr 区间颜色数量num,左端点颜色cl,右端点颜色cr 考虑区间之间的合并: 如果左区间 L L L的 c r cr cr与右区间 R R R的 c l cl cl一样,说明有一段染色横跨了两个区间.那么总的染色数目会减少1. n u m [ f a ] = n u m [ L ] + n u m [ R ] − 1 num[fa]=num[L]+num[R]-1 num[fa]=num[L]+num[R]−1 否则,两个区间之间没有交叉,颜色数目都是独立的. n u m [ f a ] = n u m [ L ] + n u m [ R ] num[fa]=num[L]+num[R] num[fa]=num[L]+num[R] 解决完核心的区间合并问题,我们就可以尝试书写线段树部分并套用树链剖分即可. 很快我们发现仍然有问题,因为线段树部分只能在重链部分是有效的,我们需要人为去合并重链之间的信息. 当让 d e p t h [ x ] depth[x] depth[x]较大的点往上跳的时候,记录前一次跳的时候较浅的点的颜色(就是线段树查询里边的左端点的颜色,因为深度小的结点在线段树映射的id也小),如果查询到的链条的右端点与上一次的左端点颜色相同,那么它们本来是同一段颜色,应当减一. 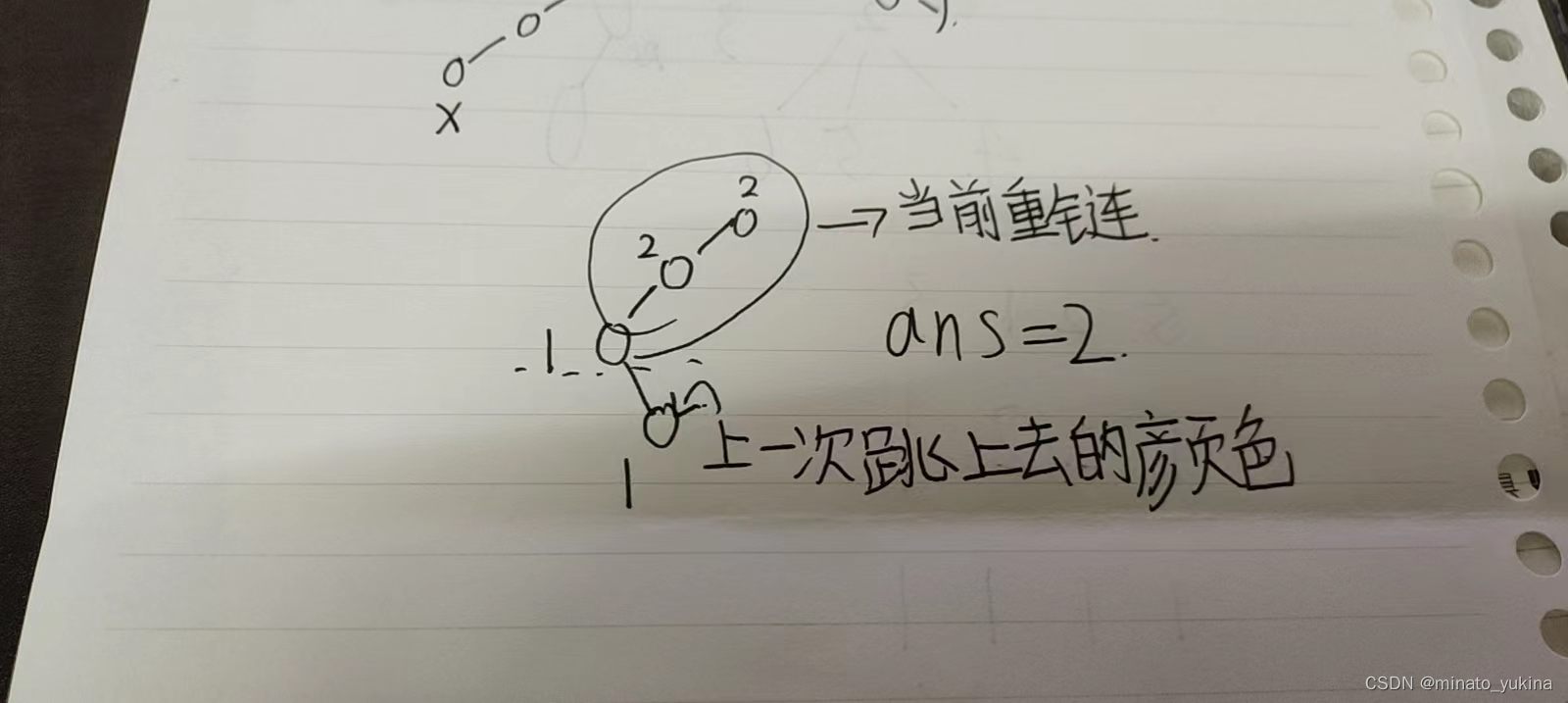基于这个想法:我们用 c l cl cl记录上一次 x x x跳完后左端点区间的颜色,也就是 t o p [ x ] top[x] top[x]的颜色,用 c r cr cr记录 c l cl cl上一次更替的值. 首先, c l cl cl是为了帮助我们解决上边的问题的,也就是 x x x往上跳到新的重链的时候, 之前的 t o p [ x ] 之前的top[x] 之前的top[x]与新链最下边的颜色是否相同,如果相同那么则要减少1,因为他们属于同一个颜色块. 有代码 i f ( c l = = t . c r ) a n s − − if(cl==t.cr) ans-- if(cl==t.cr)ans−−, t . c r t.cr t.cr是本次跳到新链后最下边的那个点. 然而,因为这个 x x x跳到 L c a ( x , y ) Lca(x,y) Lca(x,y)的过程是两个点反复横跳的过程,所以我们还需要一个 c r cr cr来记录另外一边(也就是y那边)对应的那个 c l cl cl. 当我们执行了 i f ( d e p t h [ t o p [ x ] ] < d e p t h [ t o p [ y ] ] ) s w a p ( x , y ) if(depth[top[x]]u>>v; G[u].pb(v);G[v].pb(u); } dfs1(1,0); dfs2(1,1); build(1,1,n); while(m--){ char op;cin>>op; if(op=='C'){ int a,b,c;cin>>a>>b>>c; tr_update(a,b,c); } else{ int a,b;cin>>a>>b; cout