矩阵快速幂的意思就是进行快速幂运算的是矩阵。
快速幂的知识我在这就不讲了,不知道的可以看Here
矩阵快速幂的本质是将递推公式转换为幂次运算,幂次运算又可以通过快速幂算法来快速实现,从而降低了时间复杂度。
矩阵快速幂中要进行幂次操作的是矩阵,矩阵的幂次操作就是矩阵进行多次相乘,那我们就先来了解一下矩阵乘法: A * B = C,其中A、B、C均为矩阵,且A、B、C满足规格要求:A:n×k、B:k×m、C:n×m。 其中C[i][j]为A的第i行与B的第j列对应乘积的和。(线性代数基础)
矩阵乘法代码如下:
struct Matrix { // 我比较喜欢用结构体存一个二维数组表示矩阵,因为传参的时候可以传结构体,而不是一个二维数组
int m[N][N];
};
Matrix Matrix_mul(Matrix a, Matrix b) {
Matrix c;
for(int i = 1;i >=1;
}
return res;
}
为什么矩阵快速幂中的res要初始化为单位矩阵?这与快速幂代码中要将res初始化为1的道理类似,矩阵乘法中任何矩阵乘单位矩阵都是矩阵本身,作用与数值乘法中的1一致,这里的单位矩阵就是起到这样的作用。
以上就是矩阵快速幂的基础知识了,下面我们针对本题来说一下如何使用矩阵快速幂解决问题。
我们可以将斐波那契数列的递推公式f(n) = f(n-1) + f(n-2),转换为矩阵形式(好神奇): 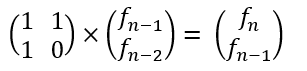 简写成
简写成T * A(n-1) = A(n),T矩阵就是那个2×2的常数矩阵,我们发现数列A就是一个等比数列,公比为常数矩阵T。那我们知道了A(1)之后通过矩阵快速幂不就可以实现计算常数矩阵T的若干次幂了嘛。 举几个例子可以发现,我们要求f(n),对常数矩阵T进行n次幂的操作后得到的矩阵右上角位置的数即为f(n)的值。 快速幂的时间复杂度是O(logn),因此我们将时间复杂度从O(n)降至O(logn)。
一些其他的递推式变形(感觉蓝桥杯会个Fib的就不错了): 
矩阵快速幂模板 对应代码
矩阵快速幂应用 对应代码



