控制算法学习 二、PID控制算法

前言

PID应该是应用最广泛的控制算法（没有之一）。无人机中的飞控就是基于PID的。

PID算法

PID——Proportional, Integral, Derivate，就是比例-积分-微分控制。

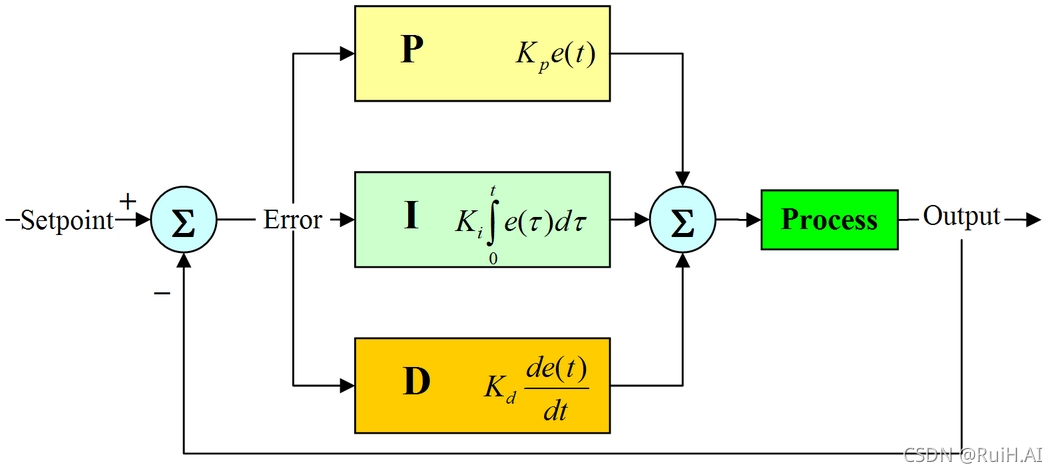PID的控制公式如下： u ( t ) = K p e ( t ) + K i ∫ 0 t e ( σ ) d σ + K d d e ( t ) d t \begin{aligned} & u(t)=K_pe(t)+K_i \int_0^t e(\sigma)d\sigma +K_d \frac{de(t)} {dt} \\ \end{aligned} ​u(t)=Kp​e(t)+Ki​∫0t​e(σ)dσ+Kd​dtde(t)​​ K p K_p Kp​——比例增益 K i K_i Ki​——积分增益 K d K_d Kd​——微分增益

比例环节P

由控制量和期望量的误差与比例增益 K p K_p Kp​加权产生，用于迅速减小控制量与期望量之间的差距。

K p K_p Kp​越大，过渡时间越快，稳态误差越小，但容易出现振荡不稳。

积分环节I

由误差的累计与积分增益 K i K_i Ki​加权产生，用于消除稳态误差。

K i K_i Ki​越大，消除稳态误差速度越快，但容易出现振荡不稳，超调量增加，达到稳定的时间延后。

微分环节D

由误差的变化速度与微分增益 K d K_d Kd​加权产生，用于阻尼误差的产生，减少超调量。

K d K_d Kd​越大，超调量降低，稳定性上升，达到稳定的时间提前，但容易受到输入噪声的影响。

离散PID

标准PID公式建立在连续状态空间中，而实际场景应用是，控制算法需要进行离散化，有两种离散化方法。

位置式PID

u ( T ) = K p e ( T ) + K i ∑ n = 0 T e ( n ) + K d [ e ( T ) − e ( T − 1 ) ] \begin{aligned} & u(T)=K_pe(T)+K_i \sum_{n=0}^Te(n) +K_d [e(T)-e(T-1)] \\ \end{aligned} ​u(T)=Kp​e(T)+Ki​n=0∑T​e(n)+Kd​[e(T)−e(T−1)]​ 优点：非递推，控制量与当前状态对应。 缺点：误差需要从开始累加到当前，计算量大。

增量式PID

Δ u ( T ) = K p [ e ( T ) − e ( T − 1 ) ] + k i e ( T ) + K d [ e ( T ) − 2 e ( T − 1 ) + e ( T − 2 ) ] u ( T ) = u ( T − 1 ) + Δ u ( T ) \Delta u(T) = K_p[e(T)-e(T-1)] + k_ie(T)+K_d[e(T)-2e(T-1)+e(T-2)] \\ u(T)=u(T-1)+\Delta u(T) Δu(T)=Kp​[e(T)−e(T−1)]+ki​e(T)+Kd​[e(T)−2e(T−1)+e(T−2)]u(T)=u(T−1)+Δu(T) 优点：控制增量仅与近三次误差量相关，计算量小。 缺点：有稳态误差。