Python numpy使用记录5.生成球面斐波那契网格

前言

本篇学习使用numpy生成球面斐波那契网格。

斐波那契网格公式

对于一个球体，要在球体表面上均匀选取N个点，就可以使用斐波那契网格公式： z n = r ( 2 n − 1 N − 1 ) x n = r 1 − z n 2 ⋅ cos ⁡ ( 2 π n ϕ ) y n = r 1 − z n 2 ⋅ sin ⁡ ( 2 π n ϕ ) ϕ = 5 − 1 2 z_n = r(\frac{2n-1}{N} - 1) \\ \quad \\ x_n = r\sqrt{1-z_n^2}\cdot \cos(2\pi n\phi) \\ \quad \\ y_n = r\sqrt{1-z_n^2}\cdot \sin(2\pi n\phi) \\ \quad \\ \phi = \frac{\sqrt{5} - 1}{2} zn​=r(N2n−1​−1)xn​=r1−zn2​ ​⋅cos(2πnϕ)yn​=r1−zn2​ ​⋅sin(2πnϕ)ϕ=25 ​−1​ 其中， r r r表示球半径， ϕ \phi ϕ即黄金分割比例。

代码

通过numpy形成斐波那契网格点云，然后通过open3d来可视化点云图：

import open3d as o3d
import cv2
import numpy as np


if __name__ == '__main__':
    vis = o3d.visualization.Visualizer()
    N = 1000
    r = 1
    phi = (np.sqrt(5) - 1) / 2
    n = np.arange(0, N)
    z = ((2*n + 1) / N - 1)
    x = (np.sqrt(1 - z**2)) * np.cos(2 * np.pi * (n + 1) * phi)
    y = (np.sqrt(1 - z**2)) * np.sin(2 * np.pi * (n + 1) * phi)
    print(z.shape, x.shape, y.shape)
    pcd = r * np.stack([x, y, z], axis=-1)
    print(pcd.shape)
    point_cloud = o3d.geometry.PointCloud()
    point_cloud.points = o3d.utility.Vector3dVector(pcd)
    vis.add_geometry(point_cloud)
    o3d.visualization.draw_geometries([point_cloud])

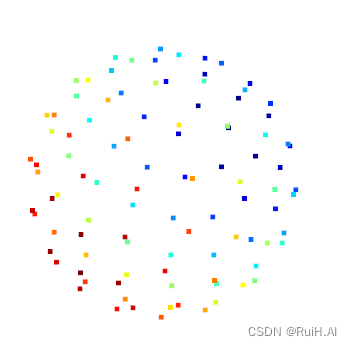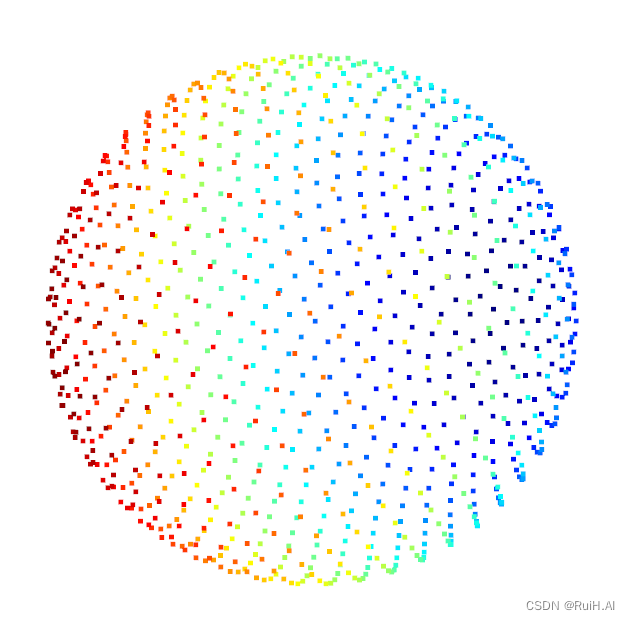
取100个点的效果： 取1000个点的效果：