个人Limitの线段树题单题解主目录:Limitの线段树题单 题解目录_HeartFireY的博客-CSDN博客
要求支持子树 01 01 01反转,子树求和。
树剖序列化一下,然后按照 0 − 1 0-1 0−1序列反转板子来就可以。
洛谷传送门:CF877E Danil and a Part-time Job - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
CF传送门:E. Danil and a Part-time Job (codeforces.com)
题目分析大水题
有一棵 n n n 个点的树,根结点为 1 1 1 号点,每个点的权值都是 1 1 1 或 0 0 0
共有 m m m 次操作,操作分为两种
-
g e t get get 询问一个点 x x x 的子树里有多少个 1 1 1
-
p o w pow pow 将一个点 x x x 的子树中所有节点取反
对于每个 g e t get get 给出答案
首先树剖将树序列化,然后建线段树维护 0 − 1 0-1 0−1序列反转(建树初始化标记为 − 1 -1 −1,然后下放容斥即可)。
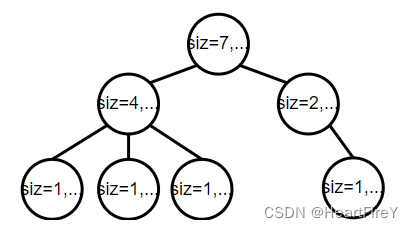
如上图,我们对一颗树求 d f n dfn dfn序及子树 s i z siz siz,不难发现同一子树内编号连续,那么可以将树映射到线段树上的连续区间, r t rt rt的子树就可以表示为 d f n [ r t ] + s i z [ r t ] − 1 dfn[rt] + siz[rt] - 1 dfn[rt]+siz[rt]−1。
属于非常经典的树上问题序列化且非常板。
Code#include #pragma gcc optimize("O2") #pragma g++ optimize("O2") #define int long long #define endl '\n' using namespace std; const int N = 2e5 + 10, MOD = 1e9 + 7; //快读板子 namespace ffastIO { inline int read(){ int f = 1, x = 0; char s = getchar(); while(s < '0'||s > '9'){ if(s == '-') f = -1; s = getchar(); } while(s >= '0' && s <= '9'){ x = x * 10 + s - '0'; s = getchar();} return x *= f; } } using ffastIO::read; std::vector<int> g[N]; int a[N], pfa[N], dep[N], siz[N], son[N], top[N], dfn[N], rnk[N], ind; int n, m; void dfs1(int u, int fa){ pfa[u] = fa, dep[u] = dep[fa] + 1, siz[u] = 1; for(auto &v : g[u]){ if(v == fa) continue; dfs1(v, u); siz[u] += siz[v]; if(siz[v] > siz[son[u]]) son[u] = v; } } void dfs2(int u, int tp){ dfn[u] = ++ind, rnk[ind] = u, top[u] = tp; if(!son[u]) return; dfs2(son[u], tp); for(auto & v: g[u]){ if(v == pfa[u] || v == son[u]) continue; dfs2(v, v); } } namespace SegTree{ #define ls rt << 1 #define rs rt << 1 | 1 #define lson ls, l, mid #define rson rs, mid + 1, r int tree[N << 2]; bool flip_tag[N << 2]; void push_up(int rt){ tree[rt] = tree[ls] + tree[rs]; } void build(int rt, int l, int r){ if(l == r) return (void)(tree[rt] = a[rnk[l]]); int mid = l + r >> 1; build(lson), build(rson); push_up(rt); } void push_down_flip(int rt, int m){ if(!flip_tag[rt]) return; flip_tag[ls] ^= 1, flip_tag[rs] ^= 1; tree[ls] = (m - (m >> 1)) - tree[ls]; tree[rs] = (m >> 1) - tree[rs]; flip_tag[rt] = 0; } void flip(int rt, int l, int r, int L, int R){ if(l >= L && r <= R){ flip_tag[rt] ^= 1; tree[rt] = (r - l + 1) - tree[rt]; return; } push_down_flip(rt, r - l + 1); int mid = l + r >> 1; if(mid >= L) flip(lson, L, R); if(mid < R) flip(rson, L, R); push_up(rt); } int query(int rt, int l, int r, int L, int R){ if(l >= L && r <= R) return tree[rt]; push_down_flip(rt, r - l + 1); int mid = l + r >> 1, ans = 0; if(mid >= L) ans += query(lson, L, R); if(mid < R) ans += query(rson, L, R); return ans; } #undef ls #undef rs #undef lson #undef rson } inline void solve(){ n = read(); for(int i = 2; i <= n; i++){ int v; cin >> v; g[v].emplace_back(i); } for(int i = 1; i <= n; i++) a[i] = read(); dfs1(1, 0), dfs2(1, 1); m = read(); SegTree::build(1, 1, n); for(int i = 1; i <= m; i++){ string op; cin >> op; int st = read(); if(op[0] == 'g') cout << SegTree::query(1, 1, n, dfn[st], dfn[st] + siz[st] - 1) << endl; else SegTree::flip(1, 1, n, dfn[st], dfn[st] + siz[st] - 1); } } signed main(){ solve(); return 0; }



