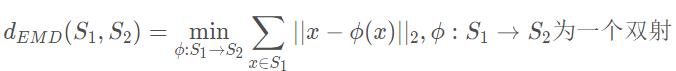点云质量评估_点云配准中常用的评价指标

目录

1.概述

2.豪斯多夫距离（Hausdorff Distance，HD）

3.倒角距离（Chamfer Distance，CD）

4.陆地移动距离（Earth Mover’s Distance，EMD）

1.概述

在点云配准问题中，我们通常会用相似性测度来评价两组点云之间的匹配程度，或作为迭代求解的代价方程（cost function），常见的相似性测度有均方误差（Root Mean Square Error（RMSE）、最大公共点集（Largest Common Pointset，LCP） 等。此外，还有豪斯多夫距离（Hausdorff Distance，HD）、倒角距离（Chamfer Distance，CD）和陆地移动距离（Earth Mover’s Distance，EMD）等指标也可被用于评价点云之间的匹配程度。

2.豪斯多夫距离（Hausdorff Distance，HD）

Hausdorff距离描述了度量空间中真子集之间的距离。假设有两个集合

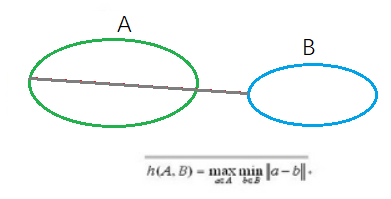
 则这两个集合之间的Hausdorff距离定义为：

•  其中，H(A,B) 被称为集合A和B之间的双向Hausdorff距离，是Hausdorff距离的最基本形式;
• ‖·‖是点集A和B点集间的距离范式(如:L2或Euclidean距离).
• 下面的式子中的h(A,B)和h(B,A)分别称为从A集合到B集合和从B集合到A集合的单向Hausdorff距离.
  • 即h(A,B)实际上首先对点集A中的每个点ai，到距离ai点最近的B集合中点bj之间的距离‖ai-bj‖，（比如A集合中有100个点，就有100个上述最小值）然后进行排序, 然后取该距离中的最大值（100个最小值中的最大值）作为h(A,B)的值. h(B,A)同理可得.
• 由上面的式子知,双向Hausdorff距离H(A,B)是单向距离h(A,B)和h(B,A)两者中的较大者,
• 它度量了两个点集间的最大不匹配程度.
• 

改进的Hausdorff距离

•  参考代码1（matlab版） 
•  参考代码2 matlab官方

•  参考：Hausdorff 距离

3.倒角距离（Chamfer Distance，CD）

给定两个点集S1 和S2, 它们之间的Chamfer Distance定义为：

4.陆地移动距离（Earth Mover’s Distance，EMD）

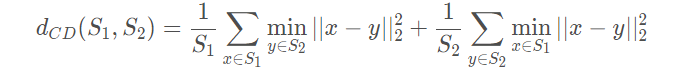
给定两个点集S1 和S2, 它们之间的Earth Mover’s Distance定义为：