深度学习笔记_基本概念_梯度下降及示例代码

目录

1. 什么是梯度下降法？

2. 举个例子

3. 完整代码示例

1. 什么是梯度下降法？

以函数求解最小值为例：

y= x^2:  改变自变量x的值，让梯度y’（自变量的导数dy/dx=2x）逐渐减小到0，从而使因变量y达到最小。

以求解模型参数为例：

y = ax+b:  我们想要通过采样值(x,y) 求解模型中参数a和b, 则需要构造一个损失函数loss：

loss =(ax+b – y)^2: 求使loss最小时的a和b. 即等价于函数求解最小值。

更详细的说：

例如：y = x^2

y’ = 2x = g(x);

设初始 x0 = -10, 则 y’_0 = -20

…

y’_n = y’_o - g(x) 其中 x = x0 – δx, 这样x一直变化，直到y’等于0，就找到了极小值。

学习率的引入： δx一次变化太多可能导致震动，或者找不到最优解，所以给它乘以一个系数 lr, 让x的变化量每次能小一点。所以 x =  x0 - δx * lr        

2. 举个例子

比如需要求模型 y = wx + b 中 的模型参数b和w, 我们有一系列的采样值 (x,y)，怎样用梯度下降法求b和w呢？

首先构造损失函数 loss = (wx+b -y)^2, 当损失函数取最小值时，我们在上述采样值上则找到最佳的w和b。

定义损失函数： 

梯度下降（更新待求解参数w）: 给定w或b的初值，更新这个初值w，直到收敛到一个稳定的值（稳定时，梯度为0,  模型参数不再变化，损失函数取到最小值）：

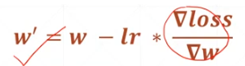
迭代：当然采样（x,y）是多组参数，所以更新梯度时，可以使用的多组采样点的平均值。每次使用所有的采样值更新待求解的模型参数w、b，下一次以当前的w、b为初值，再次更新w、b，直到梯度降为0，模型参数收敛，或者迭代结束（所以，迭代次数少可能还没收敛就结束了，迭代次数多，可能后期收敛之后的计算变化不大）。

3. 完整代码示例

import numpy as np

# example: y = 2x+3 ( y = wx + b)
# 其中 w b 为待估计参数。

# 计算 loss: 所有采样点的均方误差
def computer_error(b, w, points):
    totalError = 0
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        totalError += (y - (w * x + b)) ** 2

    return totalError / len(points)

# 梯度下降的方式，计算所有点的梯度，然后更新估计参数
# loss = (wx+b-y)^2
# dl/db = 2(wx+b-y)      # 下面对应的是N个点的累计平均值
# dl/dw = 2(wx+b-y) * x
# 更新方式： w' = w - dl/dw * lr
#          b' = b - dl/db * lr
def step_gradient(b_cur, w_cur, points, lr):
    '''
    b_cur: current parameter of model b
    w_cur: current parameter of model w
    points: samples of (x,y)
    lr: learning rate
    '''
    b_gradient = 0
    w_gradient = 0
    N = float(len(points))
    for i in range(len(points)):
        x = points[i, 0]
        y = points[i, 1]
        b_gradient += 2 * (w_cur * x + b_cur - y)
        w_gradient += 2 * (w_cur * x + b_cur - y) * x
    b_gradient /= N
    w_gradient /= N
    b_new = b_cur - b_gradient * lr  # 注意：当梯度减小为0,模型参数自然不再变化，即达到收敛状态。
    w_new = w_cur - w_gradient * lr  # 以二次曲线为例，当梯度大于0时，自变量 w 减去（梯度值*学习率），自变量变小，使梯度值也变小，loss也变小。
                                     # 梯度下降，就体现在这个减号上
    return [b_new, w_new]

# 迭代优化，输出模型参数
def gradient_descent_runner(b_start, w_start, points, lr, iterations):
    b = b_start
    w = w_start
    for i in range(0, iterations):
        b, w = step_gradient(b, w, points, lr) # 注意: 这里b、w下一次的的输入，使用了上一次 b、w 的输出
        # print("> After {0} iterations b = {1}, w = {2}, error = {3}"
        #       .format(i + 1, b, w, computer_error(b, w, points)))

    return [b, w]

def run():
    points = np.genfromtxt("data.csv", delimiter=',')
    learning_rate = 0.01
    b_init = 0
    w_init = 0
    num_iterations = 1000
    print("Starting gradient descent at b = {0}, w = {1}, error = {2}"
          .format(b_init, w_init, computer_error(b_init, w_init, points)))
    print("Running...")
    [b, w] = gradient_descent_runner(b_init, w_init, points, learning_rate, num_iterations)
    print("After {0} iterations b = {1}, w = {2}, error = {3}"
          .format(num_iterations, b, w,
                  computer_error(b, w, points)))

if __name__ == '__main__':
    run()

输出结果：

模拟数据（data.csv）：

-6.57,-10.14
-6.5,-10.24
-6.43,-9.86
-5.66,-8.28
-4.54,-6.76
-3.36,-3.72
-1.75,0.55
-1.01,0.98
0.75,4.5
0.68,4.35
2.27,7.55
3.87,10.77
4.66,12.53
1.1,5.3
2.9,7.8
3.22,9.32
4.22,11.12
-10.91,-17.35

其他

线性回归 Liner Regression：即预测对象y是一个连续的值. 比如 年龄 身高等。上述代码属于线性回归。

逻辑回归 Logistic Regression ：在线性回归的基础上加上一个激活函数（压缩作用）比如把（-无穷，+无穷）变换到（0,1）之间。

分类问题 Classification：比如3个种类，最终三个种类的可能性之和是1, 每一个种类的值的范围是[0,1]。

参考：

深度学习入门_哔哩哔哩_bilibili