目录
1. 引例
例1. 数字三角形最小路径和
代码1_ traverse法
代码2_ 分治法DC
代码3_动态规划DP_记忆化搜索(分治法DC + 记忆化)
代码4_动态规划DP_多重循环(本文重点,重点记忆)
动态规划方法对比:记忆化搜索 对比 多重循环
2. 动态规划的套路
2.1 动态规划的四点要素
2.2 什么情况下使用动态规划?
2.3 什么情况下不使用动态规划?
2.4 面试中常见的动态规划类型
3. 坐标型动态规划
例2. 二维矩形左上到右下最小路径和
例3. 二维矩阵从左上到右下统计共有多少路径
例4. 爬楼梯问题(青蛙跳台阶)
例5. 跳跃游戏 (Jump Game) (重点理解)
例6. 跳跃游戏II (Jump Game II)
例7. 最长上升子序列(重点例题)
4. 单序列动态规划
例8. 分割回文串(二)_将字符串全部分割成回文子串,最少分割几次
例9. 单词拆分(一)_字符串是否可以全部拆分成字典中的单词
5. 双序列动态规划
例10. 找两个字符串的最长公共子序列的长度(LCS)
例11. 编辑距离_将word1变成word2的最少操作(增删改)次数
例12. 不同的子序列_字符串S中找子序列T出现的方案个数
例13. 交叉字符串_判断字符串s3是否由字符串s1和s2交叉构成
6. 其他例题
参考:九章算法 lintocde leetcode 代码随想录carl
还有 算法笔记_面试题_18.动态规划_模板及示例十几道(下)
1. 引例 例1. 数字三角形最小路径和描述:给定一个数字三角形,找到从顶部到底部的最小路径和。每一步可以移动到下面一行的相邻数字上。如果只用额外空间复杂度O(n)O(n)完成,可以获得加分,其中n是数字三角形的总行数。
(来源:109 · 数字三角形leetcode 120. 三角形最小路径和 = lintcode 110 · 最小路径和)
输入:
triangle = [
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]输出:11
解释:从顶到底部的最小路径和为11 ( 2 + 3 + 5 + 1 = 11)。
代码1_ traverse法(DFS深度优先遍历)在递归中,每个节点(x,y)都有2种情况,向“左子节点”走(x+1,y), 向“右子节点”(x+1, y+1)走,在走的时候,当前的和 加上 当前的节点的值求路径和sum, 在最后到达最后一层时,取所有到达最后一层路径和中的最小值。
当然,该方法,由于重复遍历了很多节点,所以可能超时。
class Solution {
public:
/**
* @param triangle: a list of lists of integers
* @return: An integer, minimum path sum
*/
int result;
int minimumTotal(vector &triangle) {
// write your code here
result = INT_MAX;
int sum = 0;
traverse(0, 0, sum, triangle);
return result;
}
void traverse(int x, int y, int sum, vector & A) {
if (x == A.size()){ //注意:退出条件,到达最后一层
if (sum < result) {
result = sum;
}
return;
}
traverse(x + 1, y , sum + A[x][y], A); // 向下走(类似左子节点)
traverse(x + 1, y + 1, sum + A[x][y], A); // 向下向右走(类似右子节点)
}
};traverse方法的时间复杂度:O(2^n),因为每次进入循环都有两条路径,又因为总共有n层,所以是2^n次。(n代表的是数字三角形的层数)
代码2_ 分治法DC(DFS深度优先遍历)分治法有返回值。
返回值:在最下面的一层的下一层(类似于空节点)返回0。
单层的处理方法:在当前层 直接返回 “左右子树”中最小的值 与 当前节点的值 的和。即假设下面的每一层都计算好了(子问题的解有了),直接 加上 当前层的值即可。
class Solution {
public:
int minimumTotal(vector &triangle) {
// write your code here
int result = divideConquer(0, 0, triangle);
return result;
}
int divideConquer(int x, int y, vector & A) {
if (x == A.size()){ //注意:最后一层的下一层时(相当于空节点)的返回值
return 0;
}
return A[x][y] + min(divideConquer(x + 1, y, A),
divideConquer(x + 1, y + 1, A));
}
};分治法的时间复杂度是O(n^2) , 因为每层n个节点,总共n层,每个点访问一次,访问了所有的节点,所以是 = n*( n-1)/2 = n^2 。(n代表的是数字三角形的层数)
代码3_动态规划DP_记忆化搜索(分治法DC + 记忆化)考虑到在下面每层计算时有重复计算的路径,所以,这种方法作了优化,定义一个dp数组dp[x][y], 表示从当前层节点(x,y)到最下面一层的某一节点的最短路径值,若该值已经计算过了(留意下面代码中的判断方式),则直接返回即可,不必重复计算(动态规划和分治法的重要区别)。比如下面的e点对应路径e-h子路径,就被蓝色路径和青色路径计算多次。(递归:所以是自下而上)

class Solution {
public:
int minimumTotal(vector &triangle) {
// write your code here
int N = triangle.size();
vector dp(N, vector(N, INT_MAX)); //特别注意: 该dp[x][y]代表的含义:从当前节点(x,y)到最下面一层某节点的最小路径和,即子问题的解。
int result = divideConquer(0, 0, triangle, dp);
return result;
}
int divideConquer(int x, int y, vector & A, vector& dp) {
if (x == A.size()){ //注意:最后一层的下一层时(相当于空节点)的返回值
return 0;
}
if (dp[x][y] != INT_MAX) { //如果当前节点的最路径和计算过了,直接返回即可,避免重复计算,这里体现记忆化搜索。
return dp[x][y];
}
dp[x][y] = A[x][y] + min(divideConquer(x + 1, y, A, dp), //相当于“左子节点”
divideConquer(x + 1, y + 1, A, dp));//相当于“右子节点”
return dp[x][y];
}
};那典型的动态规划是怎么做的呢?有2种方式,自上而下或者自下而上(两者差不多)。我们统一使用自上而下的方式。
动态规划解题思路:
递推公式:定义dp数组 f[x][y], 表示从最顶层到当前节点时的所有路径和中的最小者。则当前节点的取值 = 当前节点的值 + 上面两个节点中的较小者。即 f[x][y] = A[x][y] + min( f[x-1][y-1], f[x-1][y]
(比如h节点的dp值= h节点的值 + min(d节点的dp值,e节点的dp值))

初始化: 因为是自上而下计算dp数组,所有数字三角形的边缘节点没有2个节点中去选择,就是上一个节点的dp值 + 当前节点的值。所以要对边缘的节点进行初始化(图中红色节点)。
返回值: 自上而下,到达最底一层,则最底一层的dp就是所有的候选最小值集合,最小值即为最低一层中dp值中的最小者。
class Solution {
public:
int minimumTotal(vector& triangle) {
int N = triangle.size();
vector dp(N, vector(N,INT_MAX)); //定义动态规划数组:dp[x][y], 表示从最顶层到当前节点时的所有路径和中的最小者
//初始化
dp[0][0] = triangle[0][0];
for(int i = 1; i < N; ++i) {
dp[i][0] = triangle[i][0] + dp[i-1][0];
dp[i][i] = triangle[i][i] + dp[i-1][i-1];
}
// 动态规划自上而下
for(int i = 2; i < N; ++i) { //从 1开始也可以(dp[0][1]无对应的意义),不过从2开始更合适。因为初始化之后第一个待求dp是dp[2][1]
for(int j = 1; j < i; ++j) {
dp[i][j] = triangle[i][j] + min(dp[i-1][j-1], dp[i-1][j]);
}
}
int result = INT_MAX;
for (int i = 0; i < N; ++i) {
result = min(result, dp[N-1][i]);
}
return result;
}
};
- 状态 State
- 灵感,创造力,存储小规模问题的结果
- 方程 Function
- 状态之间的联系,怎么通过小的(或前一个)状态来算大的(后一个)状态
- 初始化 Initialization
- 最极限的小状态是什么, 起点
- 答案 Answer
- 最大的那个状态是什么,终点
动规要使用到 “状态”,状态必须要定义的清清楚楚明明白白;对于递归,函数的签名就是“状态”,对于动规,比如数字三角形,f[i][j]就是状态(接受什么参数,自身代表(返回)什么值)。
有了状态之后,再去研究“状态”和“状态”之间的关系,比如递推关系。。。(比如 访问根节点时的状态,跟访问左右子树时的状态之间时什么关系)
2.2 什么情况下使用动态规划?- 求最大值最小值
- 判断是否可行
- 统计方案个数
- 求出所有 具体 的方案而非方案 个数 http://www.lintcode.com/problem/palindrome-partitioning/
- 输入数据是一个 集合 而不是 序列http://www.lintcode.com/problem/longest-consecutive-sequence/
- 坐标型动态规划 15%
- 序列型动态规划 30%
- 双序列动态规划 30%
- 划分型动态规划 10%
- 背包型动态规划 10%
- 区间型动态规划 5%
思路模板:(记住,若能表示成有一个小人在坐标上跳时。)

f[x] 表示从起点走到坐标x时的***(索引为x, 索引一般都是从0开始的)。
九章算法:初始化一个二维的动态规划时,就去初始化第0行和第0列。
例2. 二维矩形左上到右下最小路径和描述:给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。说明:一个机器人每次只能向下或者向右移动一步。(来源:leetcode 剑指 Offer II 099. 最小路径之和 = lintcode 110 · 最小路径和)
示例:
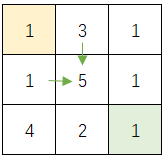
输入:grid = [[1,3,1],[1,5,1],[4,2,1]] 输出:7 解释:因为路径 1→3→1→1→1 的总和最小。
代码
同数字三角形一样。类似的,当前位置(x,y)的状态,是由正上方(x-1, y)的状态,和左侧位置(x, y-1)的状态决定的。只不过返回值只有一个候选值(右下角的dp值)。
状态的定义:运行到当前位置(x,y)时的最小路径和。
class Solution {
public:
int minPathSum(vector& grid) {
if (grid.size() == 0) {
return -1;
}
int m = grid.size();
int n = grid[0].size();
vector dp(m, vector(n));
// initialization
dp[0][0] = grid[0][0];
for(int i = 1; i < m; ++i) {
dp[i][0] = dp[i-1][0] + grid[i][0]; // 第一列的状态,只由上方状态决定
}
for(int i = 1; i < n; ++i) {
dp[0][i] = dp[0][i-1] + grid[0][i]; // 第一行的状态,只由左侧状态决定
}
// dynamic programming
for (int i = 1; i < m; ++i) { // 其他位置的状态,由上方+左侧的状态共同决定
for (int j = 1; j < n; ++j) {
dp[i][j] = grid[i][j] + min(dp[i-1][j], dp[i][j-1]);
}
}
// get result
return dp[m-1][n-1];
}
};描述:一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。问总共有多少条不同的路径?(来源: leetcode 62. 不同路径 = lintcode 114 · 不同的路径)
示例 :
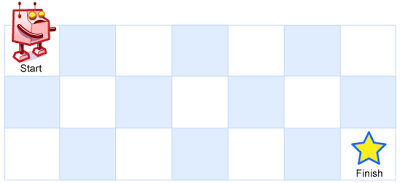
输入:m = 3, n = 7 输出:28
代码
类似例2,dp数组(状态数组)含义一致。不同在于,当前状态(当前路径总数)等于 上侧与左侧状态之和。
class Solution {
public:
int uniquePaths(int m, int n) {
vector dp(m, vector(n)); //dp数组含义: 到达当前位置时,总共的路径条数
for (int i = 0; i < m; ++i) { // 初始化第一行第一列
dp[i][0] = 1;
}
for (int i = 0; i < n; ++i) {
dp[0][i] = 1;
}
for (int i = 1; i < m; ++i) { // 动态规划:当前状态等于上方状态加右方状态
for (int j = 1; j < n; ++j) {
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
}
};描述:假设你正在爬楼梯,需要n步(台阶总数)你才能到达顶部。但每次你只能爬一步或者两步,爬到顶部的方法有多少种?(来源:lintcode 111 · 爬楼梯 = leetcode剑指 Offer 10- II. 青蛙跳台阶问题)

样例1:
输入:3 输出:3
解释:1, 1, 1; 1, 2; 2, 1 共3种
样例2:
输入:1 输出:1
解释:只有一种方案
class Solution {
public:
int climbStairs(int n) {
if (n 1 -> 4(这里的数字为下标)是一种合理的方案。
代码
当前的位置是否能够达到,取决于前面的位置是否能够达到。若前面的位置能够达到,且 能够达到的位置的索引 + 所在位置的值 >= 当前位置的索引,则当前位置也能达到(即 dp[i] = true, 当 dp[j] +j >= i时, j属于[0, i)之间)。为什么是大于等于?因为每个元素代表在那个位置可以跳跃的最大长度。(注意:找到一次true之后就可以且应该返回)。
注意:这里定义的dp数组是一个bool数组,dp[i]表示能否到达索引为i的位置。另外遍历的循环是2层,所以时间复杂度是O(n^2)。
class Solution {
public:
bool canJump(vector &A) {
int N = A.size();
if (N = i) { //每个元素代表你在那个位置可以跳跃的最大长度,所以>=即可,不需要严格等于
dp[i] = true;
break;
}
}
}
return dp[N-1];
}
};
数组A的长度不超过20000,每个元素的大小不超过20000
样例
输入:A = [2,3,1,1,4]
输出:2
解释:到达最后位置的最小跳跃次数是2(从下标0到1跳跃1个距离长度,然后跳跃3个距离长度到最后位置)
代码
类似例5跳跃游戏。只不过,这里状态dp[i]表示的含义是,到达索引为i的位置所需要的最小跳跃次数。递推公式:当前位置的状态(最小跳跃次数)等于前面位置上的状态(前面的可以1步跳到当前状态的候选状态集合) + 1 中 的最小值。不要忘了前提:上一个状态可以到达。
class Solution {
public:
int jump(vector &A) {
int N = A.size();
vector dp(N, INT_MAX); //dp[i]表示跳到索引为i的位置需要的最小跳跃次数 //特别注意:取最小值,所以这里采用INT_MAX初始化
dp[0] = 0;
for (int i = 1; i < N; ++i) {
for (int j = 0; j < i; ++j){
if (dp[j] != INT_MAX && A[j] + j >= i){ //条件:索引为j的节点可以到达,且从j节点可以到达i时,
dp[i] = min(dp[i], dp[j] + 1); //取所有可达到方案中跳跃次数最小的
}
}
}
return dp[N-1];
}
};描述:给定一个整数序列,找到最长上升子序列(LIS),返回LIS的长度。
最长上升子序列的定义:最长上升子序列问题是在一个无序的给定序列中找到一个尽可能长的由低到高排列的子序列,这种子序列不一定是连续的或者唯一的。
(来源:lintcode 76 · 最长上升子序列 =leecode 300. 最长递增子序列)
样例
输入:nums = [5,4,1,2,3] 输出:3 解释:LIS 是 [1,2,3]
代码
定义状态: dp[i] 表示索引为i的位置时(从起点走到索引为i的位置,以 i 结尾时的)的最长子序列的值
状态转移: dp[i] = max(dp[i], dp[j] + 1) 当 j < i, 且 nums[j] < nums[i] 时。
当前状态 等于 前面状态中可以连接到(上一个状态的nums小于当前状态的nums)当前状态的那些状态 + 1(连接到当前位置长度,所以加1)中取值最小的。
class Solution {
public:
int longestIncreasingSubsequence(vector &nums) {
int N = nums.size();
if (N == 0) {
return 0;
}
vector dp(N, 1);
for(int i = 1; i < N; ++i) {
for (int j = 0; j < i; ++j) {
if (nums[j] < nums[i]) { //注意:对比对象
dp[i] = max(dp[i], dp[j] + 1);
}
}
}
int result = INT_MIN;
for(int i = 0; i < N; ++i) {
result = max(result, dp[i]); //注意:这里 max中对比的是谁!!!
}
return result;
}
};时间复杂度: 因为两层循环,所以是O(n^2)。
其他题目:
lintcode :

思路模板:

描述:给定字符串 s, 需要将它分割成一些子串, 使得每个子串都是回文串. 最少需要分割几次?(来源: leetcode 132. 分割回文串 II (级别:困难) = lintcode 108 · 分割回文串(二))
样例 1:
- 输入:s = "a"
- 输出:0
- 解释:"a" 本身就是回文串, 无需分割
样例 2:
- 输入:s = "aab"
- 输出:1
- 解释:将 "aab" 分割一次, 得到 "aa" 和 "b", 它们都是回文串.
代码
状态定义: dp[i]表示前i个字符串分割成回文串,最少需要分割的次数。
状态转移:对于前i个子串, 若之前的状态比如dp[j]的值, 以及 子串 [ j , i-1 ] 是否是回文串,决定了前i个子串的状态的值,即若子串[j, i-1]是回文,则dp[j] 再切一刀就保证了每个子串都是回文串,则dp[i] = dp[j]+1。 在这些状态中选最小的即可(单序列动态规划)。总而言之,
- dp[i] = min(dp[i], dp[j] + 1), 在条件子串[j, i-1]是回文时。

判断一个string中的所有子串是否是回文串,也是动态规划(区间型动态规划)。使用一个二维bool数组记录所有子串是否是回文,状态dp[i][j]表示s的子串[i,j]是否是回文。状态转移方程:
- dp[i][j] = dp[i+1][j-1] && (s[i] == s[j])
- 即对于当前子串[i,j], 只有当两头相等,中间是true时,当前为true.

class Solution {
public:
int minCut(string &s) {
// write your code here
int N = s.size();
if (N inention (删除 't') inention -> enention (替换 'i' 为 'e') enention -> exention (替换 'n' 为 'x') exention -> exection (替换 'n' 为 'c') exection -> execution (插入 'u')
代码
状态定义:跟上一题 (例10) 基本上一样,换汤不换药。定义二维数组维度[N1+1, N2+1], dp[i][j]表示:word1的前i个字符变换到word2的前j个字符最少操作次数。则状态dp[i-1][j-1]到dp[i][j]中间需要判断的字符对是word1[i-1] 和word2[j-1] (注意这里是-1, i j在状态中表示前i或前j,当作索引使用时,表示索引位置时要留意下是否-1) 则:
状态转移:这两字符对相等时,三种情况:a.当前状态编辑距离等于上一状态的编辑距离(dp[i][j] = dp[i-1][j-1]),b. 或者当前状态word1中一个字符忽略该字符(word1[i-1])的状态dp[i-1][j]增加一个字符(即dp[i][j] = dp[i-1][j] + 1),c. 或者当前状态忽略word2[j-1] 删除一个字符(即dp[i][j] = dp[i][j-1] + 1),三者取最小。
这两字符对不相等时: a. 变换成相等的,即上一个状态加一次变换操作(dp[i][j] = dp[i-1][j-1] + 1); b. 同相等时的情况b; c.同相等时的情况c。
初始化:dp[i][0] 表示 word1中前i个字符变换到word2中前0个字符的最小变换次数,显然需要i次删除操作,所以是dp[i][0] = i; 同理 dp[0][j] = j。
class Solution {
public:
int minDistance(string &word1, string &word2) {
int N1 = word1.size();
int N2 = word2.size();
vector dp(N1 + 1, vector(N2 + 1));
for (int i = 0; i < N1 + 1; i++) {
dp[i][0] = i;
}
for (int i = 1; i < N2 + 1; i++) { //最好从1开始,[0][0]已赋值
dp[0][i] = i;
}
for (int i = 1; i < N1 + 1; i++) {
for (int j = 1; j < N2 + 1; j++) {
if (word1[i-1] == word2[j-1]) { //特别注意:这里判断的是 i-1 和 j-1 对应的字符是否相等!
dp[i][j] = min(dp[i-1][j-1], min(dp[i-1][j]+1, dp[i][j-1]+1)); //注意:三种情况(不用动,删i-1,加j-1)
} else {
dp[i][j] = min(dp[i-1][j-1]+1, min(dp[i-1][j]+1, dp[i][j-1]+1)); //注意:三种情况(改,删i-1,加j-1)
}
}
}
return dp[N1][N2];
}
};
例12. 不同的子序列_字符串S中找子序列T出现的方案个数
描述:给定字符串 S 和 T, 字符串S中有多少个子序列字符串和字符串T相同。 子序列字符串是原始字符串删除一些(或零个)字符之后得到的字符串, 并且不能改变剩下字符的相对位置。(比如 "ACE" 是 ABCDE 的一个子序列, 而 "AEC" 不是) (来源:lintcode 118 · 不同的子序列 (中等)= leetcode 115. 不同的子序列 (困难))样例 1:
- 输入:S = "rabbbit" T = "rabbit" 输出:3
- 解释:你可以删除 S 中的任意一个 'b', 所以一共有 3 种方式得到 T.
样例 2:
- 输入:S = "abcd" T = "" 输出:1
- 解释:只有删除 S 中的所有字符这一种方式得到 T
代码
状态定义:dp[i][j]表示从S中的前i个字符中选择(j个字符)等于T中前j个字符的方案有多少个。
状态转移:当前状态dp[i][j];上一个状态dp[i-1][j-1], 相关状态 dp[i-1][j];对应的要判断的字符对是S[i-1] 和 T[j-1]。
当这两个字符相等时,有两种情况,一种情况是使用这两个字符,且从S中i-1前面选择j-1个字符,匹配T中前j-1个字符,共同组成T中的前j字符串即状态 + dp[i-1][j-1];另一种情况是,虽然相等,但也可能使用S中的前i-1中(放弃选择S[i-1])直接选择j个字符,跟T中的前j个字符进行匹配, 即 + dp[i-1][j]. 所以 dp[i][j] = dp[i-1][j-1] + dp[i-1][j].
当两个字符不相等时,只有一种情况,只能从S中的前i-1中(不能选择S[i-1])直接选择j个字符跟T中的前j个字符进行匹配,即 dp[i][j] = dp[i-1][j].
初始化:初始化的是二维状态数组的第1列 和第1行,一定要明确好状态的定义。dp[i][0]表示S中前i个选择0个子串等于T中前0个子串有几种方案,显然是1。dp[0][j]根据状态定义显然是0。
class Solution {
public:
int numDistinct(string &S, string &T) {
int N1 = S.size();
int N2 = T.size();
vector dp(N1 + 1, vector(N2 + 1));// dp[i][j]表示从S中的前i个字符中选取等于T中前j个字符的方案有多少个
for (int i = 0; i < N1 + 1; i++) {
dp[i][0] = 1; //从S前i个选择等于T中前0个字符串(即空串)的方案只有1种,即S前i个中选择0个。
}
for (int j = 1; j < N2 + 1; j++) {// 特别注意:这里从1开始,因为dp[0][0]=1, dp[0][j]=0
dp[0][j] = 0; //从S前0个选择等于T中前j个字符串的子串 的方案有0种。
}
for (int i = 1; i < N1 + 1; i++) {
for (int j = 1; j < N2 + 1; j++) {
if (S[i-1] == T[j-1]) {
dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
} else {
dp[i][j] = dp[i-1][j];
}
}
}
return dp[N1][N2];
}
};
例13. 交叉字符串_判断字符串s3是否由字符串s1和s2交叉构成
描述:给出三个字符串s1、s2、s3,判断s3是否由s1和s2交叉构成。(来源:lintcode 29 · 交叉字符串 (困难) = leetcode 剑指 Offer II 096. 字符串交织 (中等))样例 1:
- 输入:
- s1 = "aabcc"
- s2 = "dbbca"
- s3 = "aadbbcbcac"
- 输出:true
- 解释:s3 是由 s1 与 s2 交叉构成。
样例 2:
- 输入:s1 = "" s2 = "" s3 = "1"
- 输出:false
- 解释:s3 不是由 s1 与 s2 交叉构成。
代码
状态定义:dp[i][j]表示从s1中选择前i个和从s2中选择前j个是否能组成s3中前i+j个字符。
状态转移:当前状态由两种情况转移过来,一种是s1中选i-1个,s2中选择j个的状态dp[i-1][j]转移过来的,这时需要判断s3中当前状态的最后一个字符(索引为i+j-1)是否来自于s1中的索引为i-1的字符(转移状态时的字符s1[i-1])。
另一种情况状态dp[i][j-1]同理(转移状态时的字符s2[j-1])。这两种情况一起决定了当前状态。
初始化:这个初始化稍微有点繁琐(请时刻牢记状态的定义)。初始化对象,依然还是二维状态数组的第一列和第一行,如第1列的初始化dp[i][0] 表示从s1中选择前i个,s2中选择前0个,组成s3中前i+0个的状态,所有该状态由s1前i个字符是否全都等于s3前i+0个字符决定。即 dp[i][0] = dp[i-1][0] && (s1[i-1] == s3[i-1]) 。所以这里先初始化了 dp[0][0]=true (0+0=0显然合理)。
class Solution {
public:
bool isInterleave(string s1, string s2, string s3) {
int N1 = s1.size();
int N2 = s2.size();
int N3 = s3.size();
if (N1 + N2 != N3) {
return false;
}
vector dp(N1 + 1, vector(N2 + 1)); //dp[i][j]表示从s1中选择前i个和从s2中选择前j个是否能组成s3中前i+j个字符。
//初始化
dp[0][0] = true;
for (int i = 1; i < N1 + 1; i++) { //从s1中选择前i个,s2中选择前0个,组成s3中前i+0个的状态,由s1前i个字符是否全都等于s3前i+0个字符决定。
dp[i][0] = dp[i-1][0] && (s1[i-1] == s3[i-1]);
}
for (int j = 1; j < N2 + 1; j++) {
dp[0][j] = dp[0][j-1] && (s2[j-1] == s3[j-1]);
}
//状态转移
for (int i = 1; i < N1 + 1; i++) {
for (int j = 1; j < N2 + 1; j++) { //当前状态由两种情况转移过来,一种是s1中选i-1个,s2中选择j个的状态dp[i-1][j]转移过来的,这时需要判断s3中当前状态的最后一个字符(索引为i+j-1)是否来自于s1中的索引为i-1的字符(转移状态时的字符)。另一种情况同理。
dp[i][j] = (dp[i-1][j] && (s1[i-1] == s3[i+j-1]))
||(dp[i][j-1] && (s2[j-1] == s3[i+j-1]));
}
}
return dp[N1][N2];
}
};
6. 其他例题
背包
类
:
http://www.lintcode.com/problem/backpack/
http://www.lintcode.com/problem/backpack-ii/
http://www.lintcode.com/problem/minimum-adjustment-cost/
http://www.lintcode.com/problem/k-sum/
区
间类
:
http://www.lintcode.com/problem/coins-in-a-line-iii/
http://www.lintcode.com/problem/scramble-string/ (hard)
划分
类
:
http://www.lintcode.com/problem/best-time-to-buy-and-sell-stock-iv/ (hard)
http://www.lintcode.com/problem/maximum-subarray-iii/



