C++_数据结构_堆用法详解

目录

1. 基本概念

1.1 树存储结构

1.2 priority_queue 优先队列

2. 创建堆

3. 堆操作

3.1 插入 push_back() + std::push_heap()

3.2 弹出  std::pop_heap() + pop_back()

3.3 检查序列是否是堆 std::is_heap() 或者 std::is_heap_until()

3.4 将元素段作为堆来排序 std::sort_heap()

3.5 用堆作为优先级队列

1. 基本概念

堆（heaps）是一种特殊的数据组织方式，STL 中的 priority_queue 容器适配器底层就是采用堆来组织数据存储的。为了弄明白堆是什么，首先要搞清楚什么是树存储结构。

1.1 树存储结构

树是分层排列的元素或节点。每个节点有一个键，它是节点中所保存的对象，就如同链表中的节点。父节点是有一个或两个子节点的节点。一般父节点可以有任意个数的子节点，树中的父节点不需要有相同个数的子节点。没有子节点的节点叫作叶节点。一般父节点的键与其子节点有一些关系。树都有一个根节点，它是树的基础，从根节点可以到达所有的子节点。

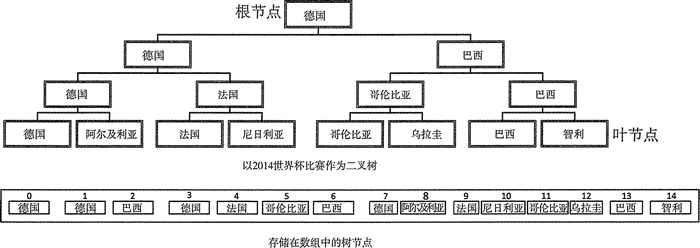
图 1 二叉树示例

图 1 展示了一棵树，它表示 2014 年世界杯最后一组比赛的结果。德国全部赢了，所以它是根节点；它在最后一场比赛中打败了巴西队，所以它和巴西队是它自己的子节点。每个父节点最多有两个子节点的树叫作二叉树。 图 1 中的树是一个完全二叉树，因为每个父节点都有两个子节点。任何树的父节点都有指向子节点的指针。完全二叉树可以用数组的方式保存，也可以用其他顺序表的方式保存，例如 vector，这样就不需要保存子节点的指针，因为知道每一层节点的编号。 如果将每一层树的层数记作 n，从根节点开始作为第 0 层，每一层包含 2n 个节点。图 1 展示了世界杯比赛树的节点如何存储在数组中。每个节点上的整数值是索引值。根节点存放在数组的第一个元素中，后面是它的两个子节点。这对子节点的孩子节点出现在序列的下个位置，以此类推直到叶节点。子节点的索引值为 n,那么它的父节点的索引值就为 (n-1)/2。如果数组元素从 1 开始索引，那么父节点的索引表达式更加简单，它为 n/2。 现在可以定义一个堆：这个堆是一个完全二叉树，每个节点与其子节点位置相对。父节点总是大于或等于子节点，这种情况下被叫作大顶堆，或者父节点总是小于或等于子节点，这种情况下叫作小顶堆。注意，给定父节点的子节点不一定按顺序排列。

1.2 priority_queue 优先队列

priority_queue 逻辑上使用堆结构（完全二叉树）实现，物理上（默认）使用动态数组实现，并非完全有序，但是如果按照指定方式出队，结果可以是有序的。

它总是先输出根节点的值，然后调整树使之继续成为一棵完全二叉树 ，每次输出的根节点总是整棵树优先级最高的，要么数值最小要么数值最大。

它是一种内部不完全有序的结构，但每次若返回的都是top,然后pop(完全二叉树的根节点，pop完后自动调整，保存堆的结构和性质)，是可以有序输出的。

内部实现：

template 
class priority_queue
{
    // ...
protected:
    //  See queue::c for notes on these names.
    _Sequence c;
    _Compare comp;

public:
    explicit priority_queue(const _Compare &__x, const _Sequence &__s)
        : c(__s), comp(__x)
    {
        std::make_heap(c.begin(), c.end(), comp);
    }

    explicit priority_queue(const _Compare &__x, _Sequence &&__s = _Sequence())
        : c(std::move(__s)), comp(__x)
    {
        std::make_heap(c.begin(), c.end(), comp);
    }

    // ...

    const_reference
    top() const
    {
        __glibcxx_requires_nonempty();
        return c.front();
    }

    void
    push(const value_type &__x)
    {
        c.push_back(__x);
        std::push_heap(c.begin(), c.end(), comp);
    }

    void
    pop()
    {
        __glibcxx_requires_nonempty();
        std::pop_heap(c.begin(), c.end(), comp);
        c.pop_back();
    }
    
    // ...
}

2. 创建堆

用来创建堆的函数定义在头文件 中。max_heap() 对随机访问迭代器指定的一段元素重新排列，生成一个堆。默认使用的是 < 运算符，可以生成一个大顶堆。例如：

std::vectornumbers{2.5,10.0,3.5,6.5,8.0,12.0,1.5,6.0};
std::make_heap(std::begin(numbers), std::end(numbers));//{12 10 3.5 6.5 8 2.5 1.5 6}

调用 make_heap() 后，vector 中的元素如注释所示，这也说明了图 2 所展示的结构。

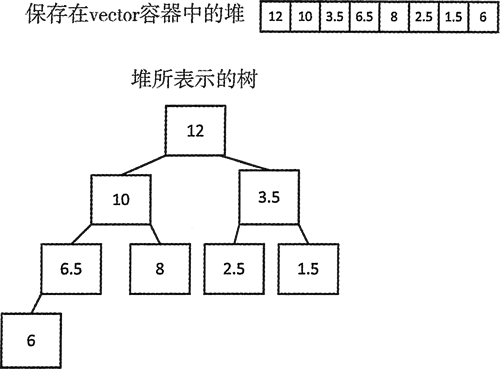
图 2 堆所表示的树

根节点是 12，10 和 3.5 是它的子节点。10 的子节点是 6.5 和 8，3.5 的子节点是 2.5 和 1.5。6.5 只有一个叶节点 6。 priority_queue 是一个堆。在底层，一个 priority_queue 实例创建了一个堆。在堆中，所有成对的连续元素不需要有相同的比较关系。图 2 所示堆中的前 3 个元素是顺序递减的，但第 4 个元素却大于第 3 个元素。既然如此，为什么 STL 有 priority_queue (它是一个堆)，却还需要创建堆，特别是还需要将堆作为优先级队列？ 这是因为 priority_queue 可以提供堆没有的优势，它可以自动保持元素的顺序；但我们不能打乱 priority_queue 的有序状态，因为除了第一个元素，我们无法直接访问它的其他元素。如果需要的是一个优先级队列，这一点非常有用。 从另一方面来说，使用 make_heap() 创建的堆可以提供一些 priority_queue 没有的优势：

1. 可以访问堆中的任意元素，而不限于最大的元素，因为元素被存储在一个容器中，就像是我们自己的 vector。这也提供了偶然破坏元素顺序的可能，但是总可以调用 make_heap() 来还原堆。
2. 可以在任何提供随机访问迭代器的序列容器中创建堆。这些序列容器包括普通数组、string 对象、自定义容器。这意味着无论什么时候需要，都可以用这些序列容器的元素创建堆，必要时，可以反复创建。甚至还可以为元素的子集创建堆。

如果使用保持堆顺序的函数，那么可以将堆当作优先级队列使用。 这里有另一个版本的 make_heap()，它有第 3 个参数，可以用来指定一个比较函数用于堆的排序。通过定义一个大于运算符函数，可以生成一个小顶堆。这里可以使用 functional 中的断言。例如：

std::vector numbers {2.5, 10.0, 3.5, 6.5, 8.0, 12.0, 1.5, 6.0};
std::make_heap(std::begin(numbers), std::end(numbers), std::greater()); //{1.5 6 2.5 6.5 8 12 3.5 10}

可以将模板类型参数指定为 greater。这里的这个尖括号为空的版本推断并返回了类型参数。已经有一个用 make_heap() 函数在容器中生成的堆。可以在它上面进行很多操作，下面我们来深入了解这些操作。

3. 堆操作

堆不是容器，而是组织容器元素的一种特别方式。只能确定堆的范围，即开始和结束迭代器指定的范围。这意味着可以用容器中的元素子序列创建堆。可以在已生成的堆中添加元素。

3.1 插入 push_back() + std::push_heap()

乍一看，algorithm 中的函数模板 push_heap() 创建堆的方式可能会觉得有些奇怪。为了向堆中添加元素，首先可以用任何方法将元素附加到序列中。然后调用 push_heap() 来插入最后一个元素，为了保持堆的结构，这个元素会被重新排列到一个适当的位置。

std::vector numbers {2.5, 10.0, 3.5, 6.5, 8.0, 12.0, 1.5, 6.0};
std::make_heap(std::begin(numbers),std::end(numbers));//{12 10 3.5 6.5 8 2.5 1.5 6}
numbers.push_back(11); // {12 10 3.5 6.5 8 2.5 1.5 6 11}
std::push_heap(std::begin(numbers), std::end(numbers));//{12 11 3.5 10 8 2.5 1.5 6 6.5}

注释显示了每个操作执行后的效果。必须以这种方式向堆中添加元素。只能通过调用成员函数向 queue 中添加新元素，而且这个成员函数只接受迭代器作为参数，不能直接以元素作为参数。 push_back() 会在序列末尾添加元素，然后使用 push_heap() 恢复堆的排序。通过调用 push_heap()，释放了一个信号，指出我们向堆中添加了一个元素，这可能会导致堆排序的混乱。push_heap() 会因此认为最后一个元素是新元素，为了保持堆结构，会重新排列序列。 从上面这个示例可以看出，重新排列是有必要的。我们注意到，尽管这个序列是一个堆，但是它的元素并不完全是按降序排列。这清楚地表明，尽管优先级队列是一个堆，但堆元素的顺序并不一定要和优先级队列相同。 当然，也可以用自己的比较函数来创建堆，但是必须和 push_heap() 使用相同的比较函数：

std::vector numbers {2.5, 10.0, 3.5, 6.5, 8.0, 12.0, 1.5, 6.0};
std::make_heap(std::begin(numbers), std::end(numbers), std::greater());//{1.5 6 2.5 6.5 8 12 3.5 10}
numbers.push_back(1.2);//{1.5 6 2.5 6.5 8 12 3.5 10 1.2}
std::push_heap(std::begin(numbers), std::end(numbers),std::greater());//{1.2 1.5 2.5 6 8 12 3.5 10 6.5}

如果 push_heap() 和 make_heap() 的第 3 个参数不同，代码就无法正常执行。注释显示的结果中，最后的 6.5 似乎有些奇怪，图 3 展示的堆树能说明这个问题。

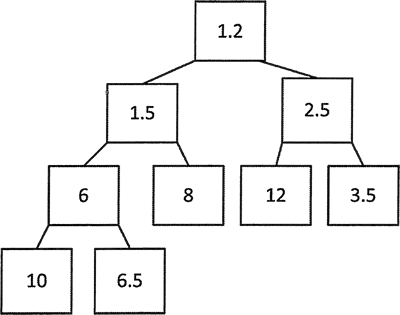
图3 浮点值数堆

从树来看，显然 6.5 是 6（而不是 10）的子节点，所以这个堆结构是正确的。

3.2 弹出  std::pop_heap() + pop_back()

删除最大元素和添加元素到堆的过程有些相似，但所做的事是相反的。首先调用 pop_heap()，然后从容器中移除最大的元素，例如：

std::vector numbers{2.5, 10.0, 3.5, 6.5, 8.0, 12.0, 1.5, 6.0};
std::make_heap(std::begin(numbers),std::end(numbers));//{12 10 3.5 6.5 8 2.5 1.5 6}
std::pop_heap(std::begin(numbers),std::end(numbers));//{10 8 3.5 6.5 6 2.5 1.5 12}
numbers.pop_back();//{10 8 3.5 6.5 6 2.5 1.5}

pop_heap() 函数将第一个元素移到最后，并保证剩下的元素仍然是一个堆。然后就可以使用 vector 的成员函数 pop_back() 移除最后一个元素。如果 make_heap() 中用的是自己的比较函数，那么 pop_heap() 的第 3 个参数也需要是这个函数：

std::vector numbers {2.5, 10.0, 3.5, 6.5, 8.0, 12.0, 1.5, 6.0};
std::make_heap(std::begin(numbers),std::end(numbers),std::greater());//{1.5 6 2.5 6.5 8 12 3.5 10}
std::pop_heap(std::begin(numbers), std::end(numbers),std:: greater());//{2.5 6 3.5 6.5 8 12 10 1.5}
numbers.pop_back();//{2.5 6 3.5 6.5 8 12 10}

从注释显示的操作结果来看，显然需要为 pop_heap() 提供一个比较运算符函数。pop_heap() 函数不会交换第一个元素和最后一个元素，它会对从 begin(numbers) 到 end(numbers)-1 这个范围内的元素重新排序，从而保持堆的顺序。为了能够正确执行这个操作，pop_heap() 必须和make_heap() 使用相同的比较函数。

3.3 检查序列是否是堆 std::is_heap() 或者 std::is_heap_until()

因为可能会打乱容器中的堆，所以 STL 提供了一个检查序列是否仍然是堆的方法：

if(std::is_heap(std::begin(numbers),std::end(numbers)))
std::cout