参考课程:中国大学MOOC《网络安全》——北京航空航天大学
- 网络安全笔记3——双钥密码体制
- Diffie-Hellman公钥密码思想
- 理论基础
- 公钥加密方案
- 公钥密码体制的特点
- 公钥密码体制的用途
- 公钥密码体制的安全性
- RSA密码体制
-
- 算法说明
- 算法使用及特点
- 算法实例
- 算法安全性
- ElGamal密码体制
-
- 算法说明
- Diffie-Hellman公钥密码体制
-
- 密钥交换过程
- 实例
- 协议的安全性
- 椭圆曲线密码体制(ECC)
-
- 优势
- 实数域上椭圆曲线的概念
- 实数域椭圆曲线上加法
- 有限域Ep(a, b)上的椭圆曲线
-
- 举例说明——E23(1,1)的椭圆曲线
- 有限域Ep(a,b)上的椭圆曲线结论
- 有限域Ep(a,b)上的椭圆曲线的性质
- 建立在椭圆曲线上的密码
-
- 椭圆曲线上的Diffie- Hellman密钥交换
- 椭圆曲线公钥加密/解密算法
- RSA算法与ECC算法比较
- 中国商用密码SM2算法
-
- SM2推荐使用的椭圆曲线参数
- SM2加解密算法涉及的辅助函数
- 密钥生成
- SM2加密算法
- SM2解密算法
- 公钥算法总结
●1976年,美国斯坦福大学电气工程系的研究员Diffie和Hellman教授在奠基性论文“密码学的新方向”中提出公开密钥密码体制的概念,旨在解决网络通信的两大安全问题:保密与认证。 ●公钥密码体制的基础,是计算复杂度理论(对称密码体制的基础是混淆和扩散)。其安全性主要取决于构造算法所依赖的数学难题。 单向函数/单向陷门函数 计算上困难问题/NP完全问题
Diffie-Hellman公钥密码思想
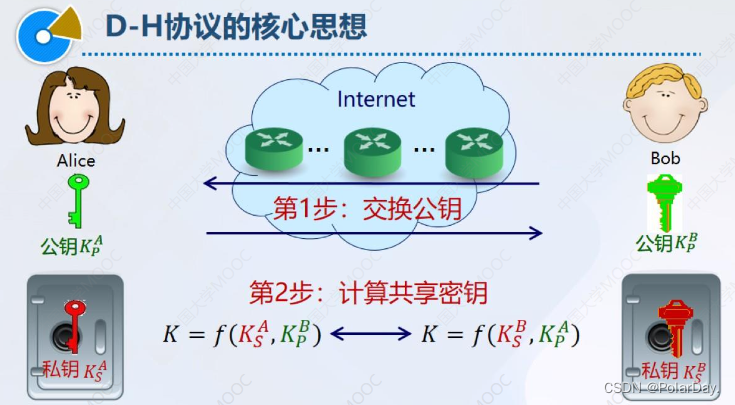
- Alice与Bob交换公钥
- 双方将收到的对方的公钥和自己的密钥通过函数f计算得到K
- 这样就实现了在事先不共享秘密信息的情况下得到了一个共享的密钥K,K经过进一步加工就可以作为对称密钥供双方使用。
(注意:这里的函数f必须是单向函数,否则由已知的函数结果K以及自己的公开密钥可以推出对方的私钥,这不是我们希望的结果)
用于构造双钥密码的单向函数:多项式求根、离散对数DL(Elgamal、DH)、大整数分解FAC(RSA、Rabin)、Diffie-Hellman问题(DHP) 公钥密码体制所基于的三大传统困难问题:有限域上的离散对数问题、大整数分解问题、椭圆曲线上的离散对数问题
理论基础单射
令函数f是集A到集B的映射,用f:A→B表示。若对于任意x1≠x2,x1,x2∈A,有f(x1)≠f(x2),则称f为单射,或1-1映射,或可逆的函数。
单向函数
一个可逆函数f:A→B,若它满足:
- 对所有x∈A,易于计算f(x);
- 对“几乎所有x∈A",由f(x)求x极为困难,以至于几乎是不可能的,则称f是一个单向函数。
陷门单向函数
陷门单向函数是一类满足下述条件的单向函数:
fz:Az→Bz,z∈Z,Z是陷门信息集合。
- 对所有z∈Z,在给定z下容易找到一对算法Ez和Dz,使对所有x∈A,易于计算fz及其逆,即: fz(x) = Ez(x); Dz(fz(x)) = x
- 对所有z∈Z,当只给定Ez和Dz时,对所有x∈A,很难从y = fz(x)计算出x。
区别:单向函数是求逆困难的函数,而陷门单向函数是在不知道陷门信息下求逆困难的函数。当知道陷门信息后,求逆易于实现。
公钥加密方案
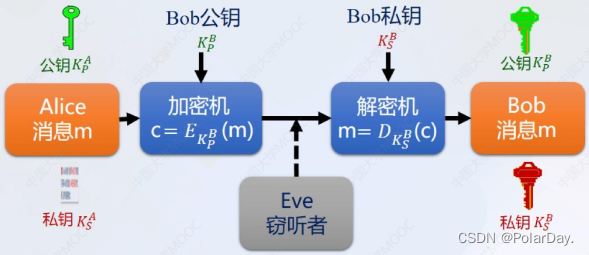
注意:公钥加密都是基于数学难题产生的,计算开销特别大,因此只有在迫不得已的情况下才使用公钥加密,对于大批量的报文还是采用对称加密算法
混合模式 使用公钥加密进行对称密钥的分发,使用对称加密进行应用数据的保密通信。
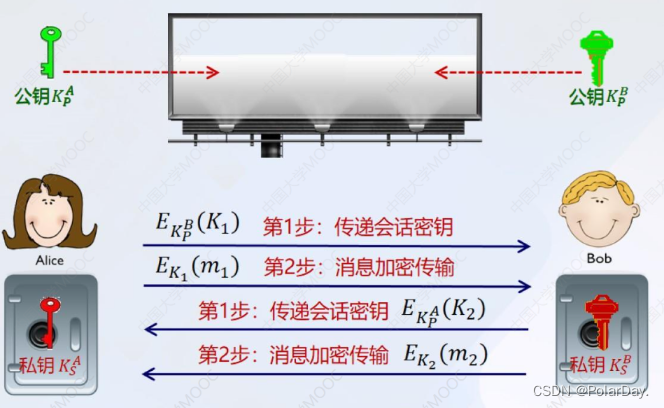
每个用户都拥有两个密钥:公钥和私钥
- 公钥(public-key): 可以被任何人知道,用于加密或验证签名。
- 私钥(private-key): 只能由持有者知道,用于解密或签名。
- 由私钥及其他密码信息容易计算出公开密钥;而由公钥及算法描述,计算私钥却非常困难。
公钥密钥体制解决了密钥的发布和管理问题
- 通信双方可以公开其公开密钥,而保留私钥。
- 发方可以用收方公钥对发送的信息进行加密。
- 收方用自己的私钥对收到的密文进行解密
密钥分发
- 用于交换秘密信息;
- 用于交换对称加密密钥。
消息加密
- 用于对消息直接加密;
- 用公钥加密,用私钥解密;
- 公钥算法能够用于密钥分配。
数字签名
- 发送方采用自己的私钥对消息进行签名;
- 接收方采用发送方的公钥对签名进行验证。
- 安全性依赖于解数学上的困难问题。
- 穷搜索(exhaustive search)在理论上能够破解公钥密码,当密钥足够长时,破解极其困难。
- 目前,通常要求足够大的密钥长度抵抗穷举攻击(>1024 bits)。
- 密钥太长会导致加密速度缓慢,因此公钥算法常用于密钥传递,而一般不用于实时的数据加密(实时数据加密使用对称密码算法)。
比如:https协议就是http协议加tls协议,tls协议是一个网络安全协议主要包括两个子协议——握手协议和记录协议,其中握手协议就在两个实体之间建立一个公共的密钥k,在记录协议阶段就可以凭借密钥k使用对称加密算法进行应用层数据的保密。
RSA密码体制RSA是一种分组密码,其理论基础是一种特殊的可逆模指数运算,其安全性基于大整数分解的困难性;既可用于消息加密,也可用于数字签名;硬件实现时比DES慢约1000倍,软件实现时比DES慢约100倍;目前多使用RSA公司的PKCS系列标准;RSA-155(密钥长度为512bit)于1999年被破解。
算法说明密钥生成算法(选、算、选、算)
- (选)选择两个不同的大素数p,q
- (算)计算n = p × q,及其欧拉函数值φ(n) = (p- 1)(q- 1)
- (选)随机选一整数e,1 ≤ e < φ(n),使得GCD(φ(n),e) = 1(即φ(n)与e互素)
- (算)计算模φ(n)下e的逆元: d = e-1 mod φ(n) (费马小定理、扩展欧几里得)
加解密算法
- 取公钥为n,e,私钥为d (p, q不再需要,可销毁,但绝不可泄露)。
- 加密变换为:m → c = me mod n
- 解密变换为:c → m = cd mod n
密钥选择
- 模数大于1024bit,p,q为大素数
- p - 1, q - 1有大的素因子
- p + 1, q + 1也要有大的素因子
- e不能太小,例如e值为3,17,65537,(216+1)(这些数字的二进制都只有两位1,在计算加密变换me可以通过快速幂加快计算速度;解密变换时解密方知道p和q,可以通过中国剩余定理加快计算速度)
- 注:这里的大素数选择,通常通过先产生伪随机数然后对产生的伪随机数判断是否是满足条件的素数,如果满足则采纳,如果不满足则再产生伪随机数进行判断。
使用
- 设Bob的公钥为(e , n),私钥为d,明文为m
- Alice用Bob的公钥做加密:c = me mod n,发给Bob
- Bob用Bob的私钥做解密:m = cd mod n
特点
- 即使A和B从来不认识,都可进行保密通信,只要A知道B的公钥。
- 速度慢,它不适用于对图像、话音等进行实时数据加密。
- 要求对公开密钥进行保护,防止攻击者对公钥的修改和替换。
- 选p1 = 47, p2 = 71,则n = 47 × 71 = 3337, φ(n) = 46 × 70 = 3220。 若选e = 79,可计算d = e -1(mod 3220) = 1019。
- 公开钥n = 3337和e = 79, 秘密钥d = 1019。销毁p1和p2。
- 令明文为x = 688 232 687 966 668 3,分组得x1=688,x2=232,x3=687, x4=966, x5=668, x6=3。
- 对x1加密为: (688)79 mod 3337 = 1570 = C1。
- 同样可计算出其它各组密文: y = 1570 2756 2714 2423 158
- 对C1解密: (1570)1019 mod 3337 = 668 = x1。类似地可解出其它各组密文,恢复出明文。
RSA算法的安全性主要基于模n分解的困难性,即给定两个大素数p和q,p * q = n,计算它们的乘积n是简单的,但是由n分解出p和q是困难的,注意这里的困难程度与n的大小有关,这里的n必须足够大
常见的攻击方法
- 低加密指数攻击
- 迭代攻击法
- 定时攻击法
- 选择密文攻击
- 消息隐匿问题
- 公用模攻击
- 其他途径
理论上,RSA的安全性取决于模n分解的困难性。
采用广义域筛所需计算机资源
密钥长(bit) 所需MIPS年 116 400 129 5000 512 30000 768 200 000 000 1024 300 000 000 000 2048 300 000 000 000 000现代计算机的性能远超于MIPS(每秒百万条指令)数量级,一般选择1024bit长的密钥才能保证安全
单钥和双钥密码在相同安全性下的等价密钥长度
单钥体制 RSA体制 56 b 384 b 64 b 512 b 80 b 768 b 112 b 1792 b 128 b 2304 b ElGamal密码体制EIGamal于1985年基于离散对数问题提出了一个既可用于数字签名又可用于加密的密码体制;(此方案的修改版被NIST采纳为美国的数字签名标准DSS)
算法说明密钥生成算法
- 选择素数p,设GF(p)上的本原元为g 通过计算 h = gα (mod p)可以求出有限域GF(p)中的任何一个元素 α∈[1,p-1],也就是说给定一个α一定可以计算得到一个有限域中的元素h;反过来给定一个有限域中的元素h,要求解α需要做对数运算,并且这里α取得是1到p-1中的离散值,因此称这种运算为离散对数运算。 当p足够大的时候还不存在一个多项式时间有效的解法求解α,因此称其为有限域上的离散对数困难问题。
- 选择密钥: α in GF(p)* (except 0)
- 计算公钥: β = gα mod p
加密算法
- 加密方选择一个随机数: k,且GCD(k,p - 1) = 1
- 加密: m → (gk,mβk) mod p = (y1,y2) = c
解密算法
- 解密: m = y2y1-α mod p
注意:加密方在每次加密时都会重新选择一个随机数k而不会重用之前的随机数,也就是说Elgamal每次加密相同信息时得到的结果是不同的
Elgamal在加密时会产生两个密文具有一个密文的扩张增加了通信的开销
有学者认为RSA是直线型的密码算法是一维的,Elgamal是平面型的密码算法是二维的,因为它需要发送方交互,即发送方也产生一部分密文信息(随机数k)来进行密码算法的完成,RSA算法则不需要发送方产生密文信息
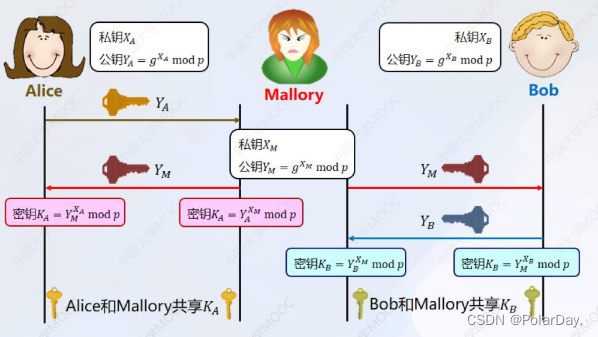
Diffie-Hellman公钥密码体制 密钥交换过程
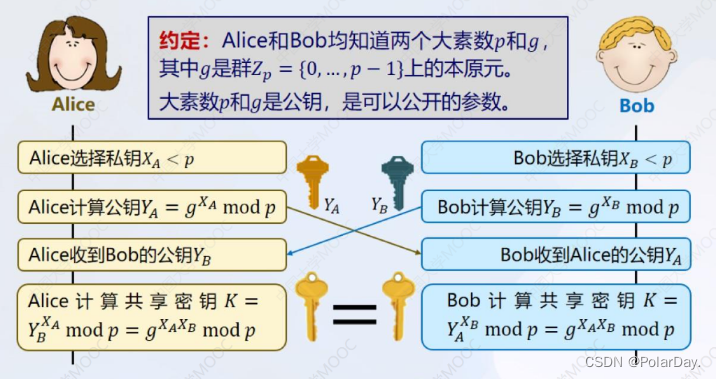

D-H协议可以抵抗被动攻击,但不能抵抗中间人攻击。 中间人攻击:通过拦截正常的网络通信数据,对通信内容进行嗅探和篡改,在这一过程中,正常通信的双方往往毫不知情。
椭圆曲线作为代数几何中的重要问题已有一百多年的研究历史。1985年,N. Koblitz和V. Miller才将其独立引入密码学中,使其成为构造公钥密码体制的一个有力工具。 我们知道有限域上的椭圆曲线点集可以构成群,在此群上定义离散对数系统,可以构造出基于有限域上离散对数问题的公钥密码体制。
优势椭圆曲线密码体制的安全性基于ECC离散对数问题,目前尚未发现明显的弱点。在公钥密码的标准化过程中,IEEE P1363标准已经采用了ECC。 相比于RSA密码体制,椭圆曲线密码体制最大的优势在于可以使用比 RSA 更短的密钥来获得相同水平的安全性,从而使计算量大大减少。
ECC的密钥长度 RSA的密钥长度 MIPS年 ECC:RSA密钥长度比 106 512 104 1:5 132 768 108 1:6 160 1024 1011 1:7 210 2048 1020 1:10 600 21000 1078 1:35因此,椭圆曲线适合于存储空间受限、通信能力受限的环境中:
- 无线MODEM: ECC可以实现快速Diffie- Hellman密钥交换,占用带宽达到最小化,计算时间从60s降到20s。
- Web服务器: ECC可以节省计算的时间和带宽,并且通过算法的协商更易于处理兼容性问题。
- 集成电路卡: ECC无需协处理器就可以在IC卡上实现快速安全的数字签名,大大降低了IC卡的成本。
实数域上的椭圆曲线可以定义为满足方程:y2 = x3 + ax + b的所有点(x, y)的集合。 注意:椭圆曲线并不是椭圆,只因为该方程与计算椭圆周长的方程相似。
可以证明:如果x3 + ax + b没有重复因子,或者满足4a3 + 27b2≠0,那么椭圆曲线上的点集E(a, b)可构成一个Abel群。
椭圆曲线群包括所有曲线上的点以及一个特殊的点,我们称其为无限远点O。
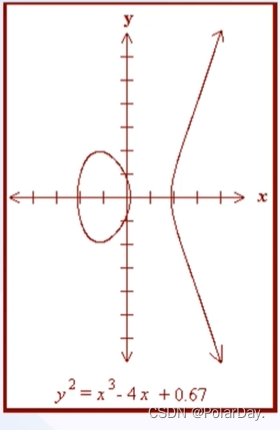
椭圆曲线实例
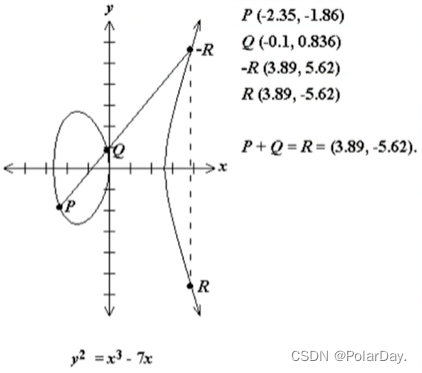
一、P + Q = R
P,Q都取一般点的计算,连接P,Q作延长线与曲线交于点-R,取交点-R与x轴的对称点R即可得到P+Q的值
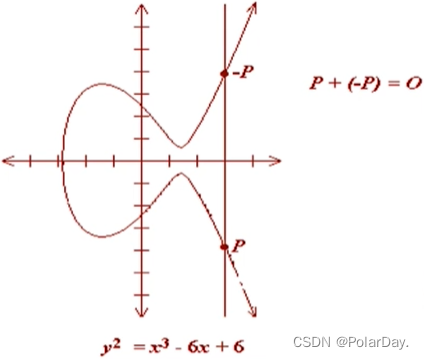
二、P + (-P) = O
当Q取-P即P,Q连线与x轴垂直时,P + (-P)的结果是无穷远点
 三、2P = P + P = R
当Q等于P时,做P点的切线,与曲线交于点-R,取-R关于x轴的对称点就是2P的结果R
三、2P = P + P = R
当Q等于P时,做P点的切线,与曲线交于点-R,取-R关于x轴的对称点就是2P的结果R
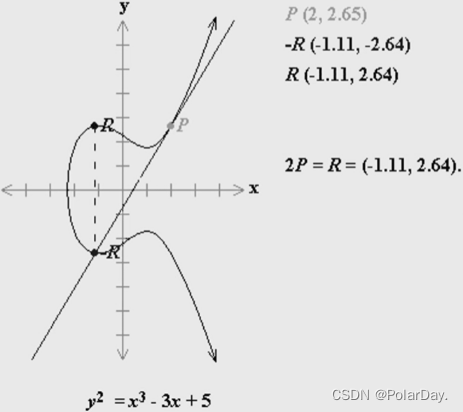
有限域GF(p)上的椭圆曲线 y2 = x3 + ax+ b,其点集(x, y)构成有限域上的Abel群,记为Ep(a, b)。条件为: 4a3 + 27b2 ≠ 0 mod p
设P = (x1,y1),Q = (x2,y2), P + Q = (x3, y3) 计算公式与之前实数域上的相同,只需要再加一个模p
-
当P ≠ Q时: λ = ( y 2 − y 1 x 2 − x 1 \frac{y_2-y_1}{x_2-x_1} x2−x1y2−y1) mod p x3 = (λ2 - x1 - x2) mod p y3 = (λ(x1 - x3) - y1) mod p
-
当P = Q时: λ = ( 3 x 1 2 + a 2 y 1 \frac{3x_1^2 + a}{2y_1} 2y13x12+a) mod p x3 = (λ2 - x1 - x2) mod p y3 = (λ(x1 - x3) - y1) mod p
- 取p = 23, a = b = 1,则椭圆曲线方程为: y2 = x3 + x + 1 mod p
- 把满足上式的所有点(x, y)和元素O所组成的点集记为E23(1,1)。
- 对于E23(1, 1),只关心满足模p方程的、从(0, 0)到(p-1,p-1)的象限中的非负整数。下表列出E23(1,1)若干点(O点除外)。
y2 mod p = (x3 + ax + b) mod p (1) 系数满足: 4a3 + 27b2 ≠ 0 mod p (2) 说明:对于有限域GF(p)上的椭圆曲线,使用变元和系数均在0到p-1的整数集上取值的三次方程,其中p是大素数,所执行的运算均为模p运算。
例如: a=1,b=1,p=23, 椭圆曲线E23(1,1)系数可满足(2)式: 4 × 13 + 27 × 12 = 31 mod 23 ≠ 0 且x=9,y=7时,(1)式的两边分别为: 72 mod 23 = (93 + 9 + 1) mod 23 49 mod 23 = 739 mod 23 3 mod 23 = 3 mod 23 相等,所以(9,7)在曲线上
将表格中的点在图像上表示出来,可以看到曲线上的点都是离散分布的
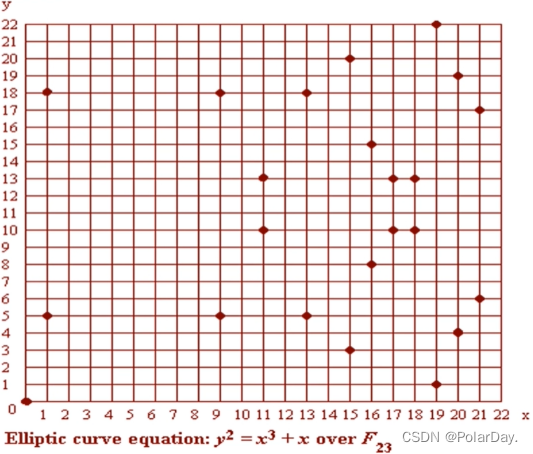
例如: E23(1,1)为一椭圆曲线,设P=(3,10), Q=(9,7),则: λ = ( y 2 − y 1 x 2 − x 1 \frac{y_2-y_1}{x_2-x_1} x2−x1y2−y1) mod p x3 = (λ2 - x1 - x2) mod p y3 = (λ(x1 - x3) - y1) mod p
可以求出: λ = ( 7 − 10 9 − 3 \frac{7-10}{9-3} 9−37−10) mod 23 = ( − 1 2 \frac{-1}{2} 2−1) mod 23 = 11 x3 = (112 - 3 - 9) mod 23 = 109 mod 23 = 17 y3 = (11 × (3 - 17) - 10) mod 23 = -164 mod 23 = 20
所以: P+Q=(17,20) 可以看出P+Q仍然为椭圆曲线E23(1,1)上的点
设P=(3,10),则2P的计算为: λ = ( 3 x 1 2 + a 2 y 1 \frac{3x_1^2 + a}{2y_1} 2y13x12+a) mod p x3 = (λ2 - x1 - x2) mod p y3 = (λ(x1 - x3) - y1) mod p
可以求出: x3 = 7,y3 = 12 所以:2P=(7,12) 可以看出: 2P仍然为椭圆曲线E23(1,1)上的点。 同理,我们可以求出: 4P=P+P+P+P
有限域Ep(a,b)上的椭圆曲线结论- 从上例可以看出:加法运算在E23(1,1)上是封闭的,且还能验证满足交换律。
- 对于一般形式的Ep(a,b),可证明其上的加法运算是封闭的,且满足交换律。
- 同样,我们还可以证明Ep(a,b)上的加法逆元运算也是封闭的。
- 根据群的定义可知,Ep(a,b)是一一个Abel群。
- 关于X轴对称
- 画一条直线跟椭圆曲线相交,它们最多有三个交点
- 1P= P 2P=P+P 3P=2P+P … k*P=(k-1)*P+P 举例:因为23=16+4+2+1,所以23P=16P+4P + 2P + P总共只需要7次加法(P+P、2P+2P、4P+4P、8P+8P、P+2P、3P+4P、7P+16P)。
为了使用椭圆曲线构造公钥密码体制,需要找出椭圆曲线上的数学难题。
椭圆曲线上的离散对数问题——ECDLP
在椭圆曲线构成的Abel群Ep(a,b)上,考虑方程: Q=kP, 其中P,Q∈Ep(a,b),k
最近更新
- 深拷贝和浅拷贝的区别(重点)
- 【Vue】走进Vue框架世界
- 【云服务器】项目部署—搭建网站—vue电商后台管理系统
- 【React介绍】 一文带你深入React
- 【React】React组件实例的三大属性之state,props,refs(你学废了吗)
- 【脚手架VueCLI】从零开始,创建一个VUE项目
- 【React】深入理解React组件生命周期----图文详解(含代码)
- 【React】DOM的Diffing算法是什么?以及DOM中key的作用----经典面试题
- 【React】1_使用React脚手架创建项目步骤--------详解(含项目结构说明)
- 【React】2_如何使用react脚手架写一个简单的页面?



