密码学算法——RSA

RSA算法

RSA第一次在R.L. Rivest，A. Shamir和L. Adleman的1978年的论文《A method for obtaining digital signatures and public key cryptosystems》中，作为一种新的数字签名和公钥密码学算法提出，RSA分别取三位作者姓氏首字母组成。

形象解释可参看：如何深入浅出地讲解RSA密码？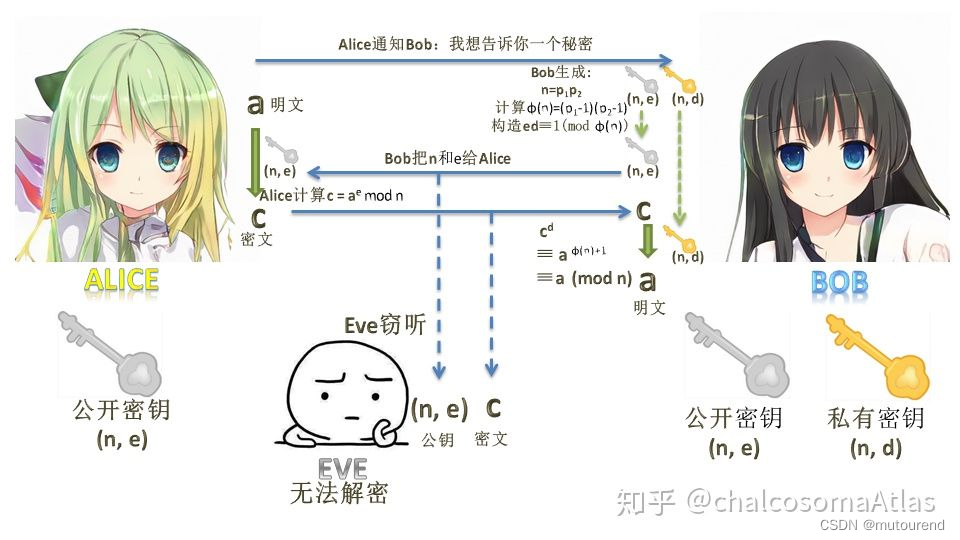

RSA算法由来

RSA算法是非对称加密算法中的重要组成成员之一，其主要安全壁垒在于两个大素数乘积的因式分解难度。

RSA算法关键细节 RSA公私钥计算细节

RSA算法的关键流程为： 1）p,q：任意的两个素数（保密，不对外泄露） 2）n：=pq（对外已知，与e一起组成公钥） 3）d：1~n-1之间的随机数（仅对密钥所有者已知，实际即为私钥） 4）e：满足de≡1(mod (p-1)*(q-1)) （对外已知，与n一起组成公钥） RSA非对称加密算法中的公钥为(e,n)，私钥为d。其中的素数p和q应对任何人均不可知。

RSA加密细节

通过公钥(e,n)对消息m（m值的范围为0~n-1）进行加密， 加密后的消息c（c值的范围为0~n-1）为： c=E(m):=(me)%n

RSA解密细节

通过私钥对密文c进行解密： D( c):=(cd)%n 具体解密实现的数学依据为： ∵ cd ≡ (me%n)d ≡ med(mod n) ∵ de ≡ 1(mod (p-1)(q-1)) ∴ med(mod n) ≡ m(mod n) ∵ c值的范围为0~n-1 ∵ m值的范围为0~n-1 ∴ D( c) = m 通过私钥d对密文c进行解密可成功获取相应的明文m。

RSA算法安全瓶颈

RSA算法的安全性依赖于n的因式分解难度，使得根据公钥e无法计算破解得到私钥d，若n易于因式分解，则可知p和q，由e获取私钥d则很容易，整个RSA算法的安全性将无法保证。

RSA算法的乘法同态特性

RSA加密算法具有的乘法同态特性，依赖于其E加密算法数学特征： E(x)E(y) ≡ xeye ≡ (xy)e ≡ E(xy) 这种同态特性可在零知识证明中发挥作用，即无需暴露x和y的具体值，prover证明者仅通过发送加密的信息a=E(x)、b=E(y)和c=E(xy)，verifier验证者仅需验证确认(a*b)%n ≡ c%n成立，即可说明prover发送的是两个数值及其相应乘积。

参考资料： [1] 1978年论文《A Method for Obtaining Digital Signatures and Public-Key Cryptosystems》