Montgomery curve为椭圆曲线的一种，基于Fq的仿射方程表示为： E ( A ; B ) : B y 2 = x ( x 2 + A x + 1 ) E(A;B) : By^2 = x(x^2 + Ax + 1) E(A;B):By2=x(x2+Ax+1) 其中参数A和B为在域Fq内的值，同时满足 B != 0, A2 != 4。
将上述方程转换为投影坐标系下(X : Y : Z)，其中x = X/Z, y = Y/Z，则对应的投影模型： E ( A ; B ) : B Y 2 Z = X ( X 2 + A X Z + Z 2 ) ⊆ P 2 E(A;B) : BY^2Z = X(X^2 + AXZ + Z^2) \subseteq P^2 E(A;B):BY2Z=X(X2+AXZ+Z2)⊆P2
对于投影模型的表示下，E(A;B) 上有一个无穷远点 O = (0 : 1 : 0)，该点位E(A;B) 上唯一的一个Z=0点。
2. P1上的快速微分运算在投影坐标系下，quotient map(商映射关系) F : E ( A ; B ) ↦ E / < ⊖ > = P 1 F:E(A;B) \mapsto E/<\ominus >=P^1 F:E(A;B)↦E/=P1 为： F : P ↦ { ( x p : 1 ) i f P = ( x p : y p : 1 ) ( 1 : 0 ) i f P = O = ( 0 : 1 : 0 ) F:P\mapsto\left\{\begin{matrix} (x_p:1) & if &P=(x_p:y_p:1) \\ (1:0)& if &P=O=(0:1:0) \end{matrix}\right. F:P↦{(xp:1)(1:0)ififP=(xp:yp:1)P=O=(0:1:0)
即 F ( ( X : Y : Z ) ) = ( X : Z ) F((X:Y:Z))=(X:Z) F((X:Y:Z))=(X:Z)仅对Z!=0的情况成立。对于无穷远点O=(0:1:0)，(0:0)不是投影坐标点。 T=(0:0:1)。
2.1 P1上的伪运算{ F ( P ) , F ( Q ) , F ( P ⊕ Q ) , F ( P ⊖ Q ) } \begin{Bmatrix} F(P),F(Q),F(P\oplus Q),F(P\ominus Q) \end{Bmatrix} {F(P),F(Q),F(P⊕Q),F(P⊖Q)} 上面集合中知道任意三个值，即可计算出第四个值。
- 伪加法运算—— F A D D : ( F ( P ) , F ( Q ) , F ( P ⊖ Q ) ) ↦ F ( P ⊕ Q ) F_{ADD}:(F(P),F(Q),F(P\ominus Q)) \mapsto F(P\oplus Q) FADD:(F(P),F(Q),F(P⊖Q))↦F(P⊕Q)
- 当P=Q时，即为伪double运算—— F D B L : F ( P ) ↦ F ( [ 2 ] P ) F_{DBL}:F(P) \mapsto F([2]P) FDBL:F(P)↦F([2]P)
以上的伪加法和伪double运算为高效伪乘法运算的基础。
假设 P = ( x p , y p ) , Q = ( x q , y q ) , 且 x p ! = 0 , x q ! = 0 P=(x_p,y_p), Q=(x_q,y_q), 且x_p!=0, x_q!=0 P=(xp,yp),Q=(xq,yq),且xp!=0,xq!=0：
-
当P!=Q时，Montgomery发现 P , Q , P ⊕ Q , P ⊖ Q P, Q, P\oplus Q,P\ominus Q P,Q,P⊕Q,P⊖Q这四个点的x坐标值存在如下关系： x P ⊕ Q x P ⊖ Q ( x P − x Q ) 2 = ( x P x Q − 1 ) 2 x_{P\oplus Q}x_{P\ominus Q}(x_P-x_Q)^2=(x_Px_Q-1)^2 xP⊕QxP⊖Q(xP−xQ)2=(xPxQ−1)2
-
当P=Q时，将[2]P表示为 [ 2 ] P = ( x [ 2 ] P , y [ 2 ] P ) [2]P=(x_{[2]P},y_{[2]P}) [2]P=(x[2]P,y[2]P)，则有 4 x [ 2 ] P x P ( x P 2 + A x P + 1 ) = ( x P 2 − 1 ) 2 4x_{[2]P}x_P(x_P^2+Ax_P+1)=(x_P^2-1)^2 4x[2]PxP(xP2+AxP+1)=(xP2−1)2
以上两个公式对于Weierstrass模型也成立，只是不如Montgomery curve直观。
具体计算细节参见论文《Speeding the Pollard and Elliptic Curve Methods of Factorization》： 
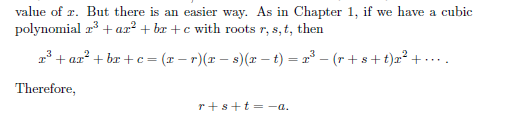
实际运算时，更多关注已知 F ( P ) , F ( Q ) , F ( P ⊖ Q ) F(P),F(Q),F(P\ominus Q) F(P),F(Q),F(P⊖Q)求解 F ( P ⊕ Q ) F(P\oplus Q) F(P⊕Q)，即对伪加法运算的获取。 假设P!=Q且 P ⊖ Q ! = T P\ominus Q != T P⊖Q!=T，根据第2节公式定义有： ( X P : Z P ) : = F ( P ) , ( X Q : Z Q ) : = F ( Q ) , ( X ⊕ : Z ⊕ ) : = F ( P ⊕ Q ) , ( X ⊖ : Z ⊖ ) : = F ( P ⊖ Q ) (X_P:Z_P):=F(P) ,\quad (X_Q:Z_Q):=F(Q), \quad (X_{\oplus}:Z_{\oplus}):=F(P\oplus Q), \quad (X_{\ominus}:Z_{\ominus}):=F(P\ominus Q) (XP:ZP):=F(P),(XQ:ZQ):=F(Q),(X⊕:Z⊕):=F(P⊕Q),(X⊖:Z⊖):=F(P⊖Q)
根据假设，可知 P ⊖ Q ∉ { O , T } P\ominus Q \notin \{O,T\} P⊖Q∈/{O,T}，所以 X ⊖ ! = 0 , Z ⊖ ! = 0 X_{\ominus} != 0, Z_{\ominus} != 0 X⊖!=0,Z⊖!=0， 在投影坐标系下(X:Y:Z)下计算，因为 x = X / Z , y = Y / Z , E ( A ; B ) : B Y 2 Z = X ( X 2 + A X Z + Z 2 ) ⊆ P 2 x = X/Z, y = Y/Z, E(A;B) : BY^2Z = X(X^2 + AXZ + Z^2) \subseteq P^2 x=X/Z,y=Y/Z,E(A;B):BY2Z=X(X2+AXZ+Z2)⊆P2,对于： x P ⊕ Q x P ⊖ Q ( x P − x Q ) 2 = ( x P x Q − 1 ) 2 x_{P\oplus Q}x_{P\ominus Q}(x_P-x_Q)^2=(x_Px_Q-1)^2 xP⊕QxP⊖Q(xP−xQ)2=(xPxQ−1)2 可转换为： X ⊕ Z ⊕ X ⊖ Z ⊖ ( X P Z P − X Q Z Q ) 2 = ( X P Z P X Q Z Q − 1 ) 2 \frac{X_{\oplus}}{Z_{\oplus}}\frac{X_{\ominus}}{Z_{\ominus}}(\frac{X_P}{Z_P}-\frac{X_Q}{Z_Q})^2=(\frac{X_P}{Z_P}\frac{X_Q}{Z_Q}-1)^2 Z⊕X⊕Z⊖X⊖(ZPXP−ZQXQ)2=(ZPXPZQXQ−1)2 约简为： X ⊕ Z ⊕ = Z ⊖ X ⊖ ( X P Z P − X Q Z Q ) 2 ( X P Z Q − X Q Z P ) 2 = Z ⊖ [ ( X P − Z P ) ( X Q + Z Q ) + ( X P + Z P ) ( X Q − Z Q ) ] 2 X ⊖ [ ( X P − Z P ) ( X Q + Z Q ) − ( X P + Z P ) ( X Q − Z Q ) ] 2 \frac{X_{\oplus}}{Z_{\oplus}} = \frac{Z_{\ominus}}{X_{\ominus}}\frac{({X_P}{Z_P}-{X_Q}{Z_Q})^2}{({X_P}{Z_Q}-{X_Q}{Z_P})^2}=\frac{Z_{\ominus}[(X_P-Z_P)(X_Q+Z_Q)+(X_P+Z_P)(X_Q-Z_Q)]^2}{X_{\ominus}[(X_P-Z_P)(X_Q+Z_Q)-(X_P+Z_P)(X_Q-Z_Q)]^2} Z⊕X⊕=X⊖Z⊖(XPZQ−XQZP)2(XPZP−XQZQ)2=X⊖[(XP−ZP)(XQ+ZQ)−(XP+ZP)(XQ−ZQ)]2Z⊖[(XP−ZP)(XQ+ZQ)+(XP+ZP)(XQ−ZQ)]2 相应地，可计算 ( X ⊕ , Z ⊕ ) (X_{\oplus}, Z_{\oplus}) (X⊕,Z⊕)： { X ⊕ = Z ⊖ [ ( X P − Z P ) ( X Q + Z Q ) + ( X P + Z P ) ( X Q − Z Q ) ] 2 Z ⊕ = X ⊖ [ ( X P − Z P ) ( X Q + Z Q ) − ( X P + Z P ) ( X Q − Z Q ) ] 2 \left\{\begin{matrix} X_{\oplus}=Z_{\ominus}[(X_P-Z_P)(X_Q+Z_Q)+(X_P+Z_P)(X_Q-Z_Q)]^2\\ Z_{\oplus}=X_{\ominus}[(X_P-Z_P)(X_Q+Z_Q)-(X_P+Z_P)(X_Q-Z_Q)]^2 \end{matrix}\right. {X⊕=Z⊖[(XP−ZP)(XQ+ZQ)+(XP+ZP)(XQ−ZQ)]2Z⊕=X⊖[(XP−ZP)(XQ+ZQ)−(XP+ZP)(XQ−ZQ)]2
若 F ( P ⊖ Q ) F(P\ominus Q) F(P⊖Q)的“difference”为固定的，则可归一化为 ( X P : 1 ) (X_P:1) (XP:1)。
伪加法运算中，与曲线参数A，B均无关。
具体的算法实现可如下： 
可参见2.2节中类似的公式转换，可计算 ( X [ 2 ] P , Z [ 2 ] P ) (X_{[2]P},Z_{[2]P}) (X[2]P,Z[2]P)： { X [ 2 ] P = ( X P + Z P ) 2 ( X P − Z P ) 2 Z [ 2 ] P = ( 4 X P Z P ) [ ( X P − Z P ) 2 + ( A + 2 ) 4 ( 4 X P Z P ) ] \left\{\begin{matrix} X_{[2]P}=(X_P+Z_P)^2(X_P-Z_P)^2\\ Z_{[2]P}=(4X_PZ_P)[(X_P-Z_P)^2+\frac{(A+2)}{4}(4X_PZ_P)] \end{matrix}\right. {X[2]P=(XP+ZP)2(XP−ZP)2Z[2]P=(4XPZP)[(XP−ZP)2+4(A+2)(4XPZP)] 其中： 4 X p Z P = ( X P + Z P ) 2 − ( X P − Z P ) 2 4X_pZ_P=(X_P+Z_P)^2-(X_P-Z_P)^2 4XpZP=(XP+ZP)2−(XP−ZP)2
伪double运算中，X的值与曲线参数A,B均无关；Z的值仅使用了曲线的参数A，与曲线参数B无关。
相应的算法实现如下： 
上面算法的步骤7中，做的是一个与常量
(
A
+
2
)
/
4
(A+2)/4
(A+2)/4的乘积运算。因此实际A参数越小，越能减少该常量乘积运算的开销。
参考资料： [1] 论文《Speeding the Pollard and Elliptic Curve Methods of Factorization》 [2] 论文《Montgomery curves and their arithmetic》
