edwards25519 curve表示为：
− x 2 + y 2 = 1 + d x 2 y 2 , d = − ( 121665 / 121666 ) , q = 2 255 − 19 -x^2+y^2=1+dx^2y^2,d=-(121665/121666),q=2^{255}-19 −x2+y2=1+dx2y2,d=−(121665/121666),q=2255−19
根据博客Extended twisted Edwards curve坐标系中提及：
注意，在Extended坐标系下，可提供更快的加法运算，在Projective坐标系下，可提供更快的double运算！！！实际使用时，可根据不同的计算选择不同的坐标系。
所以，double运算采用论文《Twisted Edwards Curves》中的Doubling in Projective Twisted Coordinates算法：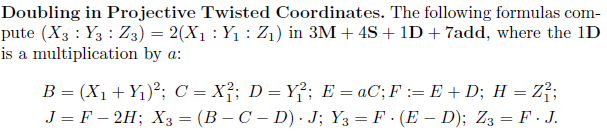 
对于edwards25519 curve，
a
=
−
1
a=-1
a=−1。同时根据https://doc-internal.dalek.rs/curve25519_dalek/backend/serial/curve_models/index.html 中定义，对应的Projective坐标为
(
W
1
:
W
2
:
W
3
)
(W_1:W_2:W_3)
(W1:W2:W3)，详细的计算过程为：
B
=
(
X
1
+
Y
1
)
2
;
C
=
X
1
2
;
D
=
Y
1
2
;
E
=
a
C
=
−
X
1
2
;
F
:
=
E
+
D
=
Y
1
2
−
X
1
2
;
H
=
Z
1
2
;
J
=
F
−
2
H
=
Y
1
2
−
X
1
2
−
2
Z
1
2
B=(X_1+Y_1)^2; C=X_1^2;D=Y_1^2;E=aC=-X_1^2;F:=E+D=Y_1^2-X_1^2; H=Z_1^2;J=F-2H=Y_1^2-X_1^2-2Z_1^2
B=(X1+Y1)2;C=X12;D=Y12;E=aC=−X12;F:=E+D=Y12−X12;H=Z12;J=F−2H=Y12−X12−2Z12
⇒
W
1
=
X
3
=
(
B
−
C
−
D
)
∗
J
=
[
(
X
1
+
Y
1
)
2
−
(
X
1
2
+
Y
1
2
)
]
∗
(
Y
1
2
−
X
1
2
−
2
Z
1
2
)
\Rightarrow W_1=X_3=(B-C-D)*J=[(X_1+Y_1)^2-(X_1^2+Y_1^2)]*(Y_1^2-X_1^2-2Z_1^2)
⇒W1=X3=(B−C−D)∗J=[(X1+Y1)2−(X12+Y12)]∗(Y12−X12−2Z12)
⇒
W
2
=
Y
3
=
F
∗
(
E
−
D
)
=
(
Y
1
2
−
X
1
2
)
∗
(
−
X
1
2
−
Y
1
2
)
\Rightarrow W_2=Y_3=F*(E-D)=(Y_1^2-X_1^2)*(-X_1^2-Y_1^2)
⇒W2=Y3=F∗(E−D)=(Y12−X12)∗(−X12−Y12)
⇒
W
3
=
Z
3
=
F
∗
J
=
(
Y
1
2
−
X
1
2
)
∗
(
Y
1
2
−
X
1
2
−
2
Z
1
2
)
\Rightarrow W_3=Z_3=F*J=(Y_1^2-X_1^2)*(Y_1^2-X_1^2-2Z_1^2)
⇒W3=Z3=F∗J=(Y12−X12)∗(Y12−X12−2Z12)
∵ W 1 W 3 = X T Z T = X Z = x = ( X 1 + Y 1 ) 2 − ( X 1 2 + Y 1 2 ) Y 1 2 − X 1 2 \because \frac{W_1}{W_3}=\frac{XT}{ZT}=\frac{X}{Z}=x=\frac{(X_1+Y_1)^2-(X_1^2+Y_1^2)}{Y_1^2-X_1^2} ∵W3W1=ZTXT=ZX=x=Y12−X12(X1+Y1)2−(X12+Y12) ∵ W 2 W 3 = Y Z Z T = Y T = y = X 1 2 + Y 1 2 2 Z 1 2 − ( Y 1 2 − X 1 2 ) \because \frac{W_2}{W_3}=\frac{YZ}{ZT}=\frac{Y}{T}=y=\frac{X_1^2+Y_1^2}{2Z_1^2-(Y_1^2-X_1^2)} ∵W3W2=ZTYZ=TY=y=2Z12−(Y12−X12)X12+Y12 ∴ X = ( X 1 + Y 1 ) 2 − ( X 1 2 + Y 1 2 ) ; Y = X 1 2 + Y 1 2 ; Z = Y 1 2 − X 1 2 ; T = 2 Z 1 2 − ( Y 1 2 − X 1 2 ) \therefore X=(X_1+Y_1)^2-(X_1^2+Y_1^2); Y=X_1^2+Y_1^2; Z=Y_1^2-X_1^2; T=2Z_1^2-(Y_1^2-X_1^2) ∴X=(X1+Y1)2−(X12+Y12);Y=X12+Y12;Z=Y12−X12;T=2Z12−(Y12−X12)
以上得到的即为 σ : ( ( X : Z ) , ( Y : T ) ) \sigma :((X:Z),(Y:T)) σ:((X:Z),(Y:T))。相应的代码实现为：
// ------------------------------------------------------------------------
// Doubling
// ------------------------------------------------------------------------
impl ProjectivePoint {
/// Double this point: return self + self
pub fn double(&self) -> CompletedPoint { // Double()
let XX = self.X.square();
let YY = self.Y.square();
let ZZ2 = self.Z.square2();
let X_plus_Y = &self.X + &self.Y;
let X_plus_Y_sq = X_plus_Y.square();
let YY_plus_XX = &YY + &XX;
let YY_minus_XX = &YY - &XX;
CompletedPoint{
X: &X_plus_Y_sq - &YY_plus_XX,
Y: YY_plus_XX,
Z: YY_minus_XX,
T: &ZZ2 - &YY_minus_XX
}
}
}
由于有： σ : ( ( X : Z ) , ( Y : T ) ) ↦ ( X Y : X T : Z Y : Z T ) ↦ ( T ′ : X ′ : Y ′ : Z ′ ) \sigma :((X:Z),(Y:T))\mapsto(XY:XT:ZY:ZT)\mapsto(T':X':Y':Z') σ:((X:Z),(Y:T))↦(XY:XT:ZY:ZT)↦(T′:X′:Y′:Z′) 对应的 ( X ′ : Y ′ : Z ′ : T ′ ) (X':Y':Z':T') (X′:Y′:Z′:T′)即为extended坐标系表示，有： X ′ = X T ; Y ′ = Z Y ; Z ′ = Z T ; T ′ = X Y X'=XT; Y'=ZY; Z'=ZT; T'=XY X′=XT;Y′=ZY;Z′=ZT;T′=XY
对应的代码实现为：
/// Convert this point from the \\( \mathbb P\^1 \times \mathbb P\^1
/// \\) model to the \\( \mathbb P\^3 \\) model.
///
/// This costs \\(4 \mathrm M \\).
pub fn to_extended(&self) -> EdwardsPoint {
EdwardsPoint {
X: &self.X * &self.T,
Y: &self.Y * &self.Z,
Z: &self.Z * &self.T,
T: &self.X * &self.Y,
}
}
参考资料： [1] Extended twisted Edwards curve坐标系 [2] 论文《Twisted Edwards Curves》 [3] https://doc-internal.dalek.rs/curve25519_dalek/backend/serial/curve_models/index.html
