Extended twisted Edwards curve坐标系及相互转换中指出了,Every Edwards curve has a point of order 4. 论文《Decaf-Eliminating cofactors through point compression 2015-673》中对cofactor=4的曲线进行了压缩,保证了所使用的point步骤small-cofactor subgroup中。若使用small-cofactor subgroup中的point,存在的small-subgroup attack等危害参见博客ristretto对cofactor>1的椭圆曲线(如Curve25519等)的兼容(含Curve25519 cofactor的sage验证)。
以下为对cofactor=4的Edwards(或twisted Edwards curve ε \varepsilon ε)曲线进行压缩和解压缩算法梳理: 该曲线的order为 r = h q , h = 4 r=hq,h=4 r=hq,h=4,其中 q q q为素数。为了消除cofactor subgroup,实际要选择的group为 ε / ε [ 4 ] \varepsilon/\varepsilon[4] ε/ε[4]。(group群的一些基本概念可参见博客Elliptic curve isogeny and group coset) 同时,对于曲线 ε \varepsilon ε上的点,若两个点有small order(可被4整除),则认为该两点等价。需要涉及以下三方面的调整:
- 判断points等价的方法需调整,差异为4 order的点应视为等价。
- 在发送前必须压缩point,同时保证对等价的points,压缩后的序列表示 { 0 , 1 } n \{0,1\}^n {0,1}n也应相同。压缩后的结果为一个Field域内的非负数元素(具体定义见Non-negative field elements)。
- 解压缩时,应保证仅对有效point的压缩结果进行解压缩。
Non-negative field elements定义: 若 x ∈ F p , 且 x ∈ [ 0 , ( p − 1 ) / 2 ] x\in F_p,且x\in [0,(p-1)/2] x∈Fp,且x∈[0,(p−1)/2],则 x x x可称为field域内的非负数。否则,称为field域内的负数。
在论文《Decaf-Eliminating cofactors through point compression 2015-673》中提到,对于曲线表现形式选择为Montgomery curve的原因为:Montgomery curves give simple Diffie-Hellman protocols, and twisted Edwards curves give a speed boost but have incomplete formulas in fields of order 3 (mod 4).
1.1 Twisted Edwards curves表示Twisted Edwards curves的affine坐标系表示为: ε a , d : = { ( x , y ) ∈ P 2 ( F ) : a ∗ x 2 + y 2 = 1 + d ∗ x 2 ∗ y 2 } \varepsilon_{a,d}:=\{(x,y)\in P^2(F):a*x^2+y^2=1+d*x^2*y^2\} εa,d:={(x,y)∈P2(F):a∗x2+y2=1+d∗x2∗y2}
对应的Extended坐标系表示为: ε a , d : = { ( X : Y : Z : T ) ∈ P 3 ( F ) : X Y = Z T a n d a ∗ X 2 + Y 2 = Z 2 + d ∗ T 2 } \varepsilon_{a,d}:=\{(X:Y:Z:T)\in P^3(F):XY=ZT\ and\ a*X^2+Y^2=Z^2+d*T^2\} εa,d:={(X:Y:Z:T)∈P3(F):XY=ZT and a∗X2+Y2=Z2+d∗T2}
Edwards curve的identity point表示为 ( 0 , 1 ) = ( 0 : 1 : 1 : 0 ) (0,1)=(0:1:1:0) (0,1)=(0:1:1:0)。
通常地,当 a = 1 a=1 a=1时,为untwisted;当 a = − 1 a=-1 a=−1时,具有更高的计算速度。
由于edwards25519满足完备性条件,所以,其4-torsion subgroup is cyclic: ε a , d [ 4 ] = { ( 0 , 1 ) , ( 1 / a , 0 ) , ( 0 , − 1 ) , ( − 1 / a , 0 ) } \varepsilon_{a,d}[4]=\{(0,1),(1/\sqrt a,0),(0,-1), (-1/\sqrt a, 0)\} εa,d[4]={(0,1),(1/a ,0),(0,−1),(−1/a ,0)} 这些4-torsion points为edwards25519上仅有的满足 x y = 0 xy=0 xy=0的点。且其中的 y ! = 0 y!=0 y!=0点(即 ( 0 , 1 ) , ( 0 , − 1 ) (0,1),(0,-1) (0,1),(0,−1))为2-torsion point。可定义Group H = { ( 0 , 1 ) , ( 1 / a , 0 ) , ( 0 , − 1 ) , ( − 1 / a , 0 ) } H=\{(0,1),(1/\sqrt a,0),(0,-1), (-1/\sqrt a, 0)\} H={(0,1),(1/a ,0),(0,−1),(−1/a ,0)}
若a在有限域内存在平方根, a ∗ x 2 + y 2 = 1 + d ∗ x 2 ∗ y 2 a*x^2+y^2=1+d*x^2*y^2 a∗x2+y2=1+d∗x2∗y2可变形为: a ∗ ( y a ) 2 + ( a x ) 2 = 1 + d ∗ ( y a ) 2 ∗ ( a x ) 2 a*(\frac{y}{\sqrt a})^2+(\sqrt ax)^2=1+d*(\frac{y}{\sqrt a})^2*(\sqrt ax)^2 a∗(a y)2+(a x)2=1+d∗(a y)2∗(a x)2 ε a , d \varepsilon_{a,d} εa,d上的point点除可表示为 ( x , y ) , ( − x , − y ) (x,y),(-x,-y) (x,y),(−x,−y)外,亦可表示为 ( y / a , − a x ) , ( y / a , − a x ) (y/\sqrt a,-\sqrt ax),(y/\sqrt a,-\sqrt ax) (y/a ,−a x),(y/a ,−a x)。之所以横纵坐标分别取不同的符号,是为了保证点表示的唯一性??? 亦即 ε a , d \varepsilon_{a,d} εa,d对应的group G = { ( x , y ) , ( − x , − y ) , ( y / a , − a x ) , ( y / a , − a x ) } G=\{(x,y),(-x,-y),(y/\sqrt a,-\sqrt ax),(y/\sqrt a,-\sqrt ax)\} G={(x,y),(−x,−y),(y/a ,−a x),(y/a ,−a x)}
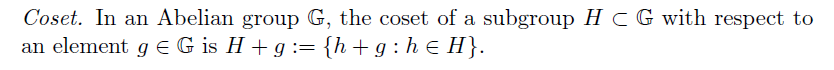 所以相应的coset of H=
{
(
x
,
y
)
,
(
−
x
,
−
y
)
,
(
y
/
a
,
−
a
x
)
,
(
−
y
/
a
,
a
x
)
}
\{(x,y),(-x,-y),(y/\sqrt a,-\sqrt ax),(-y/\sqrt a,\sqrt ax)\}
{(x,y),(−x,−y),(y/a
,−a
x),(−y/a
,a
x)}
所以相应的coset of H=
{
(
x
,
y
)
,
(
−
x
,
−
y
)
,
(
y
/
a
,
−
a
x
)
,
(
−
y
/
a
,
a
x
)
}
\{(x,y),(-x,-y),(y/\sqrt a,-\sqrt ax),(-y/\sqrt a,\sqrt ax)\}
{(x,y),(−x,−y),(y/a
,−a
x),(−y/a
,a
x)}
亦即 P + ε a , d [ 4 ] = { ( x , y ) , ( − x , − y ) , ( y / a , − a x ) , ( − y / a , a x ) } P+\varepsilon_{a,d}[4]=\{(x,y),(-x,-y),(y/\sqrt a,-\sqrt ax),(-y/\sqrt a,\sqrt ax)\} P+εa,d[4]={(x,y),(−x,−y),(y/a ,−a x),(−y/a ,a x)}
1.1.1 Edwards 4-torsion subgroup验证论文《Twisted Edwards Curves Revisited》中有: 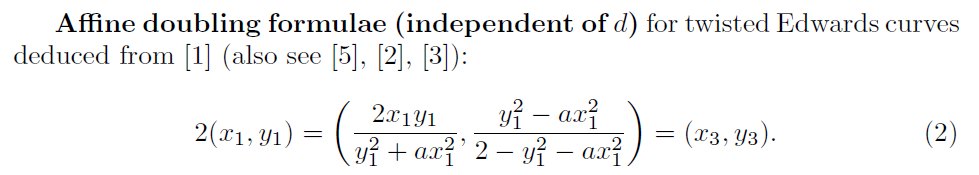 可知,当
(
x
1
,
y
1
)
(x_1,y_1)
(x1,y1)为
(
0
,
1
)
(0,1)
(0,1)或
(
0
,
−
1
)
(0,-1)
(0,−1)时,对应的
2
(
0
,
1
)
=
(
0
,
1
)
=
i
d
e
n
t
i
t
y
p
o
i
n
t
o
f
e
d
w
a
r
d
s
2(0,1)=(0,1)=identity\ point\ of\ edwards
2(0,1)=(0,1)=identity point of edwards,和
2
(
0
,
−
1
)
=
(
0
,
1
)
=
i
d
e
n
t
i
t
y
p
o
i
n
t
o
f
e
d
w
a
r
d
s
2(0,-1)=(0,1)=identity\ point\ of\ edwards
2(0,−1)=(0,1)=identity point of edwards
∴
(
0
,
1
)
(
0
,
−
1
)
为
2
−
t
o
r
s
i
o
n
p
o
i
n
t
\therefore (0,1) (0,-1)为2-torsion\ point
∴(0,1)(0,−1)为2−torsion point
可知,当
(
x
1
,
y
1
)
(x_1,y_1)
(x1,y1)为
(
0
,
1
)
(0,1)
(0,1)或
(
0
,
−
1
)
(0,-1)
(0,−1)时,对应的
2
(
0
,
1
)
=
(
0
,
1
)
=
i
d
e
n
t
i
t
y
p
o
i
n
t
o
f
e
d
w
a
r
d
s
2(0,1)=(0,1)=identity\ point\ of\ edwards
2(0,1)=(0,1)=identity point of edwards,和
2
(
0
,
−
1
)
=
(
0
,
1
)
=
i
d
e
n
t
i
t
y
p
o
i
n
t
o
f
e
d
w
a
r
d
s
2(0,-1)=(0,1)=identity\ point\ of\ edwards
2(0,−1)=(0,1)=identity point of edwards
∴
(
0
,
1
)
(
0
,
−
1
)
为
2
−
t
o
r
s
i
o
n
p
o
i
n
t
\therefore (0,1) (0,-1)为2-torsion\ point
∴(0,1)(0,−1)为2−torsion point
而: 2 ( 1 / a , 0 ) = ( 0 , − 1 ) ⇒ 4 ( 1 / a , 0 ) = 2 ( 0 , − 1 ) = ( 0 , 1 ) = i d e n t i t y p o i n t o f e d w a r d s 2(1/\sqrt a,0)=(0,-1)\Rightarrow 4(1/\sqrt a,0)=2(0,-1)=(0,1)=identity\ point\ of\ edwards 2(1/a ,0)=(0,−1)⇒4(1/a ,0)=2(0,−1)=(0,1)=identity point of edwards 2 ( − 1 / a , 0 ) = ( 0 , − 1 ) ⇒ 4 ( − 1 / a , 0 ) = 2 ( 0 , − 1 ) = ( 0 , 1 ) = i d e n t i t y p o i n t o f e d w a r d s 2(-1/\sqrt a,0)=(0,-1)\Rightarrow 4(-1/\sqrt a,0)=2(0,-1)=(0,1)=identity\ point\ of\ edwards 2(−1/a ,0)=(0,−1)⇒4(−1/a ,0)=2(0,−1)=(0,1)=identity point of edwards ∴ ( 1 / a , 0 ) ( − 1 / a , 0 ) 为 4 − t o r s i o n p o i n t \therefore (1/\sqrt a,0) (-1/\sqrt a,0)为4-torsion\ point ∴(1/a ,0)(−1/a ,0)为4−torsion point
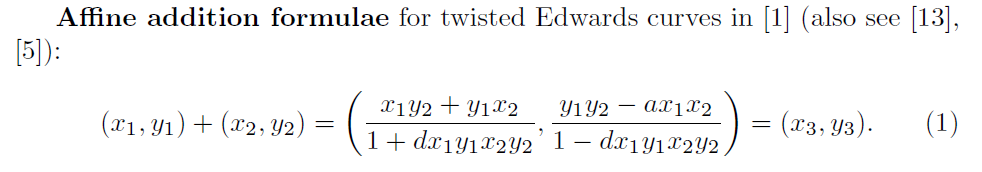 因此有:
(
x
,
y
)
+
(
0
,
−
1
)
=
(
−
x
,
−
y
)
;
(
x
,
y
)
+
(
0
,
1
)
=
(
x
,
y
)
;
(
x
,
y
)
+
(
1
/
a
,
0
)
=
(
y
/
a
,
−
a
x
)
;
(
x
,
y
)
+
(
−
1
/
a
,
0
)
=
(
−
y
/
a
,
a
x
)
(x,y)+(0,-1)=(-x,-y);(x,y)+(0,1)=(x,y);(x,y)+(1/\sqrt a,0)=(y/\sqrt a,-\sqrt ax);(x,y)+(-1/\sqrt a,0)=(-y/\sqrt a,\sqrt ax)
(x,y)+(0,−1)=(−x,−y);(x,y)+(0,1)=(x,y);(x,y)+(1/a
,0)=(y/a
,−a
x);(x,y)+(−1/a
,0)=(−y/a
,a
x) 同理对其它G中的点,做类似的计算。
∴
c
o
s
e
t
o
f
H
=
{
(
x
,
y
)
,
(
−
x
,
−
y
)
,
(
y
/
a
,
−
a
x
)
,
(
−
y
/
a
,
a
x
)
}
\therefore coset\ of\ H=\{(x,y),(-x,-y),(y/\sqrt a,-\sqrt ax),(-y/\sqrt a,\sqrt ax)\}
∴coset of H={(x,y),(−x,−y),(y/a
,−a
x),(−y/a
,a
x)}
因此有:
(
x
,
y
)
+
(
0
,
−
1
)
=
(
−
x
,
−
y
)
;
(
x
,
y
)
+
(
0
,
1
)
=
(
x
,
y
)
;
(
x
,
y
)
+
(
1
/
a
,
0
)
=
(
y
/
a
,
−
a
x
)
;
(
x
,
y
)
+
(
−
1
/
a
,
0
)
=
(
−
y
/
a
,
a
x
)
(x,y)+(0,-1)=(-x,-y);(x,y)+(0,1)=(x,y);(x,y)+(1/\sqrt a,0)=(y/\sqrt a,-\sqrt ax);(x,y)+(-1/\sqrt a,0)=(-y/\sqrt a,\sqrt ax)
(x,y)+(0,−1)=(−x,−y);(x,y)+(0,1)=(x,y);(x,y)+(1/a
,0)=(y/a
,−a
x);(x,y)+(−1/a
,0)=(−y/a
,a
x) 同理对其它G中的点,做类似的计算。
∴
c
o
s
e
t
o
f
H
=
{
(
x
,
y
)
,
(
−
x
,
−
y
)
,
(
y
/
a
,
−
a
x
)
,
(
−
y
/
a
,
a
x
)
}
\therefore coset\ of\ H=\{(x,y),(-x,-y),(y/\sqrt a,-\sqrt ax),(-y/\sqrt a,\sqrt ax)\}
∴coset of H={(x,y),(−x,−y),(y/a
,−a
x),(−y/a
,a
x)}
An Edwards curve is called “complete” if d d d and a d ad ad are nonsquare in F, which also implies that a a a is square. A complete Edwards curve has no points at infi nity, and supports fast addition formulas which are complete in that they compute the correct answer for any two input points. 以下magma脚本可证明,ed25519是完备的Edwards curve:
clear;
q:=2^255-19;
LegendreSymbol(37095705934669439343138083508754565189542113879843219016388785533085940283555,q);// 为-1,即不是域Fq内的平方值
LegendreSymbol(-1,q); //为1,即域Fq内的平方值
Jacobi Quartic curve格式如下: J e , A : t 2 = e s 4 + 2 A s 2 + 1 J_{e,A}:t^2=es^4+2As^2+1 Je,A:t2=es4+2As2+1
当 e = a 2 e=a^2 e=a2时, J e , A J_{e,A} Je,A具有full 2-torsion,即 J [ 2 ] ≅ Z / 2 × Z / 2 J[2]\cong \mathbb{Z}/2\times \mathbb{Z}/2 J[2]≅Z/2×Z/2. 论文《Division Polynomials for Jacobi Quartic Curves》中提到: Jacobi Quartic curve的identity point表示为 ( 0 , 1 ) (0,1) (0,1), ( 0 , − 1 ) (0,-1) (0,−1)为2-torsion point。 J e , A [ 2 ] = { ( 0 , 1 ) , ( 0 , − 1 ) } J_{e,A}[2]=\{(0,1),(0,-1)\} Je,A[2]={(0,1),(0,−1)} 可定义Group H = { ( 0 , 1 ) , ( 0 , − 1 ) } H=\{(0,1),(0,-1)\} H={(0,1),(0,−1)}。
当 e = a 2 e=a^2 e=a2时, t 2 = e s 4 + 2 A s 2 + 1 t^2=es^4+2As^2+1 t2=es4+2As2+1可变形为: ( t a s 2 ) 2 = e ( 1 a s ) 4 + 2 A ( 1 a s ) 2 + 1 (\frac{t}{as^2})^2=e(\frac{1}{as})^4+2A(\frac{1}{as})^2+1 (as2t)2=e(as1)4+2A(as1)2+1 因此, J e , A J_{e,A} Je,A上的点point除可表示为 ( s , t ) , ( − s , − t ) (s,t),(-s,-t) (s,t),(−s,−t)外,还可表示为 ( 1 / a s , − t / a s 2 ) , ( − 1 / a s , t / a s 2 ) (1/as,-t/as^2),(-1/as,t/as^2) (1/as,−t/as2),(−1/as,t/as2)。之所以横纵坐标分别取不同的符号,是为了保证点表示的唯一性???
亦即 J e , A J_{e,A} Je,A对应的group G = { ( s , t ) , ( − s , − t ) , ( 1 / a s , − t / a s 2 ) , ( − 1 / a s , t / a s 2 ) } G=\{(s,t),(-s,-t),(1/as,-t/as^2),(-1/as,t/as^2)\} G={(s,t),(−s,−t),(1/as,−t/as2),(−1/as,t/as2)}
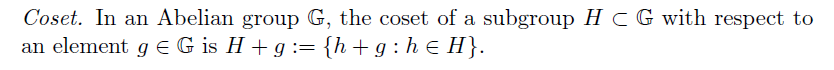 所以相应的coset of H=
{
(
s
,
t
)
,
(
−
s
,
−
t
)
,
(
1
/
a
s
,
−
t
/
a
s
2
)
,
(
−
1
/
a
s
,
t
/
a
s
2
)
}
\{(s,t),(-s,-t),(1/as,-t/as^2),(-1/as,t/as^2)\}
{(s,t),(−s,−t),(1/as,−t/as2),(−1/as,t/as2)}
所以相应的coset of H=
{
(
s
,
t
)
,
(
−
s
,
−
t
)
,
(
1
/
a
s
,
−
t
/
a
s
2
)
,
(
−
1
/
a
s
,
t
/
a
s
2
)
}
\{(s,t),(-s,-t),(1/as,-t/as^2),(-1/as,t/as^2)\}
{(s,t),(−s,−t),(1/as,−t/as2),(−1/as,t/as2)}
对于任意点 P ∈ G P\in G P∈G,有: P + J e , A [ 2 ] = { ( s , t ) , ( − s , − t ) , ( 1 / a s , − t / a s 2 ) , ( − 1 / a s , t / a s 2 ) } P+J_{e,A}[2]=\{(s,t),(-s,-t),(1/as,-t/as^2),(-1/as,t/as^2)\} P+Je,A[2]={(s,t),(−s,−t),(1/as,−t/as2),(−1/as,t/as2)}
以上可理解为: J e , A J e , A [ 2 ] = P + J e , A [ 2 ] = { ( s , t ) , ( − s , − t ) , ( 1 / a s , − t / a s 2 ) , ( − 1 / a s , t / a s 2 ) } \frac{J_{e,A}}{J_{e,A}[2]}=P+J_{e,A}[2]=\{(s,t),(-s,-t),(1/as,-t/as^2),(-1/as,t/as^2)\} Je,A[2]Je,A=P+Je,A[2]={(s,t),(−s,−t),(1/as,−t/as2),(−1/as,t/as2)},任意的点 P ∈ G P\in G P∈G modulo J e , A [ 2 ] J_{e,A}[2] Je,A[2],可实现一定程度的压缩。
在论文《Decaf-Eliminating cofactors through point compression 2015-673》中,任意点 P P P以 ( s , t ) (s,t) (s,t)形式表示,约定 s , t s,t s,t均为非负数,实际仅需 s s s坐标值即可代表任意点 P P P。
1.2.1 Jacobi Quartic curve 2-torsion point验证论文《Jacobi Quartic Curves Revisited》中指出Jacobi Quartic curve point addition的公式为:  J
e
,
A
:
t
2
=
e
s
4
+
2
A
s
2
+
1
J_{e,A}:t^2=es^4+2As^2+1
Je,A:t2=es4+2As2+1相应的double公式为:
2
(
s
1
,
t
1
)
=
(
2
s
1
t
1
1
−
e
s
1
4
,
t
1
2
+
e
s
1
4
t
1
2
+
2
A
s
1
2
+
2
e
A
s
1
6
+
4
e
s
1
4
(
1
−
e
s
1
4
)
2
)
=
(
s
3
,
t
3
)
2(s_1,t_1)=(\frac{2s_1t_1}{1-es_1^4},\frac{t_1^2+es_1^4t_1^2+2As_1^2+2eAs_1^6+4es_1^4}{(1-es_1^4)^2})=(s_3,t_3)
2(s1,t1)=(1−es142s1t1,(1−es14)2t12+es14t12+2As12+2eAs16+4es14)=(s3,t3)
J
e
,
A
:
t
2
=
e
s
4
+
2
A
s
2
+
1
J_{e,A}:t^2=es^4+2As^2+1
Je,A:t2=es4+2As2+1相应的addition公式为:
(
s
1
,
t
1
)
+
(
s
2
+
t
2
)
=
(
s
1
t
2
+
t
1
s
2
1
−
e
s
1
2
s
2
2
,
(
t
1
t
2
+
2
A
s
1
s
2
)
(
1
+
e
s
1
2
s
2
2
)
+
2
e
s
1
s
2
(
s
1
2
+
s
2
2
)
(
1
−
e
s
1
2
s
2
2
)
2
)
=
(
s
3
,
t
3
)
(s_1,t_1)+(s_2+t_2)=(\frac{s_1t_2+t_1s_2}{1-es_1^2s_2^2},\frac{(t_1t_2+2As_1s_2)(1+es_1^2s_2^2)+2es_1s_2(s_1^2+s_2^2)}{(1-es_1^2s_2^2)^2})=(s_3,t_3)
(s1,t1)+(s2+t2)=(1−es12s22s1t2+t1s2,(1−es12s22)2(t1t2+2As1s2)(1+es12s22)+2es1s2(s12+s22))=(s3,t3)
J
e
,
A
:
t
2
=
e
s
4
+
2
A
s
2
+
1
J_{e,A}:t^2=es^4+2As^2+1
Je,A:t2=es4+2As2+1相应的double公式为:
2
(
s
1
,
t
1
)
=
(
2
s
1
t
1
1
−
e
s
1
4
,
t
1
2
+
e
s
1
4
t
1
2
+
2
A
s
1
2
+
2
e
A
s
1
6
+
4
e
s
1
4
(
1
−
e
s
1
4
)
2
)
=
(
s
3
,
t
3
)
2(s_1,t_1)=(\frac{2s_1t_1}{1-es_1^4},\frac{t_1^2+es_1^4t_1^2+2As_1^2+2eAs_1^6+4es_1^4}{(1-es_1^4)^2})=(s_3,t_3)
2(s1,t1)=(1−es142s1t1,(1−es14)2t12+es14t12+2As12+2eAs16+4es14)=(s3,t3)
J
e
,
A
:
t
2
=
e
s
4
+
2
A
s
2
+
1
J_{e,A}:t^2=es^4+2As^2+1
Je,A:t2=es4+2As2+1相应的addition公式为:
(
s
1
,
t
1
)
+
(
s
2
+
t
2
)
=
(
s
1
t
2
+
t
1
s
2
1
−
e
s
1
2
s
2
2
,
(
t
1
t
2
+
2
A
s
1
s
2
)
(
1
+
e
s
1
2
s
2
2
)
+
2
e
s
1
s
2
(
s
1
2
+
s
2
2
)
(
1
−
e
s
1
2
s
2
2
)
2
)
=
(
s
3
,
t
3
)
(s_1,t_1)+(s_2+t_2)=(\frac{s_1t_2+t_1s_2}{1-es_1^2s_2^2},\frac{(t_1t_2+2As_1s_2)(1+es_1^2s_2^2)+2es_1s_2(s_1^2+s_2^2)}{(1-es_1^2s_2^2)^2})=(s_3,t_3)
(s1,t1)+(s2+t2)=(1−es12s22s1t2+t1s2,(1−es12s22)2(t1t2+2As1s2)(1+es12s22)+2es1s2(s12+s22))=(s3,t3)
⇒ 2 ( 0 , − 1 ) = ( 0 , 1 ) = i d e n t i t y p o i n t o f J a c o b i Q u a r t i c \Rightarrow 2(0,-1)=(0,1)=identity\ point\ of\ Jacobi\ Quartic ⇒2(0,−1)=(0,1)=identity point of Jacobi Quartic ∴ ( 0 , − 1 ) 为 2 − t o r s i o n p o i n t . \therefore (0,-1)为2-torsion\ point. ∴(0,−1)为2−torsion point.
⇒ ( s , t ) + ( 0 , − 1 ) = ( − s , − t ) ; ( 1 / a s , − t / a s 2 ) + ( 0 , − 1 ) = ( − 1 / a s , t / a s 2 ) \Rightarrow (s,t)+(0,-1)=(-s,-t);(1/as,-t/as^2)+(0,-1)=(-1/as,t/as^2) ⇒(s,t)+(0,−1)=(−s,−t);(1/as,−t/as2)+(0,−1)=(−1/as,t/as2) ∴ c o s e t o f H = { ( s , t ) , ( − s , − t ) , ( 1 / a s , − t / a s 2 ) , ( − 1 / a s , t / a s 2 ) } \therefore coset\ of\ H=\{(s,t),(-s,-t),(1/as,-t/as^2),(-1/as,t/as^2)\} ∴coset of H={(s,t),(−s,−t),(1/as,−t/as2),(−1/as,t/as2)}
1.3 Twisted Edwards curve与Jacobi Quartic curve之间的N-isogenous关系根据书《Elliptic Curves Number Theory And Cryptography 2n》中定义: 
 Twisted Edwards curves的affine坐标系表示为:
ε
a
,
d
:
=
{
(
x
,
y
)
∈
P
2
(
F
)
:
a
∗
x
2
+
y
2
=
1
+
d
∗
x
2
∗
y
2
}
\varepsilon_{a,d}:=\{(x,y)\in P^2(F):a*x^2+y^2=1+d*x^2*y^2\}
εa,d:={(x,y)∈P2(F):a∗x2+y2=1+d∗x2∗y2} Jacobi Quartic curve格式如下:
J
a
2
,
a
−
2
d
:
t
2
=
a
2
s
4
+
2
(
a
−
2
d
)
s
2
+
1
J_{a^2,a-2d}:t^2=a^2s^4+2(a-2d)s^2+1
Ja2,a−2d:t2=a2s4+2(a−2d)s2+1 两者之间的映射关系为:
(
x
,
y
)
↦
(
s
,
t
)
:
s
=
x
y
,
t
=
2
−
y
2
−
a
x
2
y
2
(x,y)\mapsto (s,t):s=\frac{x}{y},t=\frac{2-y^2-ax^2}{y^2}
(x,y)↦(s,t):s=yx,t=y22−y2−ax2
Twisted Edwards curves的affine坐标系表示为:
ε
a
,
d
:
=
{
(
x
,
y
)
∈
P
2
(
F
)
:
a
∗
x
2
+
y
2
=
1
+
d
∗
x
2
∗
y
2
}
\varepsilon_{a,d}:=\{(x,y)\in P^2(F):a*x^2+y^2=1+d*x^2*y^2\}
εa,d:={(x,y)∈P2(F):a∗x2+y2=1+d∗x2∗y2} Jacobi Quartic curve格式如下:
J
a
2
,
a
−
2
d
:
t
2
=
a
2
s
4
+
2
(
a
−
2
d
)
s
2
+
1
J_{a^2,a-2d}:t^2=a^2s^4+2(a-2d)s^2+1
Ja2,a−2d:t2=a2s4+2(a−2d)s2+1 两者之间的映射关系为:
(
x
,
y
)
↦
(
s
,
t
)
:
s
=
x
y
,
t
=
2
−
y
2
−
a
x
2
y
2
(x,y)\mapsto (s,t):s=\frac{x}{y},t=\frac{2-y^2-ax^2}{y^2}
(x,y)↦(s,t):s=yx,t=y22−y2−ax2
即 ϕ ^ ( x , y ) = ( x y , 2 − y 2 − a x 2 y 2 ) : ε a , d ↦ J a 2 , a − 2 d \hat{\phi } (x,y)=(\frac{x}{y},\frac{2-y^2-ax^2}{y^2}): \varepsilon_{a,d}\mapsto J_{a^2,a-2d} ϕ^(x,y)=(yx,y22−y2−ax2):εa,d↦Ja2,a−2d
( s , t ) ↦ ( x , y ) : x = 2 s 1 + a s 2 , y = 1 − a s 2 t (s,t) \mapsto (x,y):x=\frac{2s}{1+as^2},y=\frac{1-as^2}{t} (s,t)↦(x,y):x=1+as22s,y=t1−as2
即 ϕ ( s , t ) = ( 2 s 1 + a s 2 , 1 − a s 2 t ) : J a 2 , a − 2 d ↦ ε a , d \phi (s,t)=(\frac{2s}{1+as^2},\frac{1-as^2}{t}): J_{a^2,a-2d}\mapsto \varepsilon_{a,d} ϕ(s,t)=(1+as22s,t1−as2):Ja2,a−2d↦εa,d
∵ 2 ( s 1 , t 1 ) = ( 2 s 1 t 1 1 − e s 1 4 , t 1 2 + e s 1 4 t 1 2 + 2 A s 1 2 + 2 e A s 1 6 + 4 e s 1 4 ( 1 − e s 1 4 ) 2 ) = ( x y , 2 − y 2 − a x 2 y 2 ) , 当 x = 2 s 1 + a s 2 , y = 1 − a s 2 t \because 2(s_1,t_1)=(\frac{2s_1t_1}{1-es_1^4},\frac{t_1^2+es_1^4t_1^2+2As_1^2+2eAs_1^6+4es_1^4}{(1-es_1^4)^2})=(\frac{x}{y},\frac{2-y^2-ax^2}{y^2}),当x=\frac{2s}{1+as^2},y=\frac{1-as^2}{t} ∵2(s1,t1)=(1−es142s1t1,(1−es14)2t12+es14t12+2As12+2eAs16+4es14)=(yx,y22−y2−ax2),当x=1+as22s,y=t1−as2
∴ [ 2 ] : J a 2 , a − 2 d ↦ ε a , d \therefore [2]:J_{a^2,a-2d}\mapsto \varepsilon_{a,d} ∴[2]:Ja2,a−2d↦εa,d
∴ \therefore ∴ J a 2 , a − 2 d J_{a^2,a-2d} Ja2,a−2d为 ε a , d \varepsilon_{a,d} εa,d的2-isogenous。
根据推论: 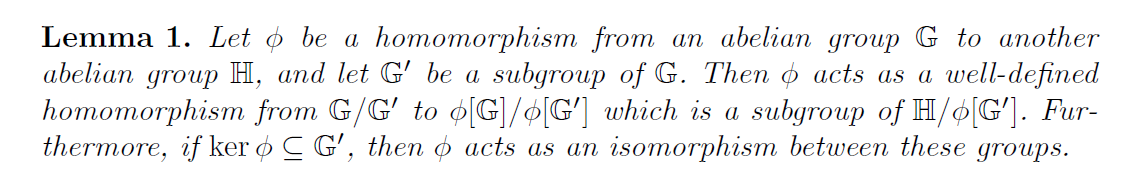 ∴
J
J
[
2
]
≅
ϕ
(
J
)
ϕ
(
J
[
2
]
)
≅
[
2
]
(
ε
)
ε
[
2
]
\therefore \frac{J}{J[2]}\cong \frac{\phi(J)}{\phi(J[2])}\cong \frac{[2](\varepsilon)}{\varepsilon[2]}
∴J[2]J≅ϕ(J[2])ϕ(J)≅ε[2][2](ε)
∴
J
J
[
2
]
≅
ϕ
(
J
)
ϕ
(
J
[
2
]
)
≅
[
2
]
(
ε
)
ε
[
2
]
\therefore \frac{J}{J[2]}\cong \frac{\phi(J)}{\phi(J[2])}\cong \frac{[2](\varepsilon)}{\varepsilon[2]}
∴J[2]J≅ϕ(J[2])ϕ(J)≅ε[2][2](ε)
- 当曲线的cofactor为4时,有$ # ε ( F p ) = 4 ∗ l \#\varepsilon(F_p)=4*l #ε(Fp)=4∗l,而 [ 2 ] ( ε ) ε [ 2 ] \frac{[2](\varepsilon)}{\varepsilon[2]} ε[2][2](ε)的order即为素数 ( 4 l / 2 ) / 2 = l (4l/2)/2=l (4l/2)/2=l。因此此时即可避免cofactor=4的small-subgroup的影响。
- 当曲线的cofactor为8时,有$ # ε ( F p ) = 8 ∗ l \#\varepsilon(F_p)=8*l #ε(Fp)=8∗l,有 [ 2 ] ( ε [ 8 ] ) = ε [ 4 ] [2](\varepsilon[8])=\varepsilon[4] [2](ε[8])=ε[4], ε [ 4 ] ⊆ [ 2 ] ( ε ) \varepsilon[4]\subseteq [2](\varepsilon) ε[4]⊆[2](ε),于是有 [ 2 ] ( ε ) ε [ 4 ] \frac{[2](\varepsilon)}{\varepsilon[4]} ε[4][2](ε)的order即为 ( 8 l / 2 ) / 4 = l (8l/2)/4=l (8l/2)/4=l。
所以,当曲线的cofactor为8时,接下来是要将points从 ε ε [ 4 ] \frac{\varepsilon}{\varepsilon[4]} ε[4]ε扭转到 ε ε [ 2 ] \frac{\varepsilon}{\varepsilon[2]} ε[2]ε。
根据1.1节有: ε a , d [ 4 ] = { ( 0 , 1 ) , ( 1 / a , 0 ) , ( 0 , − 1 ) , ( − 1 / a , 0 ) } ; \varepsilon_{a,d}[4]=\{(0,1),(1/\sqrt a,0),(0,-1), (-1/\sqrt a, 0)\}; εa,d[4]={(0,1),(1/a ,0),(0,−1),(−1/a ,0)}; 其中 ( 0 , − 1 ) , ( 0 , 1 ) (0,-1),(0,1) (0,−1),(0,1)为2-torsion point, ( 1 / a , 0 ) , ( − 1 / a , 0 ) (1/\sqrt a,0),(-1/\sqrt a, 0) (1/a ,0),(−1/a ,0)为4-torsion point。
P + ε a , d [ 4 ] = { ( x , y ) , ( − x , − y ) , ( y / a , − a x ) , ( − y / a , a x ) } P+\varepsilon_{a,d}[4]=\{(x,y),(-x,-y),(y/\sqrt a,-\sqrt ax),(-y/\sqrt a,\sqrt ax)\} P+εa,d[4]={(x,y),(−x,−y),(y/a ,−a x),(−y/a ,a x)}
( x , y ) + ( 0 , − 1 ) = ( − x , − y ) ; ( x , y ) + ( 0 , 1 ) = ( x , y ) ; ( x , y ) + ( 1 / a , 0 ) = ( y / a , − a x ) ; ( x , y ) + ( − 1 / a , 0 ) = ( − y / a , a x ) (x,y)+(0,-1)=(-x,-y);(x,y)+(0,1)=(x,y);(x,y)+(1/\sqrt a,0)=(y/\sqrt a,-\sqrt ax);(x,y)+(-1/\sqrt a,0)=(-y/\sqrt a,\sqrt ax) (x,y)+(0,−1)=(−x,−y);(x,y)+(0,1)=(x,y);(x,y)+(1/a ,0)=(y/a ,−a x);(x,y)+(−1/a ,0)=(−y/a ,a x) 注意上面公式中:
-
当要求 x y > 0 xy>0 xy>0时,加法中对应的均为2-torsion point ( 0 , 1 ) , ( 0 , − 1 ) (0,1),(0,-1) (0,1),(0,−1),所以,此时相当于求的是: P + ε a , d [ 2 ] = { ( x , y ) , ( − x , − y ) } P+\varepsilon_{a,d}[2]=\{(x,y),(-x,-y)\} P+εa,d[2]={(x,y),(−x,−y)}。 亦即由此实现由 ε ε [ 4 ] \frac{\varepsilon}{\varepsilon[4]} ε[4]ε扭转到 ε ε [ 2 ] \frac{\varepsilon}{\varepsilon[2]} ε[2]ε。
-
当 x y < 0 xy<0 xy1的椭圆曲线(如Curve25519等)的兼容(含Curve25519 cofactor的sage验证) [7] https://ristretto.group/details/curve_models.html



