- RSA-based Vector Commitment:当前的主要实现有https://github.com/cambrian/accumulator和https://github.com/dignifiedquire/rust-accumulators
- merkle tree based vector commitment:当前的主要实现有https://github.com/0xProject/OpenZKP/tree/master/crypto/merkle-tree
- pedersen vector commitment:主要实现有https://github.com/mimblewimble/rust-secp256k1-zkp/blob/master/src/pedersen.rs
- cosmos vector commitment:有提案,暂未实现。https://github.com/cosmos/ics/tree/master/spec/ics-023-vector-commitments
accumulator做vector commit的关键点在于: 1)将vector转换位bit vector表示,也就是说vector中只有0,1值。 2)根据vector中的1值创建co-prime vector。co-prime vector的prime元素是通过位置来映射的。如https://github.com/dignifiedquire/rust-accumulators/blob/master/src/vc/binary.rs中的map_i_to_p_i函数,保证了prover和verifier对于指定的位置
i
i
i,都有唯一的prime
p
i
p_i
pi与之对应。 3)prove时,根据需要open的位置
i
i
i值为0或者1来确定是做non-membership proof还是做membership proof。
polynomial commitment: 仅用于证明prover知道某个 n n n阶函数 f 1 ( X ) f_1(X) f1(X),使得其在某点 x x x的返回值确实为 v a l val val,使得 v a l = = f 1 ( x ) val==f_1(x) val==f1(x)成立。但是,并不能证明 n n n阶函数 f 1 ( X ) f_1(X) f1(X)的唯一性,存在另外的函数 f 2 ( X ) f_2(X) f2(X),使得 v a l = = f 2 ( x ) val==f_2(x) val==f2(x)亦成立。除非用 n n n个不同的 x x x值去challenge prover,否则根本无法唯一确定prover所知道的函数。 怎么将polynomial commitment用于vector commiment呢?可以open指定的系数,同时不需要通过 n n n个challenge来唯一确定????【 ⇒ \Rightarrow ⇒ 具体见博客vector commitment 中提到的2015年论文《Composable & Modular Anonymous Credentials:Definitions and Practical Constructions》第三节中提到了通过构建Lagrange basis polynomial来实现vector commitment的算法。】
2. 原理&性能 2.1 https://github.com/dignifiedquire/rust-accumulators原理&性能主要基于2018年论文《Batching Techniques for Accumulators with Applications to IOPs and Stateless Blockchains》——是基于strong RSA assumption in groups of unknown order来实现的,其基本原理为: 针对bit vector
m
⃗
=
{
m
1
,
m
2
,
.
.
.
,
m
n
}
,
m
i
∈
{
0
,
1
}
\vec{m}=\{m_1,m_2,...,m_n\},m_i\in\{0,1\}
m
={m1,m2,...,mn},mi∈{0,1},构建一个相应的co-prime【co-prime这个属性很好,可以保证某个数值不可能在两个以上的位置存在,否则与co-prime矛盾。】 vector
p
⃗
=
{
p
1
,
p
2
,
.
.
.
,
p
l
}
\vec{p}=\{p_1,p_2,...,p_l\}
p
={p1,p2,...,pl},
m
i
=
0
m_i=0
mi=0的个数为
n
−
l
n-l
n−l。若
m
i
=
1
m_i=1
mi=1,则提供an inclusion proof of
p
i
p_i
pi;若
m
i
=
0
m_i=0
mi=0,则提供an exclusion proof of
p
i
p_i
pi。引申到更通用的情况是,任意的vector,其元素可由
λ
−
b
i
t
s
\lambda-bits
λ−bits组成,相应的open可引申为
λ
\lambda
λ个位置的batch opening。 
cargo bench性能如下: 
主要也是基于2018年论文《Batching Techniques for Accumulators with Applications to IOPs and Stateless Blockchains》和2007年论文《Universal Accumulators with Efficient Nonmembership Proofs》来实现的。 其代码实现性能优于2.1,但是没有充分利用多核CPU的能力,计算压力仍然集中在单个CPU上: 
cosmos将vector commitment中划分了三个角色: 1)manager:负责从commitment中添加或删除元素; 2)prover:负责生成membership proof或non membership proof; 3)verifier:验证proof。 这其中提到了2017年论文《Accumulators with Applications to Anonymity-Preserving Revocation》中,提出借助密码学累加器来实现匿名撤销算法。在累加器中添加白名单信息,通过membership proof和 nonmembership proof来证明 同时支持元素添加和删除的累加器叫做动态累加器。常用的动态累加器有:
- 基于Merkle hash trees。
- 基于RSA。
- 基于bilinear maps。

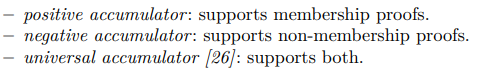
 并对多种累加器的进行了对比。
并对多种累加器的进行了对比。 
参考资料: [1] 2013年论文《Vector Commitments and their Applications》 [2] 2017年论文《Accumulators with Applications to Anonymity-Preserving Revocation》 [3] 2018年论文《Batching Techniques for Accumulators with Applications to IOPs and Stateless Blockchains》 [4] https://github.com/cosmos/ics/tree/master/spec/ics-023-vector-commitments [5] https://github.com/filecoin-project/devgrants/blob/master/rfps/rfp-rsa-vector-commitments.md [6] Confidential Transactions from Basic Principles [7] https://github.com/filecoin-project/specs/blob/121-sector-id-as-input-to-commit-sector/notes/porep-with-vc.md [8] https://github.com/cryptoeconomicslab/plasma-chamber/issues/164 [9] https://github.com/filecoin-project/research/issues/131 [10] https://github.com/filecoin-project/research/issues/108 [11] 博客Class Groups for Cryptographic Accumulators



