向量的Hadamard product VS Inner product

1. 定义

向量的Hadmard product表示为： a ⃗ ⊙ b ⃗ = ( a 0 b 0 , a 1 b 1 , a 2 b 2 , … , a n b n ) \vec{a} \odot \vec{b}=(a_0b_0,a_1b_1,a_2b_2,…,a_nb_n) a ⊙b =(a0​b0​,a1​b1​,a2​b2​,…,an​bn​) 向量的Inner product表示为： < a ⃗ , b ⃗ > = ∑ i = 0 n a i b i =\sum_{i=0}^{n}a_ib_i =∑i=0n​ai​bi​

注意，Hadmard product与Inner product的转换可为： < a ⃗ , b ⃗ > = ∑ i = 0 n a i b i = < 1 ⃗ , a ⃗ ⊙ b ⃗ > ， 其 中 1 ⃗ = ( 1 , 1 , 1 , . . . . , 1 ) =\sum_{i=0}^{n}a_ib_i=，其中\vec{1}=(1,1,1,....,1) =∑i=0n​ai​bi​=，其中1 =(1,1,1,....,1) 同时有： a ⃗ = a ⃗ ⊙ 1 ⃗ ， 其 中 1 ⃗ = ( 1 , 1 , 1 , . . . . , 1 ) \vec{a} =\vec{a} \odot \vec{1}，其中\vec{1}=(1,1,1,....,1) a =a ⊙1 ，其中1 =(1,1,1,....,1)

2. Inner product 证明

Inner product证明参见博客Zero-knowledge inner product argument（IPA）。

3. Hadamard product证明

EIGamal Encryption具有乘法同态特性。

在2012年论文《Efficient Zero-Knowledge Argument for Correctness of a Shuffle》 第5章节中，提及了Hadamard product argument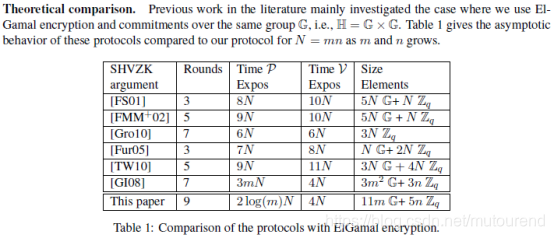： 参考资料： [1] 2012年论文《Efficient Zero-Knowledge Argument for Correctness of a Shuffle》