LDC——Locally Decodable Code

1. 纠错码

1）理想的传输模型示例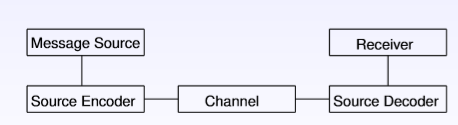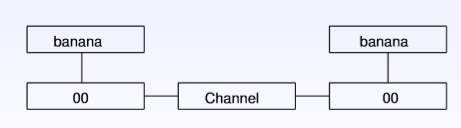： 2）实际的传输模型为： 3）带纠错功能的传输模型为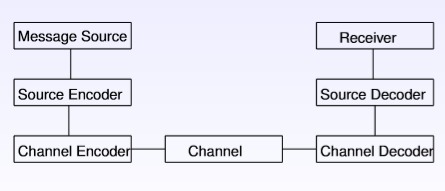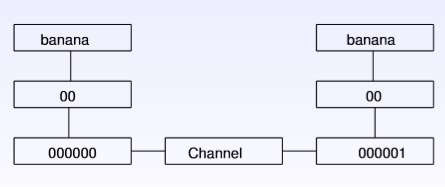： 纠错码(error correcting code)，在传输过程中发生错误后能在收端自行发现或纠正的码。纠错码常用于保证信息在noisy channel的可靠传输以及保证信息在媒介上的可靠存储（可能会随着时间partially corrupted或者说相应的reading device is subject to errors）。 仅用来发现错误的码一般常称为检错码。检错码与其他手段结合使用，可以纠错。 为使一种码具有检错或纠错能力，须对原码字增加多余的码元，以扩大码字之间的差别 ，即把原码字按某种规则变成有一定剩余度（见信源编码）的码字，并使每个码字的码之间有一定的关系。关系的建立称为编码。码字到达收端后，可以根据编码规则是否满足以判定有无错误。当不能满足时，按一定规则确定错误所在位置并予以纠正。纠错并恢复原码字的过程称为译码。

纠错码的典型应用是：将message切分为小的blocks，每个block单独编码，当只对某部分信息感兴趣时，可仅解码相应的部分即可。这种策略的优点是：可保证random-access retrieval of information的效率。缺点是：抗噪能力比较弱，哪怕仅有一个block completely corrupted了，相应的信息也就完全丢失了。

提高抗噪能力的一种办法是：对整个message使用纠错码进行编码（encode the whole message into a single codeword of an error-correcting code）。这种策略抗噪能力是增强了，但是当某人仅对某一部分信息感兴趣时，也需要恢复整个message。当面对的是现代的大数据集时，对应的解码复杂度也是令人难以接受的。

1.1 线性纠错码Linear code

其中的 k k k为the dimension of the code， n n n为the block length of the code。Linear code需要用 n n n个符号来传递 k k k长的message，相应的效率 R = k / n R=k/n R=k/n。 A linear code of length n n n， dimension k k k，and minimum distance d d d will be called an [ n , k , d ] [n,k,d] [n,k,d] code. 其中 d = m i n   d i s t ( u ⃗ , v ⃗ ) = m i n   w t ( u ⃗ , v ⃗ ) , w h e r e   u ⃗ ! = v ⃗ d=min\ dist(\vec{u},\vec{v})=min\ wt(\vec{u},\vec{v}), where\ \vec{u}!=\vec{v} d=min dist(u ,v )=min wt(u ,v ),where u !=v 。

最小距离 d d d与可correct errors的关系为：

maximum likelihood decoding: 最大释然解码。 nearest neighbor decoding：最近邻解码。 由于error vector e ⃗ \vec{e} e 未知，在实际解码时，若 k k k值小，可采用暴力解码的方式将received vector y ⃗ \vec{y} y ​与 2 k 2^k 2k个可能的 x ⃗ \vec{x} x 对比，找到最接近的值。但是当 k k k值很大时，暴力解码就不实用了。

1.2 nonlinear code

其中的 M M M可表示为 M = A ( n , d ) M=A(n,d) M=A(n,d)。

线性与非线性code的表示方法是有差异的。用圆括号()表示的code可为linear或nonlinear，而用中括号[]表示的就是linear code。 linear code [ n , k , d ] [n,k,d] [n,k,d]也可表示为 ( n , 2 k , d ) (n, 2^k,d) (n,2k,d)。 在相同的 d d d的情况下，若希望最终编码的数量 M M M尽可能多，可以用nonlinear code。

常见的nonlinear code有Hadamard code

1.2.1 Hadamard code

Hadamard matrix定义如下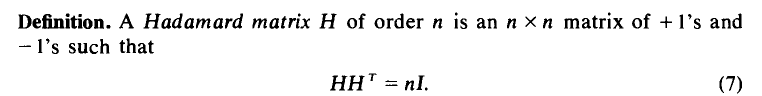： Normalized Hadamard matric如： 若a Hadamard matrix H H H of order n n n exists, then n n n is 1, 2 or a multiple of 4.

经典的Hadmard code是将 n n n-bit messages编码为 2 n 2^n 2n-bit codewords。 由此可知，Hadmard code的query complexity为2，codeword length exponential in the message length.

C H A D C_{HAD} CHAD​的译码流程为： C H A D C_{HAD} CHAD​为2-query ( 2 , δ , 2 δ ) (2,\delta,2\delta) (2,δ,2δ)-LDC，证明如下：

上图中的译码过程，会恢复出所有的原码。当仅需要恢复一个原码而不是完整的所有原码时，---->于是有了LDC（Locally Decodable Code）。

2. LDC

Locally DECODABLE CODE是纠错码的一种，LDC既满足了抗噪性的要求，同时也能提供高效的random-access retrieval。（ allowing reliablereconstruction of an arbitrary bit of the message from looking at only a small number of randomly chosen codeword bits） LDC牺牲了码字效率，需要更长的码字长度。 LDC不仅可用于可靠传输和可靠存储，还可用于其它领域，如：cryptography, complexity theory, data structures, derandomization, and the theory of fault tolerant computation.

Locally decodable codes can be seen as the combinatorial analogs of self-correctors [70, 21] that have been studied in complexity theory in the late 1980s. LDCs were also explicitly discussed in the PCP literature in early 1990s, most notably in [6, 88, 80]. However the fifirst formal defifinition of LDCs was given only in 2000 by Katz and Trevisan [64]. See also Sudan et al. [90]. Since then the study of LDCs has grown into a fairly broad fifield.

2.1 LDC定义

LDC的具体定义如下： 根据以上定义可知，对于 k k k-bit长的message，编码后为 q − q- q−进制字母表的情况，我们希望 r （ 代 表 q u e r y 次 数 ， r < < k ） , N （ 代 表 编 码 后 的 长 度 ） , ϵ （ 代 表 解 码 准 确 率 ） r（代表query次数，r