Introduction to Coding Theory 1999版本

1. 背景知识

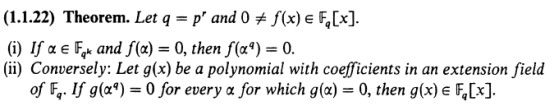
quotient field分式域：在抽象代数中，分式环或分式域是包含一个整环的最小域，典型的例子是有理数域之于整数环。 residue class的定义为: the set of elements (such as integers) that leave the same remainder when divided by a given modulus 因此有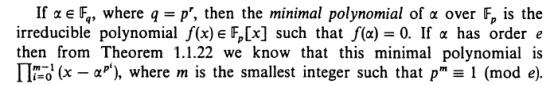： 根据如下定理，有 e = q − 1 e=q-1 e=q−1：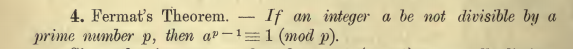

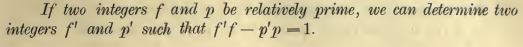
Galois Field定义中， p p p必须为prime且 P ( x ) P(x) P(x)为irreducible modulo p p p。根据上图公式3）中，存在 p n p^n pn distinct classes，这 p n p^n pn个classes of residues 形成的就叫做a Galois Field of order p n p^n pn。 当且仅当 p p p必须为prime且 P ( x ) P(x) P(x)为irreducible modulo p p p时，存在由 p n p^n pn classes of residues moduli p p p and P ( x ) P(x) P(x)形成的域。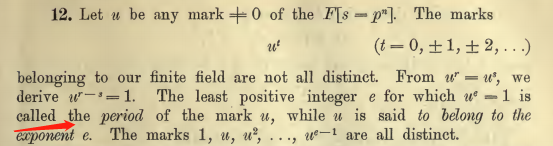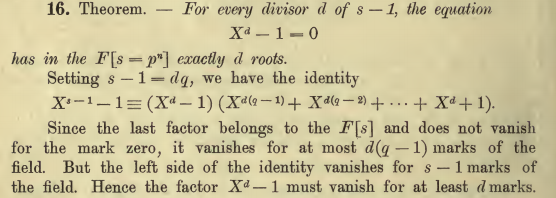 举例如下： 根据上图知道， F [ p n ] F[p^n] F[pn]中不为0的元素有 p n − 1 p^n-1 pn−1个，故而有 e ∣ p n − 1 e|p^n-1 e∣pn−1，即 p n − 1 p^n-1 pn−1为 e e e的倍数，详细的定理如下： 结合Dickson 1901版本书籍《Linear groups》第6条和第13条定义，就很容易理解1999版本书籍《Introduction to Coding Theory》中的1.1.23 example了：

2. Irreducible polynomial的构建

原则上来说，任意degree r r r的irreducible polynomial都应该是存在的。 下图所述是一种直观的寻找irreducible polynomial的方法：首先构建所有degree为1的polynomial 集 P 1 P_1 P1​，由 P 1 P_1 P1​集合中任意两两相乘形成的degree为2的polynomial集 P 2 ′ P_2' P2′​，不在 P 2 ′ P_2' P2′​集中的degree为2的polynomial即为irreducible的。以此类推。 该方法尽管直观，但当degree更高时，效率不够高。 若需找irreducible polynomials over F 2 F_2 F2​ of arbitrarily high degree，可根据如下推论来实现：

3. Quadratic Residues

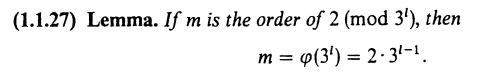
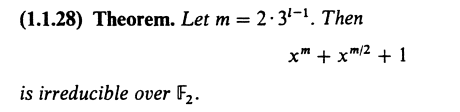
The integers k k k with 0 < k < p 0