Progression-Free Sets and Sublinear Pairing-Based Non-Interactive Zero-Knowledge Arguments

1. 背景知识

在Groth 2010年论文《Short Pairing-based Non-interactive Zero-Knowledge Arguments》论文的基础上，Lipmaa 2012年论文《Progression-Free Sets and Sublinear Pairing-Based Non-Interactive Zero-Knowledge Arguments 》中指出： NIZK proofs无法在无random oracles（如Fiat-Shamir heuristics）或trusted setup（如common reference string）的情况下构建成功。如[BFM88]论文中展示了如何通过common reference string (CRS) model来构建NIZK proofs。

在减少communication complexity和verifier’s computational complexity这两方面，有大量的文献做了研究。

相比于Groth 2010论文，Lipmaa取得了如下进展： 主要特点为：

• 采用了非对称pairing（运算效率更高），而不是对称pairing；

• 采用了更弱的安全假设—— Power Symmetric Discrete Logarithm，而不是 Power Computational Diffifie-Hellman。本论文主要基于两个assumption: computational assumption( Λ − P S D L ^ \hat{\Lambda-PSDL} Λ−PSDL^​)和knowledge assumption( Λ − P K E \Lambda-PKE Λ−PKE)，而Groth10中采用的是 [ a n 2 ] − P K E [an^2]-PKE [an2]−PKE和 [ a n 2 ] − C P D H [an^2]-CPDH [an2]−CPDH假设。

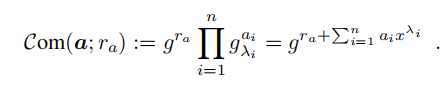Lipmaa 2012的改进流程如下： 1）将 a ⃗ , b ⃗ , c ⃗ \vec{a},\vec{b},\vec{c} a ,b ,c 的commit key缩小统一均为 g λ 1 , . . . , g λ n g_{\lambda_1}, ..., g_{\lambda_n} gλ1​​,...,gλn​​： 从而使构建的 F ( x ) F(x) F(x)多项式的最高阶不大于 2 λ n 2\lambda_n 2λn​，CRS大小 ∣ Λ ^ ∣ < 2 λ n |\hat{\Lambda}|