Lipmaa和Bingsheng Zhang 2012年同时期论文《A More Efficient Computationally Sound Non-Interactive Zero-Knowledge Shuffle Argument*》，要点为：
- 非 random-oracle based的shuffle argument。【In a shuffle argument, the prover proves that two tuples of randomized ciphertexts encrypt the same multiset of plaintexts.】
- zero argument。
- 1-sparsity argument。
- 基于zero argument和1-sparsity argument构建的permutation matrix argument。
- 基于的假设有：knowledge BBS cryptosystem、DLIN assumption以及power symmetric discrete logarithm(PSDL) assumption.【The PSDL assumption is much more standard(-looking) than the SPA and PPA assumptions from [GL07].】
Shuffle argument的历史情况：
- Groth and Ishai [GI08] 的communication复杂度为 Θ ( n 2 / 3 ) \Theta (n^{2/3}) Θ(n2/3)。
- Groth [Gro09] 的communication复杂度为 Θ ( n 1 / 2 ) \Theta (n^{1/2}) Θ(n1/2)。
- Bayer and Groth [BG12] 的communication复杂度为 Θ ( n 1 / 2 ) \Theta (n^{1/2}) Θ(n1/2)。
Permutation matrix为每行每列仅有一个‘1’值的Boolean matrix。 ⇒ \Rightarrow ⇒A matrix is a permutation matrix iff its every column sums to 1 and its every row has exactly one non-zero element.
论文研究情况：
- 论文[FS01]等中，Prover对permutation matrix进行commit，同时提供一份有效的permutation matrix argument。
- 论文Terelius and Wikstr¨om [TW10]中，基于“A matrix is a permutation matrix iff its every column sums to 1 and its every row has exactly one non-zero element.“事实，构建了interactive permutation matrix. 使用了Schwartz-Zippel lemma。
- 本论文基于的事实为：a matrix is a permutation matrix exactly if every column sums to 1 and every row has at most one non-zero element. 且不采用Schwartz-Zippel lemma，故而不需要基于random oracle model来实现NIZK。
Zero argument，即prover can open the given commitment to the zero tuple，可理解为Groth[10]中的restriction argument的特例化，即prover知道knowledge of the discrete logarithm. 
A vector a ∈ Z p n a\in Z_p^n a∈Zpn is k k k-sparse, if it has at most k k k non-zero coefficients. 可认为，zero argument为0-sparsity argument.
1-sparsity argument，即prover can open the given commitment to
a
⃗
=
(
a
1
,
.
.
.
,
a
n
)
\vec{a}=(a_1,...,a_n)
a
=(a1,...,an)，其中最多只有一个
a
i
a_i
ai为非零值。 可转换为证明：
a
i
a
j
=
0
a_ia_j=0
aiaj=0, for every
i
,
j
∈
[
n
]
,
a
n
d
i
!
=
j
.
i,j\in[n],\ and\ i!=j.
i,j∈[n], and i!=j. 
根据Lip[12]可知，the discrete logartihm of the non-interactive argument为： F ( x ) = F c o n ( x ) + F π ( x ) F(x)=F_{con}(x)+F_{\pi}(x) F(x)=Fcon(x)+Fπ(x)，其中 x x x为secret key。
- F c o n ( x ) F_{con}(x) Fcon(x)多项式中，对于honest prover来说，每个constraint均只有1个monomial。在论文Lip[12]中，其constraints的数量为线性的：for any i i i, a i ⋅ b i = c i a_i\cdot b_i=c_i ai⋅bi=ci，而在本论文1-sparsity argument中，其constraints数量为quadratic的：for any two different coefficients a i a_i ai and a j a_j aj, a i ⋅ a j = 0 a_i\cdot a_j=0 ai⋅aj=0。
- F π ( x ) F_{\pi}(x) Fπ(x)多项式中，Lip[12]论文中的monomials为quasilinear的（ O ( n 2 2 2 log 2 n ) O(n2^{2\sqrt{2\log_2n}}) O(n222log2n )），而在1-sparsity argument中为linear的。1-sparsity argument与Lip[12]中的argument相比，其CRS length和prover’s computational complexity均更低。
以上1-sparity argument为非perfectly zero-knwoledge的，原因为： 
其中的
P
i
⃗
\vec{P_i}
Pi
即为permutation matrix
P
P
P 的第
i
i
i行。 
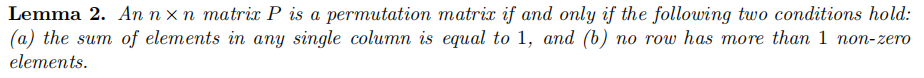
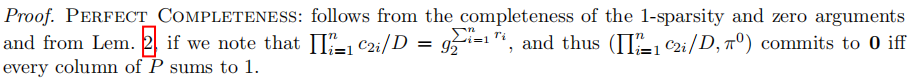
该new shuffle argument具有perfect zero-knowledge。 
