Practical Verifiable Encryption and Decryption of Discrete Logarithms 学习笔记

1 引言

Jan Camenisch 和 Victor Shoup 2003年论文《Practical Verifiable Encryption and Decryption of Discrete Logarithms》。

对应的代码实现在：https://github.com/KZen-networks/dlog-verifiable-enc

经验证，node版本用V10.20.1可以，用12版本存在兼容问题。 该代码用到了neon框架：Rust bindings for writing safe and fast native Node.js modules. 即内部是rust程序，外部是nodejs。

在该论文中主要关注的是proving properties about encrypted data. 在public-key encryption场景下，主要存在两方：

• 生成密文的一方；
• 拥有私有的一方。

协议也可分为：

• 若由加密方来提供证明，则称为verifiable encryption protocol；（本文主要关注verifiable encryption of discrete logarithm）
• 若由解密方来提供证明，则称为verifiable decryption protocol。（本文主要关注verifiable decryption of discrete logarithm）

具体描述如下图所示：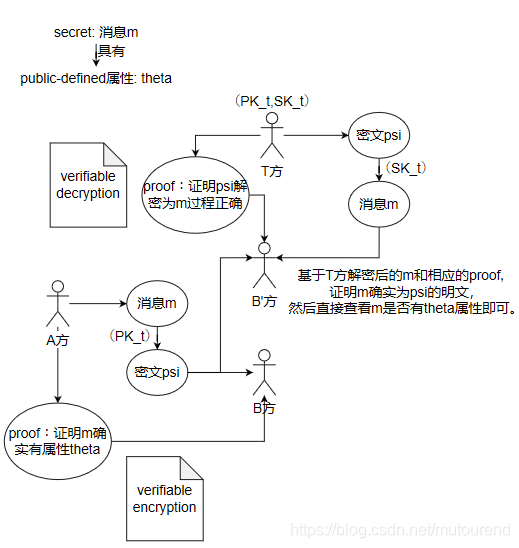

本论文只关注discrete logarithm属性：

• ψ = E n c p k ( m ) \psi=Enc_{pk}(m) ψ=Encpk​(m)，且 m m m具有 δ = γ m \delta=\gamma^m δ=γm属性，其中 ψ , P K , δ , γ \psi,PK,\delta,\gamma ψ,PK,δ,γ 对A方和B方均已知（为common input）；
• ψ = E n c p k ( m 1 , m 2 , ⋯   , m k ) \psi=Enc_{pk}(m_1,m_2,\cdots,m_k) ψ=Encpk​(m1​,m2​,⋯,mk​)，且 ( m 1 , m 2 , ⋯   , m k ) (m_1,m_2,\cdots,m_k) (m1​,m2​,⋯,mk​)具有 δ = γ 1 m 1 γ 2 m 2 ⋯ γ k m k \delta=\gamma_1^{m_1}\gamma_2^{m_2}\cdots\gamma_k^{m_k} δ=γ1m1​​γ2m2​​⋯γkmk​​属性，其中 ψ , P K , δ , ( γ 1 , γ 2 , ⋯   , γ k ) \psi,PK,\delta,(\gamma_1,\gamma_2,\cdots,\gamma_k) ψ,PK,δ,(γ1​,γ2​,⋯,γk​) 对A方和B方均已知（为common input）。

以上两类discrete logarithm属性在 key escrow秘钥托管，optimistic fair exchange乐观公平交互，publicly verifiable secret and signature sharing可公开验证的密码和签名共享，universally composable commitments通用组合承诺，group signatures群签名，和confirmer signatures确认人签名 等密码学应用场景中均非常有用。

• 本文的encryption scheme在Cramer and Shoup public key encryption scheme的基础上做了改进，可抵抗chosen ciphertext attack选择密文攻击；
• 本文的proof protocol，采用的是常用的three move “ Σ \Sigma Σ-protocol”。
• 本文的decryption过程除了verifiable decryption protocol外，也可以用threshold decryption protocol来实现，这样可以减少对decryptor的信任依赖。

1.1 verifiable encryption protocol

本文的verifiable encryption protocol 主要基于以下关键技术：

• Fujisaki and Okamoto’s method for proving relations on committed values [FO97] (with some refinements, as in [CS00, DF02])；
• the related interval proofs [CM98, CFT98]；
• Paillier encryption [Pai99]；
• Cramer and Shoup’s universal hash proof encryption technique [CS02]。

1.2 verifiable decryption protocol

本文的verifiable decryption protocol主要基于以下关键技术：

• Cramer, Damg˚ard, and Schoenmakers’ proofs of partial knowledge [CDS94]；
• Boudot’s exact interval proofs [Bou00]；
• new protocols for proving the inequality of discrete logarithms。

1.3 一些定义

a , b , c a,b,c a,b,c为整数，且 b > 0 b>0 b>0。

• non-negative remainder c = a m o d    b c=a\mod b c=amodb，其中 c = a − ⌊ a / b ⌋ b c=a-\left \lfloor a/b \right \rfloor b c=a−⌊a/b⌋b，所以有 0 ≤ c < b 0\leq c