隐私交易基本原则

1. 引言

ZCash, Monero, 以及所有基于CryptoNote的coins，都支持confidential transactions 隐私交易。

1.1 Bitcoin transaction

Bitcoin transaction的结构为： ( { a i } , { b i } , { v i } ) (\{a_i\},\{b_i\},\{v_i\}) ({ai},{bi},{vi})，其中 { a i } \{a_i\} {ai}为input addresses， { b i } \{b_i\} {bi}为output addresses， { v i } \{v_i\} {vi}为the amounts that go to each output。

在Bitcoin中，each transaction appears unencrypted for the whole world to see in the public ledger，使得比特币中的交易容易被跟踪，even when the coins go through multiple owners。解决交易跟踪问题的方式可为：

• 使用tumbler：takes in Bitcoin from many sources, mixes them around, and hands back some fresh uncorrelated coins。（类似于money laundering）
• confidential transaction：仅允许交易的参与方看见 v i v_i vi values，而对于其他非参与方均隐藏不可见。同时要求非参与方能够发现伪造的交易的。（don’t want a user to be able to print money by spending more than they actually have.）对于非参与方，account contents和output values都是保密的secret，怎么来验证交易是有效的呢？ ⇒ \Rightarrow ⇒ 需要用到的技术主要有： ** Schnorr Signature。 ** AOS Ring Signature。 ** Borromean Ring Signatures。 ** Pedersen Commitments。 ** Hiding Transaction Amounts。 ** Rangeproofs。

2. Schnorr Signature

详细可参见博客 ECDSA VS Schnorr signature VS BLS signature 第2节内容。

主要内容为：

• an abelian group G \mathbb{G} G of prime order q q q with generator G G G.
• public key P = x G P=xG P=xG, where x ∈ Z q x\in\mathbb{Z}_q x∈Zq is secret key。
• hash function H : { 0 , 1 } ∗ → Z q H:\{0,1\}^*\rightarrow \mathbb{Z}_q H:{0,1}∗→Zq.
• message to be signed M ∈ { 0 , 1 } ∗ M\in\{0,1\}^* M∈{0,1}∗

Schnorr 签名过程为：

• 选择随机数 a ← Z q a\leftarrow \mathbb{Z}_q a←Zq，设置 Q = a G Q=aG Q=aG;
• 计算 e = H ( Q ∣ ∣ M ) e=H(Q||M) e=H(Q∣∣M)
• 计算 s = a − e x s=a-ex s=a−ex
• 发送Schnorr signature σ = ( s , e ) \sigma=(s,e) σ=(s,e)

Schnorr验签过程为：

• 计算 Q = s G + e P Q=sG+eP Q=sG+eP
• 验证 e = H ( Q ∣ ∣ M ) e=H(Q||M) e=H(Q∣∣M)是否成立。

3. AOS Ring Signatures

confindential transactions底层使用的签名机制为ring signatures。ring signature 与普通签名类似，除了： a ring signature of the message m m m over the public keys { P 1 , P 2 , ⋯ , P n } \{P_1,P_2,\cdots,P_n\} {P1,P2,⋯,Pn} proves that someone with knowledge of one of the private keys { x 1 , x 2 , ⋯ , x n } \{x_1,x_2,\cdots,x_n\} {x1,x2,⋯,xn} has seen the message m m m。 普通签名为ring signature n = 1 n=1 n=1的特例。

ring signature的主要目的是： 隐藏实际进行签名的private key，具有signer ambiguity特性。（not reveal which private key it was that performed the signature.）

Abe,Okhubo,Suzuki 2002年论文《1-out-of-n Signatures from a Variety of Keys》中所构建的ring signature是Schnorr Signautre的generalization。

3.1 AOS Ring Signatures签名过程

假设 n n n 个 public keys { P 0 , P 1 , P 2 , ⋯ , P n − 1 } \{P_0,P_1,P_2,\cdots,P_{n-1}\} {P0,P1,P2,⋯,Pn−1} 中，签名方实际仅知道 P j P_j Pj的私钥 x j x_j xj，即该签名方实际仅能用 x j x_j xj对消息 M ∈ { 0 , 1 } ∗ M\in\{0,1\}^* M∈{0,1}∗进行签名。具体的AOS签名流程为：【注意下面的 j + 1 , i + 1 j+1,i+1 j+1,i+1等计算均做modulus n n n运算，保证实际下标不超过 n n n。】

• 随机数 a ← Z q a\leftarrow\mathbb{Z}_q a←Zq，计算 Q = a G , e j + 1 = H ( Q ∣ ∣ M ) Q=aG,e_{j+1}=H(Q||M) Q=aG,ej+1=H(Q∣∣M)；
• i i i的取值从 ( j + 1 m o d n ) (j+1\mod n) (j+1modn)开始， f o r ( i = ( j + 1 m o d n ) ; 0 ≤ i < n , i ≠ j ; i + + ) for\ (i=(j+1\mod n);0\leq i< n,i\neq j;i++) for (i=(j+1modn);0≤i<n,i=j;i++)，依次选择随机数 s i ← Z q s_i\leftarrow\mathbb{Z}_q si←Zq，依次计算 e i + 1 = H ( s i G + e i P i ∣ ∣ M ) e_{i+1}=H(s_iG+e_iP_i||M) ei+1=H(siG+eiPi∣∣M)。
• 设置 s j = a − e j x j s_j=a-e_jx_j sj=a−ejxj。
• 最终的AOS signature为 σ = ( e 0 , s 0 , s 1 , ⋯ , s n − 1 ) \sigma=(e_0,s_0,s_1,\cdots, s_{n-1}) σ=(e0,s0,s1,⋯,sn−1)。

举例： 已知 n = 3 n=3 n=3个 public keys { P 0 , P 1 , P 2 } \{P_0,P_1,P_2\} {P0,P1,P2}，签名者（我，I）的拥有的私钥为 x 1 x_1 x1满足 P 1 = x 1 G P_1=x_1G P1=x1G，进行AOS signature流程为：

• start making the ring at index 2: a ← Z q , e 2 = H ( a G ∣ ∣ M ) a\leftarrow \mathbb{Z}_q,e_2=H(aG||M) a←Zq,e2=H(aG∣∣M)；
• continue making the ring: s 2 ← Z q , e 0 = H ( s 2 G + e 2 P 2 ∣ ∣ M ) s_2\leftarrow \mathbb{Z}_q,e_0=H(s_2G+e_2P_2||M) s2←Zq,e0=H(s2G+e2P2∣∣M)；
• continue making the ring: s 0 ← Z q , e 1 = H ( s 0 G + e 0 P 0 ∣ ∣ M ) s_0\leftarrow \mathbb{Z}_q,e_1=H(s_0G+e_0P_0||M) s0←Zq,e1=H(s0G+e0P0∣∣M)；
• Now notice that e 2 e_2 e2 has been determined in two ways: from before, e 2 = H ( α G ∣ ∣ M ) e_2=H(αG||M) e2=H(αG∣∣M), and also from the property which must hold for every e e e value: e 2 = H ( s 1 G + e 1 P 1 ∣ ∣ M ) e_2=H(s_1G+e_1P_1||M) e2=H(s1G+e1P1∣∣M). The only s 1 s_1 s1 that satisfies these constraints is s 1 = α − e 1 x 1 s_1=α−e_1x_1 s1=α−e1x1, which I can easily compute, since I know x 1 x_1 x1.
• 最终的AOS ring signature为： σ = ( e 0 , s 0 , s 1 , s 2 ) \sigma=(e_0,s_0,s_1,s_2) σ=(e0,s0,s1,s2)。

3.2 AOS Ring Signatures验签过程

对AOS ring signature σ = ( e 0 , s 0 , s 1 , s 2 ) \sigma=(e_0,s_0,s_1,s_2) σ=(e0,s0,s1,s2)的验签过程为：

• 计算 e 1 = H ( s 0 G + e 0 P 0 ∣ ∣ M ) e_1=H(s_0G+e_0P_0||M) e1=H(s0G+e0P0∣∣M)；
• 计算 e 2 = H ( s 1 G + e 1 P 1 ∣ ∣ M ) e_2=H(s_1G+e_1P_1||M) e2=H(s1G+e1P1∣∣M)；
• 计算 e 0 = H ( s 2 G + e 2 P 2 ∣ ∣ M ) e_0=H(s_2G+e_2P_2||M) e0=H(s2G+e2P2∣∣M)；
• 验证 e 0 = e 0 e_0=e_0 e0=e0是否成立。

验签者无法知道哪个 s i s_i si值是真正的随机值，从而实现混淆签名者的作用。 【其实即为博客 基于Sigma protocol实现的零知识证明protocol集锦中2.3节的OR证明，或者博客 Proof Systems for General Statements about Discrete Logarithms 学习笔记中2.3和3节中的generalized OR证明】

实际实现时，在签名和验签过程中，没必要在计算每个 e i e_i ei时都hash M M M，可以调整为： e 0 = H ( s n − 1 G + e n − 1 P n − 1 ∣ M ) e_0=H(s_{n-1}G+e_{n-1}P_{n-1}|M) e0=H(sn−1G+en−1Pn−1∣M)，而每个除 e 0 e_0 e0之外的 e i + 1 = H ( s i G + e i P i ) e_{i+1}=H(s_iG+e_iP_i) ei+1=H(siG+eiPi)。

4. Borromean Ring Signatures

针对的场景为： 有multiple sets of public keys A ⃗ 1 , A ⃗ 2 , A ⃗ 3 \vec{A}_1,\vec{A}_2,\vec{A}_3 A 1,A 2,A 3，签名者（我，I）拥有one private key in each A ⃗ i \vec{A}_i A i，然后需要sign a message M M M in each of these rings. In doing so, I am proving "Some key in A ⃗ 1 \vec{A}_1 A 1 signed M M M AND Some key in A ⃗ 2 \vec{A}_2 A 2 signed M M M AND Some key in A ⃗ 3 \vec{A}_3 A 3 signed M M M"。

最直观的实现方式是： make a separate AOS signature for each set of public keys, giving us a final signature of σ = ( σ 1 , σ 2 , σ 3 ) \sigma=(\sigma_1,\sigma_2,\sigma_3) σ=(σ1,σ2,σ3)。 但是以上方式的签名长度过长，Gregory Maxwell，Andrew Poelstra 2015年论文《Borromean Ring Signatures》对此做了优化：

• pinning e 0 e_0 e0 as a shared e e e value for all rings A ⃗ i \vec{A}_i A i，该论文中 e 0 = H ( R 0 ∣ ∣ R 1 ∣ ∣ ⋯ ∣ ∣ R n − 1 ∣ ∣ M ) e_0=H(R_0||R_1||\cdots ||R_{n-1}||M) e0=H(R0∣∣R1∣∣⋯∣∣Rn−1∣∣M)，其中 R i = s i , m i − 1 G + e i , m i − 1 P i , m i − 1 R_i=s_{i,m_i-1}G+e_{i,m_i-1}P_{i,m_i-1} Ri=si,mi−1G+ei,mi−1Pi,mi−1 when j i ≠ m i − 1 j_i\neq m_i-1 ji=mi−1, and R i = a i G R_i=a_iG Ri=aiG otherwise。 m i m_i mi表示第 i i i个ring的public key数量， j i j_i ji表示在第 i i i个ring中所知道的private key的序号。 该算法的要点为：每个ring 的 the last e e e和 s s s值（其实对应index为 m i − 1 m_i-1 mi−1，无论是否对应为the known private key）都包含在 e 0 e_0 e0值中。 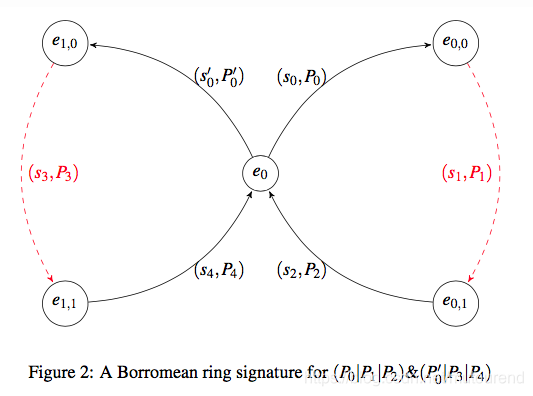最终的Borromean Ring Signatures为： σ = ( e 0 , ( s 0 , 0 , s 0 , 1 , ⋯ , s 1 , m 0 − 1 ) , ⋯ , ( s n − 1 , 0 , ⋯ , s n − 1 , m n − 1 − 1 ) ) \sigma=(e_0,(s_{0,0},s_{0,1},\cdots,s_{1,m_0-1}),\cdots,(s_{n-1,0},\cdots,s_{n-1,m_{n-1}-1})) σ=(e0,(s0,0,s0,1,⋯,s1,m0−1),⋯,(sn−1,0,⋯,sn−1,mn−1−1))

Borreomean ring signature的总长度为 ∑ m i + 1 \sum_{}m_i+1 ∑mi+1，相比于separate AOS signature for each set of public keys方案，可以节约 n − 1 n-1 n−1个数值。

5. Pedersen Commitments

A commitment is a value that is published prior to the revealing of some information. The commitment proves that you knew that information before it was revealed.

Pedersen commitment具有Hash函数所不具有的一些特性。

Pedersen commitment 要素有：

• an abelian group G \mathbb{G} G of prime order q q q;
• two public and unrelated generators G G G and H H H。（即无法找到 a a a，使得 a G = H aG=H aG=H成立。）

commit to value v ∈ Z q v\in\mathbb{Z}_q v∈Zq的流程为：

• 选择随机blinding factor α ← Z q \alpha\leftarrow\mathbb{Z}_q α←Zq；
• 计算 Q = α G + v H Q=\alpha G+vH Q=αG+vH。

若存在不同的 ( α ′ , v ′ ) (\alpha',v') (α′,v′)使得其commitment也为 Q Q Q，则有： α G + v H = α ′ G + v ′ H ⇒ ( α − α ′ ) G = ( v ′ − v ) H ⇒ G = v ′ − v α − α ′ H \alpha G+vH=\alpha' G+v'H\Rightarrow (\alpha-\alpha')G=(v'-v)H \Rightarrow G=\frac{v'-v}{\alpha-\alpha'}H αG+vH=α′G+v′H⇒(α−α′)G=(v′−v)H⇒G=α−α′v′−vH，违背了之前的 G G G和 H H H unrelated假设。

Pedersen commitment具有binding和hiding属性。同时具有加法同态属性： Q + Q ′ = C o m ( v ; α ) + C o m ( v ′ ; α ′ ) = C o m ( v + v ′ ; α + α ′ ) Q+Q'=Com(v;\alpha)+Com(v';\alpha')=Com(v+v';\alpha+\alpha') Q+Q′=Com(v;α)+Com(v′;α′)=Com(v+v′;α+α′)

6. Hiding Transaction Amounts隐藏交易金额

交易内金额主要有：（都 ∈ Z q \in \mathbb{Z}_q ∈Zq）

• input amount a a a；
• output amount b b b；
• transaction fee f f f。

交易内金额要满足公式 a = b + f a=b+f a=b+f，total input equals total output, so no money appears out of thin air and no money disappears into nothingess. 该公式可借助Pedersen commitment来实现 without revealing any of the values：

• 选择随机数 α a ← Z q , α b ← Z q \alpha_a\leftarrow\mathbb{Z}_q,\alpha_b\leftarrow\mathbb{Z}_q αa←Zq,αb←Zq，计算 α f = α a − α b \alpha_f=\alpha_a-\alpha_b αf=αa−αb；
• 计算Pedersen commitments P = α a G + a H , Q = α b G + b H , R = α f G + f H P=\alpha_a G+aH,Q=\alpha_b G+bH,R=\alpha_f G+fH P=αaG+aH,Q=αbG+bH,R=αfG+fH。在交易中发送 ( P , Q , R ) (P,Q,R) (P,Q,R)。
• 注意，仅仅验证 P − Q − R = ( α a − α b − α f ) G + ( a − b − f ) H = 0 G + 0 H = O P-Q-R=(\alpha_a -\alpha_b -\alpha_f)G+(a-b-f)H=0G+0H=\mathcal{O} P−Q−R=(αa−αb−αf)G+(a−b−f)H=0G+0H=O成立，只能证明 a − b − f ≡ 0 ( m o d q ) a-b-f\equiv 0(\mod q) a−b−f≡0(modq)成立，而不是 a − b − f = 0 a-b-f=0 a−b−f=0成立。 举例为：若 q = 13 q=13 q=13，input为1，output为9，transaction fee 5时， a − b − f = 1 − 9 − 5 = − 13 ≡ 0 ( m o d 13 ) a-b-f=1-9-5=-13\equiv 0(\mod 13) a−b−f=1−9−5=−13≡0(mod13)仍然成立， P − Q − R = O P-Q-R=\mathcal{O} P−Q−R=O验证也会通过。 但是存在溢出问题overflowed and ended up wrapping around the modulus。可借助Rangeproofs来解决。

7. Rangeproofs

为了overflowed and ended up wrapping around the modulus问题，且避免考虑负数情况，验证等式 a − b − f = 0 a-b-f=0 a−b−f=0成立改为验证 a = b + f a=b+f a=b+f成立。同时要求 b + f < q b+f