Boneh等人2018年论文《Compact Multi-Signatures for Smaller Blockchains》,论文解读参见博客 Compact Multi-Signatures for Smaller Blockchains学习笔记。 其中第5章为Discrete-Logarithm based multi-signature scheme MSDL,算法细节与Musig方案类似,详细可参见博客 Musig方案代码解析。【针对Schnorr signature。】
在本博客中主要解析的是https://github.com/lovesh/signature-schemes/bls仓库中基于pairing的multi-signature MSP/AMSP/ASM/PoP等算法实现。【针对BLS signature。】
看https://github.com/lovesh/signature-schemes/tree/master/bls/Cargo.toml中内容:
- https://github.com/lovesh/amcl_rust_wrapper:主要做了基础运算的constant time 和variable time function封装。支持的曲线主要有"bls381", “bn254”, “secp256k1”, “ed25519”。(具体可参见博客 Polynomial Commitments代码实现【2】——lovesh/kzg-poly-commit 第1节内容。)
[dependencies.amcl_wrapper]
version = "0.2.1"
default-features = false
features = ["bls381"]
- rand:随机数生成器,Musig方案中的随机数要求为strong random number。
- lazy_static:lazy_static是在第一次调用时(运行时)进行初始化。而非编译时,而static是在编译时进行初始化,运行阶段分配内存空间。(实际未使用,可去除。)
- log:提供日志接口。
- serde:A generic serialization/deserialization framework。
- serde_derive:Macros 1.1 implementation of #[derive(Serialize, Deserialize)]。
- secret_sharing:(https://github.com/lovesh/secret-sharing-schemes)主要用于辅助实现 threshold signatures,包含三组实现: –1)需要trusted third party的Shamir secret sharing; –2)不需要可信第三方的Pedersen verifiable secret sharing;【Torben P. Pedersen 1991年论文《Non-interactive and information-theoretic secure verifiable secret sharing》第4章。】 –3)不需要可信第三方的Pedersen decentralized verifiable secret sharing。Torben P. Pedersen 1991年论文《Non-interactive and information-theoretic secure verifiable secret sharing》第5章。】
Bilinear group通常为非对称的,其中的1个group具有a more compact(紧凑的) representation。 pairing-based MSP/AMSP均要求public key和signature在不同的groups(即live in different groups)。
- 对于标准签名来说,一个公钥会对很多消息签名,通常会选择用更紧凑的group来表示signatures。
["SignatureG2"] - 而在本论文中,由于需要同时支持signature aggregation和public key aggregation,则要根据实际应用来确定group选择。
[features]
default = ["SignatureG2"]
SignatureG1 = [] # signature and message are in G1, verification key in G2
SignatureG2 = [] # signature and message are in G2, verification key in G1
["SignatureG2"]:signature和message均在 G 2 G_2 G2,verification key 在 G 1 G_1 G1,对应的是验签很快,签名略慢。默认为["SignatureG2"]以保证验签速度。["SignatureG1"]:signature和message均在 G 1 G_1 G1,verification key 在 G 2 G_2 G2,对应的是签名很快,验签略慢。
总体代码结构为:
- lib.rs:引用的amcl_wrapper库针对不同group选择所对应的pairing函数接口调用。
- common.rs:签名key/验签key的结构体和初始化实现。
pub struct Keypair {
pub sig_key: SigKey, //私钥
pub ver_key: VerKey, //公钥
}
#[derive(Debug, Clone, Serialize, Deserialize, PartialEq)]
pub struct VerKey {
pub point: VerkeyGroup,
}
#[derive(Debug, Clone, Serialize, Deserialize, PartialEq)]
pub struct SigKey {
pub x: FieldElement,
}
- multi_sig_fast.rs:需要通过proof of possession (PoP) 来抵抗rogue key attack。【需要naive方案+PoP,实际test函数有待参考博客 Compact Multi-Signatures for Smaller Blockchains学习笔记中第4节内容进一步改进。】
- multi_sig_slow.rs:借助hash函数生成系数
a
i
a_i
ai,可抵抗rogue key attack。签名和验签速度都要比
multi_sig_fast.rs慢。对应为博客 Compact Multi-Signatures for Smaller Blockchains学习笔记中第2节内容。 - simple.rs:基础Signature
new/verify/batch_verify(不要求消息互不相同)和batch_verify_distinct_msgs(要求消息互不相同)算法实现。 - threshold_sig.rs:基于Accountable-Subgroup Multi-signatures (ASM)的门限签名实现。
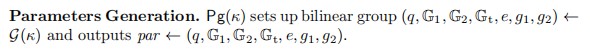
let params = Params::new("test".as_bytes());
pub struct Params {
pub g: VerkeyGroup,
}
impl Params {
pub fn new(label: &[u8]) -> Self {
// NUMS
let g = VerkeyGroup::from_msg_hash(label);
Params { g }
}
}

let mut rng = thread_rng();
let keypair = Keypair::new(&mut rng, ¶ms);
let sk = keypair.sig_key;
let vk = keypair.ver_key;
pub struct Keypair {
pub sig_key: SigKey,
pub ver_key: VerKey,
}
impl Keypair {
pub fn new(rng: &mut R, params: &Params) -> Self {
let sk = SigKey::new(rng);
let vk = VerKey::from_sigkey(&sk, params);
Keypair {
sig_key: sk,
ver_key: vk,
}
}
}
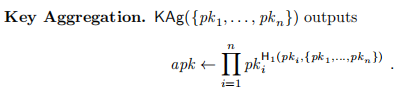
let mut sigs_and_ver_keys: Vec = Vec::new();
let mut avk = AggregatedVerKey::from_verkeys(&sigs_and_ver_keys);
sigs_and_ver_keys.push((sig, v));
// This is a newer but SLOWER way of doing BLS signature aggregation. This is NOT VULNERABLE to
// rogue public key attack so does not need proof of possession.
pub struct AggregatedVerKey {}
impl AggregatedVerKey {
/// Hashes a verkey with all other verkeys using a Hash function `H:{0, 1}* -> Z_q`
/// Takes a verkey `vk_i` and all verkeys `vk_1, vk_2,...vk_n` (including `vk_i`) and calculates
/// `H(vk_i||vk_1||vk_2...||vk_i||...vk_n)`
pub(crate) fn hashed_verkey_for_aggregation(
ver_key: &VerKey,
all_ver_key_bytes: impl IntoIterator,
) -> FieldElement {
// TODO: Sort the verkeys in some order to avoid accidentally passing wrong order of keys
let mut res_vec: Vec = Vec::new();
res_vec.extend_from_slice(&ver_key.to_bytes());
for vk_bytes in all_ver_key_bytes.into_iter() {
res_vec.extend_from_slice(vk_bytes.as_ref());
}
Self::hash_verkeys(res_vec.as_slice())
}
/// Calculates the aggregated verkey
/// For each `v_i` of the verkeys `vk_1, vk_2,...vk_n` calculate
/// `a_i = vk_i * hashed_verkey_for_aggregation(vk_i, [vk_1, vk_2,...vk_n])`
/// Add all `a_i`
pub fn from_verkeys(ver_keys: T) -> VerKey
where
T: IntoIterator,
T::IntoIter: Clone,
V: AsRef + 'a
{
let ver_keys = ver_keys.into_iter();
// TODO: Sort the verkeys in some order to avoid accidentally passing wrong order of keys
let vk_bytes: Vec = ver_keys.clone().map(|x| x.as_ref().to_bytes()).collect();
let (hs, vks): (Vec, Vec) = ver_keys
.map(|vk| (
AggregatedVerKey::hashed_verkey_for_aggregation(vk.as_ref(), &vk_bytes),
vk.as_ref().point.clone(),
))
.unzip();
let avk = VerkeyGroupVec::from(vks)
.multi_scalar_mul_var_time(&hs.into())
.unwrap();
VerKey { point: avk }
}
/// Hash verkey bytes to field element. H_1 from the paper.
pub(crate) fn hash_verkeys(verkey_bytes: &[u8]) -> FieldElement {
FieldElement::from_msg_hash(&[&VERKEY_DOMAIN_PREFIX, verkey_bytes].concat())
}
}

let mut asig = MultiSignature::from_sigs(&sigs_and_ver_keys);
/// The aggregator needs to know of all the signer before it can generate the aggregate signature.
/// Takes individual signatures from each of the signers and their verkey and aggregates the
/// signatures. For each signature `s_i` from signer with verkey `v_i` calculate
/// `a_i = hashed_verkey_for_aggregation(vk_i, [vk_1, vk_2,...vk_n])`
/// `a_si = s_i * a_i`
/// Add all `a_si`.
/// An alternate construction is (as described in the paper) to let signer compute `s_i * a_i` and
/// the aggregator simply adds each signer's output. In that model, signer does more work but in the
/// implemented model, aggregator does more work and the same signer implementation can be used by
/// signers of "slow" and "fast" implementation.
pub fn from_sigs(sigs_and_ver_keys: T) -> Signature
where
T: IntoIterator,
T::IntoIter: Clone,
I: AsRef + AsRef + 'a
{
let sigs_and_ver_keys = sigs_and_ver_keys.into_iter();
// TODO: Sort the verkeys in some order to avoid accidentally passing wrong order of keys
let all_ver_key_bytes: Vec = sigs_and_ver_keys
.clone()
.map(|x| AsRef::::as_ref(x).to_bytes())
.collect();
let (hs, sigs): (Vec, Vec) = sigs_and_ver_keys
.map(|x| (
AggregatedVerKey::hashed_verkey_for_aggregation(x.as_ref(), &all_ver_key_bytes),
AsRef::::as_ref(x).point.clone(),
))
.unzip();
let asig = SignatureGroupVec::from(sigs)
.multi_scalar_mul_var_time(&hs.into())
.unwrap();
Signature { point: asig }
}
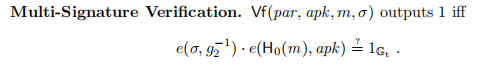
assert!(MultiSignature::verify(&asig, &b, &sigs_and_ver_keys, ¶ms));
或者
assert!(asig.verify(&b, &avk, ¶ms));
/// An aggregate VerKey is created from `ver_keys`. When verifying signature using the same
/// set of keys frequently generate a verkey once and then use `Signature::verify`
pub fn verify(sig: &Signature, msg: &[u8], ver_keys: T, params: &Params) -> bool
where
T: IntoIterator,
T::IntoIter: Clone,
K: AsRef + 'a
{
let avk = AggregatedVerKey::from_verkeys(ver_keys);
sig.verify(msg, &avk, params)
}
pub fn verify(&self, msg: &[u8], ver_key: &VerKey, params: &Params) -> bool {
// TODO: Check if point exists on curve, maybe use `ECP::new_big` and x cord of verkey
if self.point.is_identity() {
println!("Signature point at infinity");
return false;
}
let msg_hash_point = Self::hash_message(msg);
// e(self.point, params.g) == e(msg_hash_point, ver_key.point) =>
// e(msg_hash_point, ver_key.point) * e(self.point, params.g)^-1 == 1 =>
// e(msg_hash_point, ver_key.point) * e(self.point, params.g^-1) == 1
ate_2_pairing(
&msg_hash_point,
&ver_key.point,
&self.point,
¶ms.g.negation(),
)
.is_one()
}
 注意
注意batch_verifiy中用
(
r
,
r
2
,
⋯
,
r
b
)
(r,r^2,\cdots,r^b)
(r,r2,⋯,rb)(:new_vandermonde_vector函数)来代替
(
ρ
1
,
⋯
,
ρ
b
)
(\rho_1,\cdots,\rho_b)
(ρ1,⋯,ρb)。
/// Batch verification of signatures. Takes a vector of 3-tuple where each tuple has a message,
/// signature and public key. Messages can be same or different
pub fn batch_verify(msgs_sigs: Vec, params: &Params) -> bool {
let r = FieldElement::random();
let r_vec = FieldElementVector::new_vandermonde_vector(&r, msgs_sigs.len());
let mut sigs = SignatureGroupVec::with_capacity(msgs_sigs.len());
let mut hs = vec![];
let mut vs = vec![];
for (i, (msg, sig, vk)) in msgs_sigs.iter().enumerate() {
sigs.push(sig.point.clone());
hs.push(Signature::hash_message(msg));
// The multiplication with &r_vec[i] can be moved to message instead of verkey but
// since verkey is in group G1 by default and operations in G1 are cheaper.
// A better way would be to have code conditional on features such that
// multiplication is moved to message when messages are in G1 and verkey in G2.
vs.push(&vk.point * &r_vec[i]);
}
let aggr_sig = sigs.multi_scalar_mul_var_time(&r_vec).unwrap();
let mut pairings = hs
.iter()
.zip(vs.iter())
.map(|(h, v)| (h, v))
.collect::();
let neg_g = params.g.negation();
pairings.push((&aggr_sig, &neg_g));
ate_multi_pairing(pairings).is_one()
}
/// Batch verification of signatures. Takes a vector of 3-tuple where each tuple has a message,
/// signature and public key. Assumes all messages to be distinct
pub fn batch_verify_distinct_msgs(
msgs_sigs: Vec,
params: &Params,
) -> bool {
let mut aggr_sig = SignatureGroup::new();
let mut hs = vec![];
let mut vs = vec![];
for (msg, sig, vk) in msgs_sigs {
aggr_sig += &sig.point;
hs.push(Signature::hash_message(msg));
vs.push(vk);
}
let mut pairings = hs
.iter()
.zip(vs)
.map(|(h, v)| (h, &v.point))
.collect::();
let neg_g = params.g.negation();
pairings.push((&aggr_sig, &neg_g));
ate_multi_pairing(pairings).is_one()
}
即相当于用私钥对公钥进行签名。
#[test]
fn proof_of_possession() {
let mut rng = thread_rng();
let params = Params::new("test".as_bytes());
let keypair = Keypair::new(&mut rng, ¶ms);
let sk = keypair.sig_key;
let vk = keypair.ver_key;
let proof = ProofOfPossession::generate(&vk, &sk);
assert!(ProofOfPossession::verify(&proof, &vk, ¶ms));
}
pub struct ProofOfPossession {}
impl ProofOfPossession {
// Used for domain separation while creating Proof of Possession
const PoP_DOMAIN_PREFIX: [u8; 2] = [2, 2];
pub fn generate(verkey: &VerKey, sigkey: &SigKey) -> Signature {
Signature::new(
&[&Self::PoP_DOMAIN_PREFIX, verkey.to_bytes().as_slice()].concat(),
&sigkey,
)
}
pub fn verify(proof: &Signature, verkey: &VerKey, params: &Params) -> bool {
proof.verify(
&[&Self::PoP_DOMAIN_PREFIX, verkey.to_bytes().as_slice()].concat(),
verkey,
params,
)
}
}
其中的Parameter generation, key generation, and key aggregation 分别与3.1/3.2/3.3节的算法一致。不同之处在于, 在key generation之前需增加Group Setup算法 ,相应的Signing和Verification算法也有所不同。
let params = Params::new("test".as_bytes());
ASM的整个签名过程为非交互的。但是初始的key generation 需要在所有
n
n
n个签名者之间运行a simple one-round protocol,使得每个签名者都可obtain a group-specific membership key
m
k
mk
mk that it needs to sign messages for the group
P
K
\mathcal{PK}
PK。  ASM中所有签名者需要有统一全局的index,整个过程可由可信第三方执行Shamir secret sharing来构建,而不再使用论文中的hash函数
H
0
,
H
1
,
H
2
H_0,H_1,H_2
H0,H1,H2。(具体可参见博客 verifiable secret sharing可验证的秘密共享) 【借用的思想为:aggregate secret key对应为aggregate public key。以下
ASM中所有签名者需要有统一全局的index,整个过程可由可信第三方执行Shamir secret sharing来构建,而不再使用论文中的hash函数
H
0
,
H
1
,
H
2
H_0,H_1,H_2
H0,H1,H2。(具体可参见博客 verifiable secret sharing可验证的秘密共享) 【借用的思想为:aggregate secret key对应为aggregate public key。以下secret_x为有毒垃圾,应丢弃。threshold_vk即为aggregate public key。】 
pub struct Signer {
pub id: usize,
pub sigkey: SigKey,
pub verkey: VerKey,
}
let threshold = 3;
let total = 6;
let (secret_x, signers) = trusted_party_SSS_keygen(threshold, total, ¶ms);
let mut keys = vec![];
keys.push((signers[0].id, &signers[0].verkey));
keys.push((signers[2].id, &signers[2].verkey));
keys.push((signers[4].id, &signers[4].verkey));
check_threshold_key_gen_gaps_in_ids(threshold, secret_x, keys, ¶ms);//验证aggregate secret key对应为aggregate public key。
/// Keygen done by trusted party using Shamir secret sharing. Creates signing and verification
/// keys for each signer. The trusted party will know every signer's secret keys and the
/// aggregate secret keys and can create signatures.
/// Outputs 2 items, first is the shared secret and should be destroyed.
/// The second contains the keys, 1 item corresponding to each signer.
pub fn trusted_party_SSS_keygen(
threshold: usize,
total: usize,
params: &Params,
) -> (FieldElement, Vec) {
let (secret_x, x_shares) = get_shared_secret(threshold, total);
(secret_x, keygen_from_shares(total, x_shares, params))
}
/// Takes shares for x and generate signing and verification keys
fn keygen_from_shares(
num_signers: usize,
mut x_shares: HashMap,
params: &Params,
) -> Vec {
let mut signers = vec![];
for i in 0..num_signers {
let id = i + 1;
let x_i = x_shares.remove(&id).unwrap();
let g_x_i = ¶ms.g * &x_i;
signers.push(Signer {
id,
sigkey: SigKey { x: x_i },
verkey: VerKey { point: g_x_i },
})
}
signers
}
fn check_threshold_key_gen_gaps_in_ids(
threshold: usize,
secret_x: FieldElement,
keys_to_aggr: Vec,
params: &Params,
) {
let threshold_vk = ThresholdScheme::aggregate_vk(threshold, keys_to_aggr);
let expected_vk = ¶ms.g * &secret_x;
assert_eq!(expected_vk, threshold_vk.point);
}
pub fn aggregate_vk(threshold: usize, keys: Vec) -> VerKey {
assert!(keys.len() >= threshold);
let mut vk_bases = VerkeyGroupVec::with_capacity(threshold);
let mut vk_exps = FieldElementVector::with_capacity(threshold);
let signer_ids = keys
.iter()
.take(threshold)
.map(|(i, _)| *i)
.collect::();
for (id, vk) in keys.into_iter().take(threshold) {
let l = Polynomial::lagrange_basis_at_0(signer_ids.clone(), id);
vk_bases.push(vk.point.clone());
vk_exps.push(l.clone());
}
// threshold verkey = vk_1^l_1 * vk_2^l_2 * ... vk_i^l_i for i in threshold
VerKey {
point: vk_bases.multi_scalar_mul_var_time(&vk_exps).unwrap(),
}
}
/// Generate a random polynomial with the secret at the polynomial evaluation at 0.
pub fn get_shared_secret_with_polynomial(
threshold: usize,
total: usize,
) -> (FieldElement, HashMap, Polynomial) {
let random_poly = Polynomial::random(threshold - 1);
let secret = random_poly.eval(&FieldElement::zero());
let shares = (1..=total)
.map(|x| (x, random_poly.eval(&FieldElement::from(x as u64))))
.collect::();
(secret, shares, random_poly)
}
/// Generate a secret with its shares according to Shamir secret sharing.
/// Returns the secret and a map of share_id -> share
pub fn get_shared_secret(
threshold: usize,
total: usize,
) -> (FieldElement, HashMap) {
let (secret, shares, _) = get_shared_secret_with_polynomial(threshold, total);
(secret, shares)
}
/// Return the Lagrange basis polynomial at x = 0 given the x coordinates
pub fn lagrange_basis_at_0(x_coords: HashSet, i: usize) -> FieldElement {
let mut numerator = FieldElement::one();
let mut denominator = FieldElement::one();
let i_as_field_elem = FieldElement::from(i as u64);
let neg_i = -i_as_field_elem; // -i
for x in x_coords {
if x == i {
continue;
}
// numerator = numerator * x
let x_as_field_elem = FieldElement::from(x as u64);
numerator = &numerator * &x_as_field_elem;
let x_minus_i = &x_as_field_elem + &neg_i;
// denominator = denominator * (x - i)
denominator = &denominator * &x_minus_i;
}
denominator.inverse_mut();
// (x_coords[0]) * (x_coords[1]) * ... / ((x_coords[0] - i) * (x_coords[1] - i) * ...)
numerator * denominator
}
let mut keys = vec![];
keys.push((signers[1].id, &signers[1].verkey)); // signer id is 2
keys.push((signers[3].id, &signers[3].verkey)); // signer id is 4
keys.push((signers[5].id, &signers[5].verkey)); // signer id is 6
let threshold_vk = ThresholdScheme::aggregate_vk(threshold, keys);

// Signers from which signature will be requested.
let mut signer_ids = HashSet::new();
signer_ids.insert(1);
signer_ids.insert(3);
signer_ids.insert(5);
let mut sigs = vec![];
for i in &signer_ids {
let sig = Signature::new(&msg, &signers[*i].sigkey);
assert!(sig.verify(&msg, &signers[*i].verkey, ¶ms));
sigs.push((signers[*i].id, sig));
}
let threshold_sig = ThresholdScheme::aggregate_sigs(threshold, sigs);
pub fn aggregate_sigs(threshold: usize, sigs: Vec) -> Signature {
assert!(sigs.len() >= threshold);
let mut s_bases = SignatureGroupVec::with_capacity(threshold);
let mut s_exps = FieldElementVector::with_capacity(threshold);
let signer_ids = sigs
.iter()
.take(threshold)
.map(|(i, _)| *i)
.collect::();
for (id, sig) in sigs.into_iter().take(threshold) {
let l = Polynomial::lagrange_basis_at_0(signer_ids.clone(), id);
s_bases.push(sig.point.clone());
s_exps.push(l);
}
// theshold signature = sig[i]^l for all i
Signature {
point: s_bases.multi_scalar_mul_const_time(&s_exps).unwrap(),
}
}
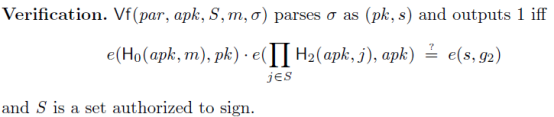
assert!(threshold_sig.verify(&msg, &threshold_vk, ¶ms));
可以像普通signature一样用aggregate public key进行直接验签。



