Practical Zero-Knowledge Protocols Based on the Discrete Logarithm Assumption 学习笔记 3

1. 引言

Stephanie Bayer 2013年博士论文 《Practical Zero-Knowledge Protocols Based on the Discrete Logarithm Assumption》。

要点：

• 1）各种non-membership argument的性能对比为：
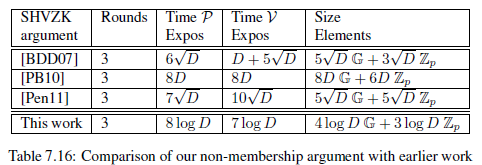
• 2）各种基于ElGamal encryption构建的shuffle argument性能对比为：

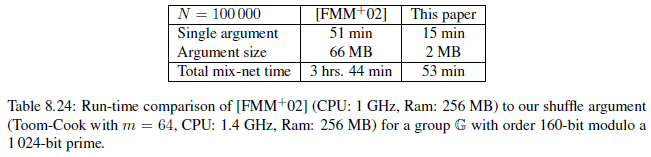
前序博客为：

• Practical Zero-Knowledge Protocols Based on the Discrete Logarithm Assumption 学习笔记 1，在该博客中主要关注论文前5章的内容。
• Practical Zero-Knowledge Protocols Based on the Discrete Logarithm Assumption 学习笔记 2，在该博客中主要关注论文第6章内容——polynomial evaluation argument （单变量、多变量以及batch）。

本博客主要关注论文第7章及之后内容——即主要关注相关应用，如membership/non-membership argument以及shuffle等。

2. non-membership/membership argument

non-membership argument to a public list 针对的是：

• public info：list L = { λ 1 , ⋯   , λ D } \mathcal{L}=\{\lambda_1,\cdots,\lambda_D\} L={λ1​,⋯,λD​} 和 commitment c u c_u cu​ 。
• private info： u u u。
• relation： u u u is not contained in L \mathcal{L} L。

membership argument 针对的是：

• public info：list L = { λ 1 , ⋯   , λ D } \mathcal{L}=\{\lambda_1,\cdots,\lambda_D\} L={λ1​,⋯,λD​} 和 commitment c u c_u cu​ 。
• private info： u u u。
• relation： u u u is contained in L \mathcal{L} L。

non-membership argument 的应用有：

• 可在用户不暴露IP等隐私信息的情况下，实现黑名单控制。
• 也可用于证明 a member of a group signature scheme is not revoked。（同时，depending on the setup of the group signature scheme, 用户可使用membership proof来证明其具有相应的签名权限。）

membership argument 的应用有：

• 实现白名单控制。
• 用于e-voting或e-auction中，证明其选票是有效的或证明其出价在指定的范围内。

本文基于polynomial evaluation argument 构建的 membership 和 non-membership argument 具有 logarithmic communication complexity。

核心思路为： 针对public list L = { λ 1 , ⋯   , λ D } \mathcal{L}=\{\lambda_1,\cdots,\lambda_D\} L={λ1​,⋯,λD​} 构建多项式： P ( X ) = ∏ i = 1 D ( X − λ i ) P(X)=\prod_{i=1}^{D}(X-\lambda_i) P(X)=∏i=1D​(X−λi​) 然后针对secret info u u u，计算 P ( u = v ) P(u=v) P(u=v) 并 commit to v v v 获得 c v c_v cv​。

对于non-membership u ∉ L u\notin \mathcal{L} u∈/​L，有 P ( u ) ≠ 0 P(u)\neq 0 P(u)​=0，即需证明 c v c_v cv​为非0值的commitment；对于membership u ∈ L u\in \mathcal{L} u∈L，有 P ( u ) = 0 P(u)=0 P(u)=0，即需证明 c v c_v cv​为0的commitment。

2.1 基于polynomial evaluation argument实现non-membership argument to a public list

对于non-membership u ∉ L u\notin \mathcal{L} u∈/​L，有 P ( u ) ≠ 0 P(u)\neq 0 P(u)​=0，即需证明 c v c_v cv​为非0值的commitment。 v ≠ 0 v\neq 0 v​=0，即意味这存在 v − 1 v^{-1} v−1，可直接调用博客 Practical Zero-Knowledge Protocols Based on the Discrete Logarithm Assumption 学习笔记 1 “5.2 Invertible argument” 即可。

完整的non-membership argument to a public list 证明为：

2.2 non-membership argument to a secret list

non-membership argument to a public list 针对的是：

• public info：commitments { c λ 1 , ⋯   , c λ D } \{c_{\lambda_1},\cdots,c_{\lambda_D}\} {cλ1​​,⋯,cλD​​} 和 commitment c u c_u cu​ 。
• private info： u u u 和 list L = { λ 1 , ⋯   , λ D } \mathcal{L}=\{\lambda_1,\cdots,\lambda_D\} L={λ1​,⋯,λD​}
• relation： u u u is not contained in L \mathcal{L} L。

构建多项式： P ( X ) = ∏ i = 1 D ( X − λ i ) = ∑ i = 0 D a i X i P(X)=\prod_{i=1}^{D}(X-\lambda_i)=\sum_{i=0}^{D}a_iX^i P(X)=∏i=1D​(X−λi​)=∑i=0D​ai​Xi

由于此处对应的是secret list（即Verifier不知道多项式的系数 a i a_i ai​），若使用polynomial evaluation argument，Verifier无法计算 δ ˉ = ∑ i 0 , ⋯   , i d = 0 1 a i 0 ⋯ i d ∏ j = 0 d f ˉ j i j x 1 − i j \bar{\delta}=\sum_{i_0,\cdots,i_d=0}^{1}a_{i_0\cdots i_d}\prod_{j=0}^{d}\bar{f}_j^{i_j}x^{1-i_j} δˉ=∑i0​,⋯,id​=01​ai0​⋯id​​∏j=0d​fˉ​jij​​x1−ij​ 。

by padding with zero-coefficients，可without loss of generality的假设 D = 2 d + 1 − 1 D=2^{d+1}-1 D=2d+1−1，将 i i i以二进制表示为 i = i 0 ⋯ i d i=i_0\cdots i_d i=i0​⋯id​，其中 i j ∈ { 0 , 1 } i_j\in\{0,1\} ij​∈{0,1}，可将 X i X^i Xi表示为： X i = X ∑ j = 0 d i j 2 j = ∏ j = 0 d ( X 2 j ) i j X^i=X^{\sum_{j=0}^{d}i_j2^j}=\prod_{j=0}^{d}(X^{2^j})^{i_j} Xi=X∑j=0d​ij​2j=∏j=0d​(X2j)ij​

替换进多项式中有：【因此此处可用博客 Practical Zero-Knowledge Protocols Based on the Discrete Logarithm Assumption 学习笔记 1 “5.3.4 single value product argument for secret b b b” 来进行证明】 P ( X ) = ∑ i = 0 D a i X i = ∑ i 0 , ⋯   , i d = 0 1 a i 0 ⋯ i d ∏ j = 0 d ( X 2 j ) i j P(X)=\sum_{i=0}^{D}a_iX^i=\sum_{i_0,\cdots,i_d=0}^{1}a_{i_0\cdots i_d}\prod_{j=0}^{d}(X^{2^j})^{i_j} P(X)=∑i=0D​ai​Xi=∑i0​,⋯,id​=01​ai0​⋯id​​∏j=0d​(X2j)ij​

基本的证明思路为：【 d = ⌊ log ⁡ D ⌋ d=\left \lfloor \log D \right \rfloor d=⌊logD⌋】

• Prover： 1）需单独对多项式系数进行commit，生成commitments c a 0 , c a 1 , ⋯   , c a D c_{a_0},c_{a_1},\cdots,c_{a_D} ca0​​,ca1​​,⋯,caD​​。 2）计算 v = P ( u ) v=P(u) v=P(u)。 3）计算commitment c v = C o m c k ( v ; s ) c_v=Com_{ck}(v;s) cv​=Comck​(v;s)，其中 s ← Z q s\leftarrow \mathbb{Z}_q s←Zq​。 4）计算commitments c u 1 = C o m c k ( u 2 1 ; r 1 ) , ⋯   , c u d = C o m c k ( u 2 d ; r d ) c_{u_1}=Com_{ck}(u^{2^1};r_1),\cdots,c_{u_d}=Com_{ck}(u^{2^d};r_d) cu1​​=Comck​(u21;r1​),⋯,cud​​=Comck​(u2d;rd​)，其中 r 1 , ⋯   , r d ← Z q r_1,\cdots,r_d\leftarrow \mathbb{Z}_q r1​,⋯,rd​←Zq​。 5）选择随机数 f 0 , s 0 , ⋯   , f d , s d ← Z q f_0,s_0,\cdots,f_d,s_d\leftarrow \mathbb{Z}_q f0​,s0​,⋯,fd​,sd​←Zq​，计算commitments c f 0 = C o m c k ( f 0 ; s 0 ) , ⋯   , c f d = C o m c k ( f d ; s d ) c_{f_0}=Com_{ck}(f_0;s_0),\cdots,c_{f_d}=Com_{ck}(f_d;s_d) cf0​​=Comck​(f0​;s0​),⋯,cfd​​=Comck​(fd​;sd​)。 6）计算 δ 0 , ⋯   , δ d ∈ Z q \delta_0,\cdots,\delta_d\in\mathbb{Z}_q δ0​,⋯,δd​∈Zq​，使得： ∑ i 0 , ⋯   , i d = 0 1 a i 0 ⋯ i d ∏ j = 0 d ( X u 2 j + f j ) i j X 1 − i j = X d + 1 v + ∑ j = 0 d X j δ j \sum_{i_0,\cdots,i_d=0}^{1}a_{i_0\cdots i_d}\prod_{j=0}^{d}(Xu^{2^j}+f_j)^{i_j}X^{1-i_j}=X^{d+1}v+\sum_{j=0}^{d}X^j\delta_j ∑i0​,⋯,id​=01​ai0​⋯id​​∏j=0d​(Xu2j+fj​)ij​X1−ij​=Xd+1v+∑j=0d​Xjδj​ 7）计算commitments c δ 0 = C o m c k ( δ 0 ; t 0 ) , ⋯   , c δ d = C o m c k ( δ d ; t d ) c_{\delta_0}=Com_{ck}(\delta_0;t_0),\cdots,c_{\delta_d}=Com_{ck}(\delta_d;t_d) cδ0​​=Comck​(δ0​;t0​),⋯,cδd​​=Comck​(δd​;td​)，其中 t 0 , ⋯   , t d ← Z q t_0,\cdots,t_d\leftarrow \mathbb{Z}_q t0​,⋯,td​←Zq​。 8）计算commitments c f u 0 = C o m c k ( f 0 u 2 0 ; ξ 0 ) , ⋯   , c f u d − 1 = C o m c k ( f d − 1 u 2 d − 1 ; ξ d − 1 ) c_{fu_0}=Com_{ck}(f_0u^{2^0};\xi_0),\cdots,c_{fu_{d-1}}=Com_{ck}(f_{d-1}u^{2^{d-1}};\xi_{d-1}) cfu0​​=Comck​(f0​u20;ξ0​),⋯,cfud−1​​=Comck​(fd−1​u2d−1;ξd−1​)，其中 ξ 0 , ⋯   , ξ d − 1 ← Z q \xi_0,\cdots,\xi_{d-1}\leftarrow \mathbb{Z}_q ξ0​,⋯,ξd−1​←Zq​。 Prover将 c a 0 , c a 1 , ⋯   , c a D c_{a_0},c_{a_1},\cdots,c_{a_D} ca0​​,ca1​​,⋯,caD​​， c v c_v cv​， c f 0 , ⋯   , c f d c_{f_0},\cdots,c_{f_d} cf0​​,⋯,cfd​​， c δ 0 , ⋯   , c δ d c_{\delta_0},\cdots,c_{\delta_d} cδ0​​,⋯,cδd​​， c f u 0 , ⋯   , c f u d − 1 c_{fu_0},\cdots,c_{fu_{d-1}} cfu0​​,⋯,cfud−1​​ 发送给Verifier。

• Verifier：发送challenge x ← Z q ∗ x\leftarrow \mathbb{Z}_q^* x←Zq∗​。

• Prover：

• Verifier： 整个non-membership argument to a secret list 算法的运行效率分析为：

2.3 membership argument

将2.1中的inverse argument替换为zero argument 即可。

Zero argument为标准的 and only cost a couple of group elements in communication [Sch91] （Schnorr 1991年论文《 Efficient signature generation by smart cards》），具体也可参见博客 基于Sigma protocol实现的零知识证明protocol集锦 “2.13 commitment to 0”。

2.4 multi non-membership/membership argument

考虑的场景为： 有many committed values u 1 , ⋯   , u L u_1,\cdots,u_L u1​,⋯,uL​ 和 blacklists L 1 , ⋯   , L L \mathcal{L}_1,\cdots,\mathcal{L}_L L1​,⋯,LL​，可构建多个不同的poynomials： v 1 = P ( 1 ) ( u 1 ) , ⋯   , v L = P ( L ) ( u L ) v_1=P^{(1)}(u_1),\cdots,v_L=P^{(L)}(u_{L}) v1​=P(1)(u1​),⋯,vL​=P(L)(uL​)。

• 对于multi non-membership argument，有 v 1 ≠ 0 , ⋯   , v L ≠ 0 v_1\neq 0,\cdots,v_L\neq 0 v1​​=0,⋯,vL​​=0，即可通过invertible argument和batch polynomial evaluation argument来实现。相应的communication complexity为 O ( L log ⁡ D ) O(\sqrt{L}\log D) O(L ​logD) group and field elements。
• 对于multi membership argument，有 v 1 = 0 , ⋯   , v L = 0 v_1=0,\cdots,v_L=0 v1​=0,⋯,vL​=0，可通过 multiple polynomial evaluation argument 和 Groth 2009年论文《Linear algebra with sub-linear zero-knowledge arguments》中的标准技术来实现。
• 对于白名单和黑名单混合的情况，仍然可以用polynomial evaluation argument来证明 v 1 = P ( 1 ) ( u 1 ) , ⋯   , v L = P ( L ) ( u L ) v_1=P^{(1)}(u_1),\cdots,v_L=P^{(L)}(u_L) v1​=P(1)(u1​),⋯,vL​=P(L)(uL​)，同时利用invertible argument来证明黑名单中的 v i ≠ 0 v_i\neq 0 vi​​=0，用zero argument来证明白名单中的 v i = 0 v_i=0 vi​=0。相应的communication complexity也为 O ( L log ⁡ D ) O(\sqrt{L}\log D) O(L ​logD)。

2.5 Brands [BDD07]中的non-membership argument

Brands [BDD07] 2007年论文《A practical system for globally revoking the unlinkable pseudonyms of unknown users》中，构建了a non-membership argument for u ∈ Z q u\in\mathbb{Z}_q u∈Zq​ and a list L = { λ 1 , ⋯   , λ D } \mathcal{L}=\{\lambda_1,\cdots,\lambda_D\} L={λ1​,⋯,λD​}，具有的communication cost为 O ( D ) O(\sqrt{D}) O(D ​)。

核心思路为： 详细的证明思路为：

3. zero-knowledge shuffle argument

相应的研究成果已发表在Bayer和Groth 2012年论文《Efficient zero-knowledge argument for correctness of a shuffle》。 也可参看系列博客：

• 1）Efficient Zero-Knowledge Argument for Correctness of a Shuffle学习笔记（1）
• 2）Efficient Zero-Knowledge Argument for Correctness of a Shuffle学习笔记（2）
• 3）Efficient Zero-Knowledge Argument for Correctness of a Shuffle学习笔记（3）

Chaum 1981年论文《Untraceable electronic mail, return addresses, and digital pseudonyms》中提出的mix-net可用于构建e-voting scheme。mix-net为 a multi-party protocol，允许a group of senders to input a number of encrypted messages to the mix-net, which then outputs them in random order。mix-net可用于需要匿名的场景，如anonymous broadcast。

可利用shuffle来构建mix-net，shuffle也可用于onion-routing和oblivious databases。

Shuffle是指： a shuffle of ciphertexts C 1 , ⋯   , C N C_1,\cdots,C_N C1​,⋯,CN​ is a set of ciphertexts C 1 ′ , ⋯   , C N ′ C_1',\cdots,C_N' C1′​,⋯,CN′​ with the same plaintexts in permuted order。

本文基于homomorphic encryption scheme构建了a shuffle protocol，即： a given public key p k pk pk, messages M 1 , M 2 M_1,M_2 M1​,M2​ and randomness ρ 1 , ρ 2 \rho_1,\rho_2 ρ1​,ρ2​，相应的entryption function 满足 ε p k ( M 1 M 2 ; ρ 1 + ρ 2 ) = ε p k ( M 1 ; ρ 1 ) ε p k ( M 2 ; ρ 2 ) \varepsilon_{pk}(M_1M_2;\rho_1+\rho_2)=\varepsilon_{pk}(M_1;\rho_1)\varepsilon_{pk}(M_2;\rho_2) εpk​(M1​M2​;ρ1​+ρ2​)=εpk​(M1​;ρ1​)εpk​(M2​;ρ2​)。【具有乘法同态属性。】 然后构建 a shuffle of C 1 , ⋯   , C N C_1,\cdots,C_N C1​,⋯,CN​ by selecting a permutation π ∈ ∑ N \pi\in\sum_N π∈∑N​ and randomizers ρ 1 , ⋯   , ρ N \rho_1,\cdots,\rho_N ρ1​,⋯,ρN​，计算 C 1 ′ = C π ( 1 ) ε p k ( 1 ; ρ 1 ) , ⋯   , C N ′ = C π ( N ) ε p k ( 1 ; ρ N ) C_1'=C_{\pi(1)}\varepsilon_{pk}(1;\rho_1),\cdots,C_N'=C_{\pi(N)}\varepsilon_{pk}(1;\rho_N) C1′​=Cπ(1)​εpk​(1;ρ1​),⋯,CN′​=Cπ(N)​εpk​(1;ρN​)。

构建mix-net的方式可为： 由mix-servers一次shuffle the ciphertexts，若所选择的encryption scheme为IND-CPA secure （选择明文攻击下的不可区分性 Indistinguishability under chosen-plaintext attack），即由一个mix-server输出的shuffle C 1 ′ , ⋯   , C N ′ C_1',\cdots,C_N' C1′​,⋯,CN′​ 既不会泄露the permutation，也不会泄露 the messages。 但是，这意味着在该mix-net 中可存在a milicous mix-server，可替换某些ciphertexts而不被发现。在voting protocol中，即以为着可替换all ciphertexts with encrypted votes for candidate X X X。 因此需要构建a zero-knowledge shuffle argument，满足：

• 证明the shuffle was done correctly (soundness)。
• reveal nothing about the permutation or the randomizers used (zero-knowledge)。

本文针对的encryption scheme为ElGamal encryption scheme，也可调整为其它homomorphic encryption scheme。

当shuffl N N N ciphertexts时，布局为an m × n m\times n m×n matrix：

• Groth和Ishai 2008年论文[GI08]《Sub-linear zero-knowledge argument for correctness of a shuffle》中构建的shuffle argument，需发送 Ω ( m 2 + n ) \Omega(m^2+n) Ω(m2+n) group elements。 且[GI08] 论文中的一个主要缺陷为： Prover的computational complexity为 O ( N m ) O(Nm) O(Nm) exponentiations，所以需选择small m m m。

• 本文构建的shuffle argument仅需发送 O ( m + n ) O(m+n) O(m+n) group elements，具有最小的communication complexity O ( N ) O(\sqrt{N}) O(N ​)。 本文的Prover computational complexity为 O ( N log ⁡ m ) O(N\log m) O(Nlogm) exponentiations for constant round arguments，或者是 O ( N ) O(N) O(N) exponentiations for a logarithmic number of rounds。 因此，只有当 m m m很大时，才有必要增加round complexity。 且本文Verifier端的工作非常轻量级。

3.1 相关技术

Groth 2009年论文[Gro09]《Linear algebra with sub-linear zero-knowledge arguments》中提出了 efficient sublinear size arguments to be used in connection with linear algebra over a finite field。本文将该技术与[GI08]中的sublinear size shuffle argument结合，构建了 an efficient multi-exponentiation argument that a ciphertext C C C is the product of a set of known ciphertexts C 1 , ⋯   , C N C_1,\cdots,C_N C1​,⋯,CN​ raised to a set of hidden committed values a 1 , ⋯   , a N a_1,\cdots,a_N a1​,⋯,aN​。

shuffle of ciphertexts的相关思路有：

• Neff [Nef01] 2001年论文《A verifiable secret shuffle and its application to e-voting》中的核心思路为：the invariance of polynomials P ( X ) = ∏ i = 1 N ( m i − X ) P(X)=\prod_{i=1}^{N}(m_i-X) P(X)=∏i=1N​(mi​−X) under permutation of roots。
• Groth [Gro10] 2010年论文《A verifiable secret shuffle of homomorphic encryptions》中的核心思想也为：the invariance of polynomials P ( X ) = ∏ i = 1 N ( m i − X ) P(X)=\prod_{i=1}^{N}(m_i-X) P(X)=∏i=1N​(mi​−X) under permutation of roots。
• Stamer [Sta05] 2005年论文《 Efficient electronic gambling: An extended implementation of the toolbox for mental card games》中做了相应的实现。
• Groth和Ishai 2008年论文[GI08]《Sub-linear zero-knowledge argument for correctness of a shuffle》中第一个实现了communication complexity为sublinear in the number of cipertexts的shuffle argument。

3.2 shuffle argument

针对的场景为：

• public info：ciphertexts { C i } i = 1 N , { C i ′ } i = 1 N \{C_i\}_{i=1}^{N},\{C_i'\}_{i=1}^{N} {Ci​}i=1N​,{Ci′​}i=1N​
• witness：permutation π ∈ ∑ N \pi\in\sum_N π∈∑N​, randomness { ρ i } i = 1 N \{\rho_i\}_{i=1}^{N} {ρi​}i=1N​
• relation： C i ′ = C π ( i ) ε p k ( 1 ; ρ i ) C_i'=C_{\pi(i)}\varepsilon_{pk}(1;\rho_i) Ci′​=Cπ(i)​εpk​(1;ρi​)

shuffle argument中主要包含了两个子argument：

• multi-exponenetiation argument
• product argument （参见博客 Practical Zero-Knowledge Protocols Based on the Discrete Logarithm Assumption 学习笔记 1 “5.3 product argument”）

shuffle argument的证明思路为：

• Prover: commit to the permutation，即commit to π ( 1 ) , ⋯   , π ( N ) \pi(1),\cdots,\pi(N) π(1),⋯,π(N)。【需证明相应的openings为 1 , ⋯   , N 1,\cdots,N 1,⋯,N的permutation。】
• Verifier：发送challenge x x x。
• Prover：commit to x π ( 1 ) , ⋯   , x π ( N ) x^{\pi(1)},\cdots,x^{\pi(N)} xπ(1),⋯,xπ(N)。【需证明相应的openings为 x 1 , ⋯   , x N x^1,\cdots,x^N x1,⋯,xN的permutation。且两组permutation为完全相同的，即the prover has a commitment to x 1 , ⋯   , x N x^1,\cdots,x^N x1,⋯,xN permutated in an order that was fixed before the prover saw x x x。】
• Verifier：为了证明两组commitments采用的是相同的permutation，Verifier发送challenges y , z y,z y,z。
• Prover：构建 d 1 − z = y π ( 1 ) + x π ( 1 ) − z , ⋯   , d N − z = y π ( N ) + x π ( N ) − z d_1-z=y\pi(1)+x^{\pi(1)}-z,\cdots,d_N-z=y\pi(N)+x^{\pi(N)}-z d1​−z=yπ(1)+xπ(1)−z,⋯,dN​−z=yπ(N)+xπ(N)−z 转为证明 ∏ i = 1 N ( d i − z ) = ∏ i = 1 N ( y i + x i − z ) \prod_{i=1}^{N}(d_i-z)=\prod_{i=1}^{N}(yi+x^i-z) ∏i=1N​(di​−z)=∏i=1N​(yi+xi−z) 【可利用 博客 Practical Zero-Knowledge Protocols Based on the Discrete Logarithm Assumption 学习笔记 1 中的 “single value product argument for public b b b” 来证明。】 1）可将其看成是基于 z z z变量的多项式，将 y i + x i yi+x^i yi+xi 看成是多项式的根。 基于Schwartz-Zippel lemma可知，对于随机选择的 z z z，等式成立的概率可忽略。 2）而permutation π \pi π可表示为： d 1 = y π ( 1 ) + x π ( 1 ) , ⋯   , d N = y π ( N ) + x π ( N ) d_1=y\pi(1)+x^{\pi(1)},\cdots,d_N=y\pi(N)+x^{\pi(N)} d1​=yπ(1)+xπ(1),⋯,dN​=yπ(N)+xπ(N) Furthermore, there is negligible probability over the choice of y y y of this being true unless the first commitment contains π ( 1 ) , ⋯   , π ( N ) \pi(1),\cdots,\pi(N) π(1),⋯,π(N) and the second commitment contains x π ( 1 ) , ⋯   , x π ( N ) x^{\pi(1)},\cdots,x^{\pi(N)} xπ(1),⋯,xπ(N)。 3）Prover commit to x π ( 1 ) , ⋯   , x π ( N ) x^{\pi(1)},\cdots,x^{\pi(N)} xπ(1),⋯,xπ(N)，利用multi-exponentiation argument来证明存在 ρ \rho ρ 使得： ∏ i = 1 N C i x i = ε p k ( 1 ; ρ ) ∏ i = 1 N ( C i ′ ) x π ( i ) \prod_{i=1}^{N}C_i^{x^i}=\varepsilon_{pk}(1;\rho)\prod_{i=1}^{N}(C_i')^{x^{\pi(i)}} ∏i=1N​Cixi​=εpk​(1;ρ)∏i=1N​(Ci′​)xπ(i) Verifier不知道the committed values，因此也不知道what the permutation is。但是基于encryption scheme的同态属性，Verifier可推导： ∏ i = 1 N M i x i = ∏ i = 1 N ( M i ′ ) x π ( i ) \prod_{i=1}^{N}M_i^{x^i}=\prod_{i=1}^{N}(M_i')^{x^{\pi(i)}} ∏i=1N​Mixi​=∏i=1N​(Mi′​)xπ(i) for some permutation π \pi π that was chosen before the challenge x x x was sent to the prover。进行discrete logarithm计算，有the polynomial identity： ∑ i = 1 N log ⁡ ( M i ) x i = ∑ i = 1 N log ⁡ ( M π − 1 ( i ) ′ ) x i \sum_{i=1}^{N}\log (M_i)x^i=\sum_{i=1}^{N}\log(M_{\pi^{-1}(i)}')x^i ∑i=1N​log(Mi​)xi=∑i=1N​log(Mπ−1(i)′​)xi 因此，there is negligible probability over the choice of x x x of this equality holding true unless M 1 ′ = M π ( 1 ) , ⋯   , M N ′ = M π ( N ) M_1'=M_{\pi(1)},\cdots,M_{N}'=M_{\pi(N)} M1′​=Mπ(1)​,⋯,MN′​=Mπ(N)​

完整的证明过程为：

以上shuffle argument算法的效率分析为：

3.3 multi-exponentiation argument

针对的场景为：

• public info： { C i } i = 1 N , { C i ′ } i = 1 N , x \{C_i\}_{i=1}^N,\{C_i'\}_{i=1}^N,x {Ci​}i=1N​,{Ci′​}i=1N​,x 和 commitments { C π ( i ) } i = 1 N \{C_{\pi(i)}\}_{i=1}^N {Cπ(i)​}i=1N​
• private info： ρ , { π ( i ) } i = 1 N \rho,\{\pi(i)\}_{i=1}^{N} ρ,{π(i)}i=1N​
• relation： ∏ i = 1 N C i x i = ε p k ( 1 ; ρ ) ∏ i = 1 N ( C i ′ ) x π ( i ) \prod_{i=1}^{N}C_i^{x^i}=\varepsilon_{pk}(1;\rho)\prod_{i=1}^{N}(C_i')^{x^{\pi(i)}} ∏i=1N​Cixi​=εpk​(1;ρ)∏i=1N​(Ci′​)xπ(i) 以及 C π ( i ) = C o m c k ( π ( i ) ) C_{\pi(i)}=Com_{ck}(\pi(i)) Cπ(i)​=Comck​(π(i))

假设 N = m n N=mn N=mn，以 m × n m\times n m×n矩阵表示，将其扩展为更通用的情况为：【设 ∏ i = 1 N C i x i = C \prod_{i=1}^{N}C_i^{x^i}=C ∏i=1N​Cixi​=C， { π ( i ) } i = 1 N = A = { a i j } i , j = 1 m , n = ( a ⃗ 1 , ⋯   , a ⃗ m ) \{\pi(i)\}_{i=1}^{N}=\mathbf{A}=\{a_{ij}\}_{i,j=1}^{m,n}=(\vec{a}_1,\cdots,\vec{a}_m) {π(i)}i=1N​=A={aij​}i,j=1m,n​=(a 1​,⋯,a m​)， { ( C i ′ ) x } i = 1 N = { C i j } i , j = 1 m , n = c ⃗ 1 , ⋯   , c ⃗ m \{(C_i')^x\}_{i=1}^{N}=\{C_{ij}\}_{i,j=1}^{m,n}={\vec{c}_1,\cdots,\vec{c}_m} {(Ci′​)x}i=1N​={Cij​}i,j=1m,n​=c 1​,⋯,c m​】

• public info：commitments c ⃗ A \vec{c}_A c A​, C , c ⃗ 1 , ⋯   , c ⃗ m C,\vec{c}_1,\cdots,\vec{c}_m C,c 1​,⋯,c m​
• private info： ρ , r ⃗ , A = { a i j } i , j = 1 m , n = ( a ⃗ 1 , ⋯   , a ⃗ m ) \rho,\vec{r},\mathbf{A}=\{a_{ij}\}_{i,j=1}^{m,n}=(\vec{a}_1,\cdots,\vec{a}_m) ρ,r ,A={aij​}i,j=1m,n​=(a 1​,⋯,a m​)
• relation： c ⃗ A = C o m c k ( A ; r ⃗ ) = ( C o m c k ( a ⃗ 1 ; r 1 ) , ⋯   , C o m c k ( a ⃗ m ; r m ) ) \vec{c}_A=Com_{ck}(\mathbf{A};\vec{r})=(Com_{ck}(\vec{a}_1;r_1),\cdots,Com_{ck}(\vec{a}_m;r_m)) c A​=Comck​(A;r )=(Comck​(a 1​;r1​),⋯,Comck​(a m​;rm​)) 且 C = ε p k ( 1 ; ρ ) ∏ i = 1 m c ⃗ i a ⃗ i C=\varepsilon_{pk}(1;\rho)\prod_{i=1}^{m}\vec{c}_i^{\vec{a}_i} C=εpk​(1;ρ)∏i=1m​c ia i​​

为了简单起见，现考虑 ρ = 0 \rho=0 ρ=0的情况，即证明Prover know the openings of c ⃗ A \vec{c}_A c A​，满足 C = ∏ i = 1 m c ⃗ i a ⃗ i C=\prod_{i=1}^{m}\vec{c}_i^{\vec{a}_i} C=∏i=1m​c ia i​​。 以如下方式表示： 其中 E m = C E_m=C Em​=C， E k = ∏ 1 ≤ i , j ≤ m ; j = ( k − m ) + i c ⃗ i a ⃗ j E_k=\prod_{1\leq i,j\leq m;j=(k-m)+i}\vec{c}_i^{\vec{a}_j} Ek​=∏1≤i,j≤m;j=(k−m)+i​c ia j​​。 基本证明思路为：【 ρ = 0 \rho=0 ρ=0的情况下】

• Prover：将ciphertexts E 1 , ⋯   , E 2 m − 1 E_1,\cdots,E_{2m-1} E1​,⋯,E2m−1​ 发送给Verifier，其中 C = E m C=E_m C=Em​为主对角线上元素的乘积， E k E_k Ek​为其它对角线上的元素乘积。
• Verifier：发送 challenge x ← Z q ∗ x\leftarrow \mathbb{Z}_q^* x←Zq∗​。
• Prover：采用batch方式证明所有对角线上的元素乘积分别对应 E k E_k Ek​，方式为： 设置 x ⃗ = ( x , x 2 , ⋯   , x m ) T \vec{x}=(x,x^2,\cdots,x^m)^T x =(x,x2,⋯,xm)T Prover opens c ⃗ A x ⃗ \vec{c}_A^{\vec{x}} c Ax ​ to a ⃗ = ∑ j = 1 m x j a ⃗ j \vec{a}=\sum_{j=1}^{m}x^j\vec{a}_j a =∑j=1m​xja j​，即Prover将 a ⃗ \vec{a} a 发送给Verifier。 有： x m − i a ⃗ = x m a ⃗ i + ∑ j = 1 , j ≠ i m x m − i + j a ⃗ j = x m a ⃗ i + ∑ j = 1 , j ≠ i , k = m − i + j m x k a ⃗ j x^{m-i}\vec{a}=x^m\vec{a}_i+\sum_{j=1,j\neq i}^mx^{m-i+j}\vec{a}_j=x^m\vec{a}_i+\sum_{j=1,j\neq i,k=m-i+j}^mx^{k}\vec{a}_j xm−ia =xma i​+∑j=1,j​=im​xm−i+ja j​=xma i​+∑j=1,j​=i,k=m−i+jm​xka j​
• Verifier：验证 c ⃗ A x ⃗ = C o m c k ( a ⃗ ; r ) \vec{c}_A^{\vec{x}}=Com_{ck}(\vec{a};r) c Ax ​=Comck​(a ;r) 和 C x m ∏ k = 1 , k ≠ m 2 m − 1 E k x k = ∏ i = 1 m c ⃗ i ( x m − i a ⃗ ) C^{x^m}\prod_{k=1,k\neq m}^{2m-1}E_k^{x^k}=\prod_{i=1}^{m}\vec{c}_i^{(x^{m-i}\vec{a})} Cxm∏k=1,k​=m2m−1​Ekxk​=∏i=1m​c i(xm−ia )​ 即可。

zero-knowledge属性实现：

• 为了避免泄露information about the exponent vectors a ⃗ 1 , ⋯   , a ⃗ m \vec{a}_1,\cdots,\vec{a}_m a 1​,⋯,a m​，Prover引入了随机vector a ⃗ 0 ← Z q n \vec{a}_0\leftarrow \mathbb{Z}_q^n a 0​←Zqn​，首先commit to a ⃗ 0 \vec{a}_0 a 0​ 有 c A 0 = C o m c k ( a ⃗ 0 ; r 0 ) c_{A0}=Com_{ck}(\vec{a}_0;r_0) cA0​=Comck​(a 0​;r0​)，收到challenge x x x后，发送 a ⃗ = a ⃗ 0 + ∑ j = 1 m x j a ⃗ j \vec{a}=\vec{a}_0+\sum_{j=1}^{m}x^j\vec{a}_j a =a 0​+∑j=1m​xja j​ 给Verifier，Verifier验证： c A 0 c ⃗ A x ⃗ = C o m c k ( a ⃗ ; r ) c_{A0}\vec{c}_A^{\vec{x}}=Com_{ck}(\vec{a};r) cA0​c Ax ​=Comck​(a ;r)。
• Prvoer传输 E k = ∏ 1 ≤ i , j ≤ m ; j = ( k − m ) + i c ⃗ i a ⃗ j E_k=\prod_{1\leq i,j\leq m;j=(k-m)+i}\vec{c}_i^{\vec{a}_j} Ek​=∏1≤i,j≤m;j=(k−m)+i​c ia j​​ 时，也可能造成witness a ⃗ 1 , ⋯   , a ⃗ m \vec{a}_1,\cdots,\vec{a}_m a 1​,⋯,a m​ 的泄露，因此，可对每个 E k E_k Ek​乘以随机ciphertext ε p k ( G b k ; τ k ) \varepsilon_{pk}(G^{b_k};\tau_k) εpk​(Gbk​;τk​)，其中 b m = 0 b_m=0 bm​=0。Prover需先对 b k b_k bk​进行commit。

详细的zero-knowledge multi-exponentiation argument实现为：

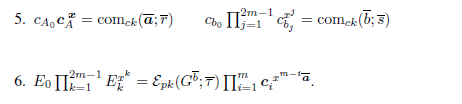
zero-knowledge multi-exponentiation argument的算法效率分析为： 相应的优化有：

• 1）优化Prover computation： 以上算法具有efficient verification 和 low communication complexity，但是Prover 需计算 E 0 , ⋯   , E 2 m − 1 E_0,\cdots,E_{2m-1} E0​,⋯,E2m−1​，不考虑zero-knowledge 实现引入的 E 0 E_0 E0​，只考虑 k = 1 , ⋯   , 2 m − 1 k=1,\cdots,2m-1 k=1,⋯,2m−1时： E k = ∏ i = 1 , j = 1 ; j = ( k − m ) + i m , m c ⃗ i a ⃗ j E_k=\prod_{i=1,j=1;j=(k-m)+i}^{m,m}\vec{c}_i^{\vec{a}_j} Ek​=∏i=1,j=1;j=(k−m)+im,m​c ia j​​ 为了计算 E k E_k Ek​，Prover需计算 m 2 m^2 m2 个product c i ⃗ a ⃗ j \vec{c_i}^{\vec{a}_j} ci​ ​a j​，而每一个 c ⃗ i a ⃗ j \vec{c}_i^{\vec{a}_j} c ia j​​的形式为： ∏ l = 1 n C i l a j l \prod_{l=1}^{n}C_{il}^{a_{jl}} ∏l=1n​Cilajl​​ 因此，最终计算 E k E_k Ek​ 需要 m 2 n m^2n m2n个exponentiations in H \mathbb{H} H。当 m m m很大时，计算量将很大。 可以借助multiplication of integers and polynomials的相关技术，如 Karatsuba [KO63]、Toom-Cook [Too00, Coo66] 以及 Fast Fourier Transform [CT65]。即： 为了计算两个 m − 1 m-1 m−1阶多项式的乘积 p ( x ) q ( x ) p(x)q(x) p(x)q(x)对应的系数，可evaluate p ( x ) q ( x ) p(x)q(x) p(x)q(x) in 2 m − 1 2m-1 2m−1 points w 0 , ⋯   , w 2 m − 2 w_0,\cdots,w_{2m-2} w0​,⋯,w2m−2​ ，然后借助多项式插值来恢复 the coefficients of p ( x ) q ( x ) p(x)q(x) p(x)q(x) from p ( w 0 ) q ( w 0 ) , ⋯   , p ( w 2 m − 2 ) q ( w 2 m − 2 ) p(w_0)q(w_0),\cdots,p(w_{2m-2})q(w_{2m-2}) p(w0​)q(w0​),⋯,p(w2m−2​)q(w2m−2​)。 但是FFT不适于与multi-exponentiation结合使用，当 m m m较小时，可借助Toom-Cook method for integer multiplication技术，选择 w 0 , w 1 , ⋯   , w 2 m − 2 w_0,w_1,\cdots,w_{2m-2} w0​,w1​,⋯,w2m−2​为small integers。当 m m m较小时，及时 w k 2 m − 2 w_k^{2m-2} wk2m−2​的也脚下。

• 2）trading computation for interaction： 借鉴Groth和Ishai 2008年论文[GI08]《Sub-linear zero-knowledge argument for correctness of a shuffle》 中的思路，不再计算矩阵中所有对角线的元素乘积，而只取主对角线上关联矩阵的对角线元素乘积进行证明。 trading computation for interaction的zero-knowledge multi-exponentiation argument算法实现为： trading computation for interaction的zero-knowledge multi-exponentiation argument算法的效率分析为：

4. 证明矩阵 M M M可逆