微软研究中心2020年论文《Spartan: Efficient and general-purpose zkSNARKs without trusted setup》，发表于Crypto 2020。
代码实现参见：
- https://github.com/microsoft/Spartan 【由Rust语言实现】
接下来，结合Vitalik Buterin博客Quardratic Arithmetic Programs: from Zero to Hero 中举例来做相应实现。
Spartan代码库中的 Z ⃗ \vec{Z} Z 布局为 [ v a r s → , 1 , i o → ] [\overrightarrow{vars},1,\overrightarrow{io}] [vars ,1,io ]，因此vitalik博客中的例子调整为：【其中 v a r s → \overrightarrow{vars} vars 对应为secret info， i o → \overrightarrow{io} io 对应为public info。】 Z ⃗ = [ x , s y m _ 1 , y , s y m _ 2 , ∼ o n e , ∼ o u t ] = [ 3 , 9 , 27 , 30 , 1 , 35 ] \vec{Z}=[x,sym\_1,y,sym\_2,\sim one,\sim out]=[3,9,27,30,1,35] Z =[x,sym_1,y,sym_2,∼one,∼out]=[3,9,27,30,1,35]。【其中 ∼ o u t = 35 \sim out=35 ∼out=35 为public input/output。】
对应的R1CS 矩阵 ( A , B , C ) (A,B,C) (A,B,C) 为： A = [ 1 0 0 0 0 0 0 1 0 0 0 0 1 0 1 0 0 0 0 0 0 1 5 0 ] A=\begin{bmatrix} 1 & 0 & 0 & 0 & 0& 0\\ 0 & 1 & 0 & 0 & 0& 0\\ 1 & 0 & 1 & 0 & 0& 0\\ 0 & 0 & 0 & 1 & 5& 0 \end{bmatrix} A=⎣ ⎡101001000010000100050000⎦ ⎤ B = [ 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 ] B=\begin{bmatrix} 1 & 0 & 0 & 0 & 0& 0\\ 1 & 0 & 0 & 0 & 0& 0\\ 0 & 0 & 0 & 0 & 1& 0\\ 0 & 0 & 0 & 0 &1& 0 \end{bmatrix} B=⎣ ⎡110000000000000000110000⎦ ⎤ C = [ 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 ] C=\begin{bmatrix} 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 \end{bmatrix} C=⎣ ⎡000010000100001000000001⎦ ⎤
2. 基本思路针对上述例子，对应的有：【注意max_nz_entries 表示矩阵A/B/C中的最大非零个数，用于决定generators的数量，不应限定为num_vars，而应是((num_cons * (num_vars + num_inputs + 1))as usize).next_power_of_two()。（为了使用Bulletproofs中的二分法，采用扩充0值的方式来实现power of two的要求。）】
let num_vars = 4; //secret info size
let num_cons = num_vars;
let num_inputs = 1; //public info size
let max_nz_entries = ((num_cons * (num_vars + num_inputs + 1))as usize).next_power_of_two(); //make it more general, for one constraint for A should have more than 1 zeros.
let num_poly_vars_x = num_cons.log2(); //2
let num_poly_vars_y = (2 * num_vars).log2(); //3
生成用于R1CS commit的public parameter gens_r1cs_eval: R1CSCommitmentGens，其中分别有gens_ops,gens_mem,gens_derefs 三大类generators。
/// `SNARKGens` holds public parameters for producing and verifying proofs with the Spartan SNARK
pub struct SNARKGens {
gens_r1cs_sat: R1CSGens,
gens_r1cs_eval: R1CSCommitmentGens,
}
pub struct R1CSCommitmentGens {
gens: SparseMatPolyCommitmentGens,
}
pub struct SparseMatPolyCommitmentGens {
gens_ops: PolyCommitmentGens,
gens_mem: PolyCommitmentGens,
gens_derefs: PolyCommitmentGens,
}
pub struct PolyCommitmentGens {
pub gens: DotProductProofGens,
}
pub struct DotProductProofGens {
n: usize,
pub gens_n: MultiCommitGens,
pub gens_1: MultiCommitGens,
}
#[derive(Debug)]
pub struct MultiCommitGens {
pub n: usize,
pub G: Vec,
pub h: GroupElement,
}
pub struct R1CSGens {
gens_sc: R1CSSumcheckGens,
gens_pc: PolyCommitmentGens,
}
pub struct R1CSSumcheckGens {
gens_1: MultiCommitGens, //generators数量为1
gens_3: MultiCommitGens, //generators数量为3+1个blind generator
gens_4: MultiCommitGens, //generators数量为4+1个blind generator
}
根据以上A/B/C/Z生成相应的R1CS instance：
let mut Z: Vec = Vec::new();
Z.push((3 as usize).to_scalar());
Z.push((9 as usize).to_scalar());
Z.push((27 as usize).to_scalar());
Z.push((30 as usize).to_scalar());
Z.push(Scalar::one());
Z.push((35 as usize).to_scalar());
println!("zyd Z: {:?}", Z);
// three sparse matrices
let mut A: Vec = Vec::new();
let mut B: Vec = Vec::new();
let mut C: Vec = Vec::new();
let one = Scalar::one();
A.push(SparseMatEntry::new(0, 0, one));
B.push(SparseMatEntry::new(0, 0, one));
C.push(SparseMatEntry::new(0, 1, one));
A.push(SparseMatEntry::new(1, 1, one));
B.push(SparseMatEntry::new(1, 0, one));
C.push(SparseMatEntry::new(1, 2, one));
A.push(SparseMatEntry::new(2, 2, one));
A.push(SparseMatEntry::new(2, 0, one));
B.push(SparseMatEntry::new(2, 4, one));
C.push(SparseMatEntry::new(2, 3, one));
A.push(SparseMatEntry::new(3, 3, one));
A.push(SparseMatEntry::new(3, 4, (5 as usize).to_scalar()));
B.push(SparseMatEntry::new(3, 4, one));
C.push(SparseMatEntry::new(3, 5, one));
let num_poly_vars_x = num_cons.log2();
let num_poly_vars_y = (2 * num_vars).log2();
let poly_A = SparseMatPolynomial::new(num_poly_vars_x, num_poly_vars_y, A);
let poly_B = SparseMatPolynomial::new(num_poly_vars_x, num_poly_vars_y, B);
let poly_C = SparseMatPolynomial::new(num_poly_vars_x, num_poly_vars_y, C);
let inst = R1CSInstance {
num_cons,
num_vars,
num_inputs,
A: poly_A,
B: poly_B,
C: poly_C,
};
assert_eq!(
inst.is_sat(&Z[..num_vars].to_vec(), &Z[num_vars + 1..].to_vec()),
true,
);
//(inst, vars, inputs)
(inst, Z[..num_vars].to_vec(), Z[num_vars + 1..].to_vec())
(inst, vars, inputs)封装为了：
Instance { inst },
VarsAssignment { assignment: vars },
InputsAssignment { assignment: inputs },
num_cells = 2 max { num_poly_vars_x , num_poly_vars_y } \text{num\_cells}=2^{\text{max}\{\text{num\_poly\_vars\_x}, \text{num\_poly\_vars\_y}\}} num_cells=2max{num_poly_vars_x,num_poly_vars_y} //8 N = max(A中非零个数,B中非零个数,C中非零个数).next_power_of_two() N=\text{max(A中非零个数,B中非零个数,C中非零个数).next\_power\_of\_two()} N=max(A中非零个数,B中非零个数,C中非零个数).next_power_of_two() // 6.next_power_of_two()=8
- 将A/B/C矩阵中的非零值
v
a
l
val
val 及所对应的坐标
(
i
,
j
)
(i,j)
(i,j) 分别存储在矩阵
ops_row_vec,ops_col_vec,val_vec中，有： ops_row_vec = [ 0 1 2 2 3 3 0 0 0 1 2 3 0 0 0 0 0 1 2 3 0 0 0 0 ] = [ R 1 ( y 1 , y 2 , y 3 ) R 2 ( y 1 , y 2 , y 3 ) R 3 ( y 1 , y 2 , y 3 ) ] \text{ops\_row\_vec}=\begin{bmatrix} 0 & 1 & 2 & 2 & 3& 3 & 0 & 0\\ 0 & 1 & 2 & 3 & 0& 0 & 0 & 0\\ 0 & 1 & 2 & 3 & 0& 0 & 0 & 0 \end{bmatrix}=\begin{bmatrix} R_1(y_1,y_2,y_3)\\ R_2(y_1,y_2,y_3)\\ R_3(y_1,y_2,y_3) \end{bmatrix} ops_row_vec=⎣ ⎡000111222233300300000000⎦ ⎤=⎣ ⎡R1(y1,y2,y3)R2(y1,y2,y3)R3(y1,y2,y3)⎦ ⎤ ops_col_vec = [ 0 1 2 0 3 4 0 0 0 0 4 4 0 0 0 0 1 2 3 5 0 0 0 0 ] = [ C 1 ( y 1 , y 2 , y 3 ) C 2 ( y 1 , y 2 , y 3 ) C 3 ( y 1 , y 2 , y 3 ) ] \text{ops\_col\_vec}=\begin{bmatrix} 0 & 1 & 2 & 0 & 3& 4 & 0 & 0\\ 0 & 0 & 4 & 4 & 0& 0 & 0 & 0\\ 1 & 2 & 3 & 5 & 0& 0 & 0 & 0 \end{bmatrix}=\begin{bmatrix} C_1(y_1,y_2,y_3)\\ C_2(y_1,y_2,y_3)\\ C_3(y_1,y_2,y_3) \end{bmatrix} ops_col_vec=⎣ ⎡001102243045300400000000⎦ ⎤=⎣ ⎡C1(y1,y2,y3)C2(y1,y2,y3)C3(y1,y2,y3)⎦ ⎤ val_vec = [ 1 1 1 1 1 5 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 ] = [ V 1 ( y 1 , y 2 , y 3 ) V 2 ( y 1 , y 2 , y 3 ) V 3 ( y 1 , y 2 , y 3 ) ] \text{val\_vec}=\begin{bmatrix} 1 & 1 & 1 & 1 & 1& 5 & 0 & 0\\ 1 & 1 & 1 & 1 & 0& 0 & 0 & 0\\ 1 & 1 & 1 & 1 & 0& 0 & 0 & 0 \end{bmatrix}=\begin{bmatrix} V_1(y_1,y_2,y_3)\\ V_2(y_1,y_2,y_3)\\ V_3(y_1,y_2,y_3) \end{bmatrix} val_vec=⎣ ⎡111111111111100500000000⎦ ⎤=⎣ ⎡V1(y1,y2,y3)V2(y1,y2,y3)V3(y1,y2,y3)⎦ ⎤ 其中： 1）将val_vec中的每一行以multilinear 多项式来表示。 2）将ops_row_vec和ops_col_vec中的每一行也以multilinear多项式，分别存储在row和col中的ops_addr中；而原始的ops_row_vec和ops_col_vec矩阵则直接分别存储在row和col中的ops_addr_usize中。 3）对ops_row_vec和ops_col_vec实现memory in head，引入了read_ts和audit_ts，其中read_ts是指在矩阵该位置的值在相应矩阵中出现的次数（不含当前次数），audit_ts则记录的依次为数字 0 , ⋯ , N − 1 0,\cdots,N-1 0,⋯,N−1 在相应的行 R i R_i Ri或 C i C_i Ci中出现的次数。read_ts矩阵中的每一行都会以multilinear 多项式表示，而audit_ts只取最后一行以multilinear 多项式表示（audit_ts记录数字 0 , ⋯ , N − 1 0,\cdots,N-1 0,⋯,N−1 在整个相应矩阵中出现的次数。）。 ops_row_vec = [ 0 1 2 2 3 3 0 0 0 1 2 3 0 0 0 0 0 1 2 3 0 0 0 0 ] row_read_ts = [ 0 0 0 1 0 1 1 2 3 1 2 2 4 5 6 7 8 2 3 3 9 10 11 12 ] row_audit_ts = [ 3 1 2 2 0 0 0 0 8 2 3 3 0 0 0 0 13 3 4 4 0 0 0 0 ] \text{ops\_row\_vec}=\begin{bmatrix} 0 & 1 & 2 & 2 & 3& 3 & 0 & 0\\ 0 & 1 & 2 & 3 & 0& 0 & 0 & 0\\ 0 & 1 & 2 & 3 & 0& 0 & 0 & 0 \end{bmatrix}\ \text{row\_read\_ts}=\begin{bmatrix} 0 & 0 & 0 & 1 & 0& 1 & 1 & 2\\ 3 & 1 & 2 & 2 & 4& 5 & 6 & 7\\ 8 & 2 & 3 & 3 & 9& 10 & 11 & 12 \end{bmatrix}\ \text{row\_audit\_ts}=\begin{bmatrix} 3 & 1 & 2 & 2 & 0& 0 & 0 & 0\\ 8 & 2 & 3 & 3 & 0& 0 & 0 & 0\\ 13 & 3 & 4 & 4 & 0& 0 & 0 & 0 \end{bmatrix} ops_row_vec=⎣ ⎡000111222233300300000000⎦ ⎤ row_read_ts=⎣ ⎡038012023123049151016112712⎦ ⎤ row_audit_ts=⎣ ⎡3813123234234000000000000⎦ ⎤ ops_col_vec = [ 0 1 2 0 3 4 0 0 0 0 4 4 0 0 0 0 1 2 3 5 0 0 0 0 ] col_read_ts = [ 0 0 0 1 0 0 2 3 4 5 1 2 6 7 8 9 1 1 1 0 10 11 12 13 ] col_audit_ts = [ 4 1 1 1 1 0 0 0 10 1 1 1 3 0 0 0 14 2 2 2 3 1 0 0 ] \text{ops\_col\_vec}=\begin{bmatrix} 0 & 1 & 2 & 0 & 3& 4 & 0 & 0\\ 0 & 0 & 4 & 4 & 0& 0 & 0 & 0\\ 1 & 2 & 3 & 5 & 0& 0 & 0 & 0 \end{bmatrix}\ \text{col\_read\_ts}=\begin{bmatrix} 0 & 0 & 0 & 1 & 0& 0 & 2 & 3\\ 4 & 5 & 1 & 2 & 6& 7 & 8 & 9\\ 1 & 1 & 1 & 0 & 10& 11 & 12 & 13 \end{bmatrix}\ \text{col\_audit\_ts}=\begin{bmatrix} 4 & 1 & 1 & 1 & 1& 0 & 0 & 0\\ 10 & 1 & 1 & 1 & 3& 0 & 0 & 0\\ 14 & 2 & 2 & 2 & 3& 1 & 0 & 0 \end{bmatrix} ops_col_vec=⎣ ⎡001102243045300400000000⎦ ⎤ col_read_ts=⎣ ⎡0410510111200610071128123913⎦ ⎤ col_audit_ts=⎣ ⎡41014112112112133001000000⎦ ⎤ 4）最终会将ops_row_vec,row_read_ts,ops_col_vec,col_read_ts,val_vec依次拉开拼接为一个（(5N*3).next_power_of_2()）vector，以multilinear 多项式comb_ops表示。//128 comb_ops = [ 0 , 1 , 2 , 2 , 3 , 3 , 0 , 0 , 0 , 1 , 2 , 3 , 0 , 0 , 0 , 0 , 0 , 1 , 2 , 3 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 1 , 0 , 1 , 1 , 2 , 3 , 1 , 2 , 2 , 4 , 5 , 6 , 7 , 8 , 2 , 3 , 3 , 9 , 10 , 11 , 12 , 0 , 1 , 2 , 0 , 3 , 4 , 0 , 0 , 0 , 0 , 4 , 4 , 0 , 0 , 0 , 0 , 1 , 2 , 3 , 5 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 1 , 0 , 0 , 2 , 3 , 4 , 5 , 1 , 2 , 6 , 7 , 8 , 9 , 1 , 1 , 1 , 0 , 10 , 11 , 12 , 13 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 ] \text{comb\_ops}=[0 ,1 ,2 ,2 ,3, 3 , 0 , 0, 0 ,1 ,2 , 3 , 0, 0 , 0 , 0, 0 , 1 , 2 ,3 ,0, 0 , 0 , 0, 0 , 0 , 0 , 1 , 0, 1 , 1 , 2, 3 , 1 , 2 , 2 , 4, 5 , 6 , 7, 8 , 2 , 3 , 3 , 9, 10 , 11 , 12, 0 , 1 ,2 , 0 , 3, 4 , 0 , 0, 0 , 0 , 4 , 4 , 0,0 , 0 , 0, 1 , 2 , 3 ,5 , 0, 0 , 0 , 0, 0 , 0 , 0 , 1 , 0,0 , 2 , 3, 4 , 5 , 1 , 2 , 6, 7 , 8 , 9, 1 , 1 , 1 , 0 , 10, 11 , 12 , 13, 0,0,0,0,0,0,0,0] comb_ops=[0,1,2,2,3,3,0,0,0,1,2,3,0,0,0,0,0,1,2,3,0,0,0,0,0,0,0,1,0,1,1,2,3,1,2,2,4,5,6,7,8,2,3,3,9,10,11,12,0,1,2,0,3,4,0,0,0,0,4,4,0,0,0,0,1,2,3,5,0,0,0,0,0,0,0,1,0,0,2,3,4,5,1,2,6,7,8,9,1,1,1,0,10,11,12,13,0,0,0,0,0,0,0,0] 将row_audit_ts,col_audit_ts拼接为一个（(2N).next_power_of_2()）vector，以multilinear多项式comb_mem表示。//16 comb_mem = [ 13 , 3 , 4 , 4 , 0 , 0 , 0 , 0 , 14 , 2 , 2 , 2 , 3 , 1 , 0 , 0 ] \text{comb\_mem}=[13, 3 , 4 , 4 , 0, 0, 0 , 0,14 , 2, 2, 2, 3, 1 , 0 , 0] comb_mem=[13,3,4,4,0,0,0,0,14,2,2,2,3,1,0,0]
// combine polynomials into a single polynomial for commitment purposes
let comb_ops = DensePolynomial::merge(
row
.ops_addr
.iter()
.chain(row.read_ts.iter())
.chain(col.ops_addr.iter())
.chain(col.read_ts.iter())
.chain(val_vec.iter()),
);
let mut comb_mem = row.audit_ts.clone();
comb_mem.extend(&col.audit_ts);
MultiSparseMatPolynomialAsDense {
batch_size: sparse_polys.len(),
row,
col,
val: val_vec,
comb_ops,
comb_mem,
}
MultiSparseMatPolynomialAsDense {
batch_size: sparse_polys.len(),
row,
col,
val: val_vec,
comb_ops,
comb_mem,
}
- 对
comb_ops和comb_mem分别进行 commit，最终有L_size个vector commitment，其中每个vector size为R_size。//(8;16) (4;4)
(
SparseMatPolyCommitment {
batch_size,
num_mem_cells: dense.row.audit_ts.len(), //8
num_ops: dense.row.read_ts[0].len(), //8
comm_comb_ops,
comm_comb_mem,
}, //公有信息
dense, //Prover私有信息
)
将以上公有信息封装为R1CSCommitment，并再次封装为ComputationCommitment，有：
let r1cs_comm = R1CSCommitment {
num_cons: self.num_cons,
num_vars: self.num_vars,
num_inputs: self.num_inputs,
comm,
};
comm = ComputationCommitment { r1cs_comm };
将Prover私有信息封装为R1CSDecommitment，并再次封装为ComputationDecommitment，有：
let r1cs_decomm = R1CSDecommitment { dense };
decomm = ComputationDecommitment { r1cs_decomm };
输入为public info以及 inst,dense,vars等私有信息。其中vars= Z[..num_vars].to_vec()。
- 基于
vars构建multilinear多项式，并对该multilinear多项式进行commit。
// create a multilinear polynomial using the supplied assignment for variables
let poly_vars = DensePolynomial::new(vars.clone());
// produce a commitment to the satisfying assignment
let (comm_vars, blinds_vars) = poly_vars.commit(&gens.gens_pc, Some(random_tape));
-
将通过pad 0的方式，使 Z ⃗ \vec{Z} Z 的length为power_of_two()，即为： Z ⃗ = [ 3 , 9 , 27 , 30 , 1 , 35 , 0 , 0 ] \vec{Z}=[3,9,27,30,1,35,0,0] Z =[3,9,27,30,1,35,0,0]
-
Prover：计算 A ∗ z ⃗ , B ∗ z ⃗ , C ∗ z ⃗ A*\vec{z},B*\vec{z},C*\vec{z} A∗z ,B∗z ,C∗z ，分别以multilinear多项式
poly_Az,poly_Bz,poly_Cz表示。 poly_Az=[3,9,30,35] poly_Bz=[3,3,1,1] poly_Cz=[9,27,30,35] -
Verifier：发送random evaluation vector (如 t ⃗ = [ t 1 , t 2 ] \vec{t}=[t_1,t_2] t =[t1,t2])，将该vector
evals()扩展（如 [ ( 1 − t 1 ) ( 1 − t 2 ) , ( 1 − t 1 ) t 2 , t 1 ( 1 − t 2 ) , t 1 t 2 ] [(1-t_1)(1-t_2),(1-t_1)t_2,t_1(1-t_2),t_1t_2] [(1−t1)(1−t2),(1−t1)t2,t1(1−t2),t1t2]）后以multilinear 多项式poly_tau表示。 呼应Spartan论文中的公式：
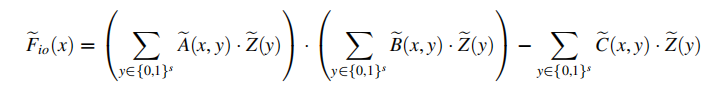
对应为Spartan 论文中的第5步：
sum-check protocol 具体算法思路可参见博客 sum-check protocol in zkproof 中“5.2 reduce cost版 zero-knowledge sum-check protocol”。
从第1轮到num_rounds_x轮，在每一轮中：【注意其中poly_tau,poly_Az,poly_Bz,poly_Cz均为mut，其内容在每一轮均会改变。】
- Prover： 取
len=poly_tau.len()/2，claim_per_round=0，计算： eval_point_0 = ∑ i = 0 l e n − 1 poly_tau [ i ] ∗ ( poly_Az [ i ] ∗ poly_Bz [ i ] − poly_Cz [ i ] ) \text{eval\_point\_0}=\sum_{i=0}^{len-1}\text{poly\_tau}[i]*(\text{poly\_Az}[i]*\text{poly\_Bz}[i]-\text{poly\_Cz}[i]) eval_point_0=∑i=0len−1poly_tau[i]∗(poly_Az[i]∗poly_Bz[i]−poly_Cz[i])【若正确应为0】 eval_point_2 = ∑ i = 0 l e n − 1 ( 2 ∗ poly_tau [ l e n + i ] − poly_tau [ i ] ) ∗ ( ( 2 ∗ poly_Az [ l e n + i ] − poly_Az [ i ] ) ∗ ( 2 ∗ poly_Bz [ l e n + i ] − poly_Bz [ i ] ) − ( 2 ∗ poly_Cz [ l e n + i ] − poly_Cz [ i ] ) ) \text{eval\_point\_2}=\sum_{i=0}^{len-1}(2*\text{poly\_tau}[len+i]-\text{poly\_tau}[i])*((2*\text{poly\_Az}[len+i]-\text{poly\_Az}[i])*(2*\text{poly\_Bz}[len+i]-\text{poly\_Bz}[i])-(2*\text{poly\_Cz}[len+i]-\text{poly\_Cz}[i])) eval_point_2=∑i=0len−1(2∗poly_tau[len+i]−poly_tau[i])∗((2∗poly_Az[len+i]−poly_Az[i])∗(2∗poly_Bz[len+i]−poly_Bz[i])−(2∗poly_Cz[len+i]−poly_Cz[i])) eval_point_3 = ∑ i = 0 l e n − 1 ( 3 ∗ poly_tau [ l e n + i ] − 2 ∗ poly_tau [ i ] ) ∗ ( ( 3 ∗ poly_Az [ l e n + i ] − 2 ∗ poly_Az [ i ] ) ∗ ( 3 ∗ poly_Bz [ l e n + i ] − 2 ∗ poly_Bz [ i ] ) − ( 3 ∗ poly_Cz [ l e n + i ] − 2 ∗ poly_Cz [ i ] ) ) \text{eval\_point\_3}=\sum_{i=0}^{len-1}(3*\text{poly\_tau}[len+i]-2*\text{poly\_tau}[i])*((3*\text{poly\_Az}[len+i]-2*\text{poly\_Az}[i])*(3*\text{poly\_Bz}[len+i]-2*\text{poly\_Bz}[i])-(3*\text{poly\_Cz}[len+i]-2*\text{poly\_Cz}[i])) eval_point_3=∑i=0len−1(3∗poly_tau[len+i]−2∗poly_tau[i])∗((3∗poly_Az[len+i]−2∗poly_Az[i])∗(3∗poly_Bz[len+i]−2∗poly_Bz[i])−(3∗poly_Cz[len+i]−2∗poly_Cz[i])) 构建向量[eva_point_0, claim_per_round-eval_point_0, eval_point_2, eval_point_3]，以单变量多项式poly= a x 3 + b x 2 + c x + d =ax^3+bx^2+cx+d =ax3+bx2+cx+d 表示，并对其进行commitcomm_poly。
【 以2变量multilinear多项式为例，以上计算的原理为： G ( x 1 , x 2 ) = a 0 + a 1 x 1 + a 2 x 2 + a 3 x 1 x 2 G(x_1,x_2)=a_0+a_1x_1+a_2x_2+a_3x_1x_2 G(x1,x2)=a0+a1x1+a2x2+a3x1x2 有： G ( 0 , 0 ) = a 0 ; G ( 0 , 1 ) = a 0 + a 2 ; G ( 1 , 0 ) = a 0 + a 1 ; G ( 1 , 1 ) = a 0 + a 1 + a 2 + a 3 G(0,0)=a_0;G(0,1)=a_0+a_2;G(1,0)=a_0+a_1;G(1,1)=a_0+a_1+a_2+a_3 G(0,0)=a0;G(0,1)=a0+a2;G(1,0)=a0+a1;G(1,1)=a0+a1+a2+a3 G 1 ( x 1 ) = G ( x 1 , 0 ) + G ( x 2 , 0 ) = a 0 + a 1 x 1 + a 0 + a 1 x 1 + a 2 + a 3 x 1 G_1(x_1)=G(x_1,0)+G(x_2,0)=a_0+a_1x_1+a_0+a_1x_1+a_2+a_3x_1 G1(x1)=G(x1,0)+G(x2,0)=a0+a1x1+a0+a1x1+a2+a3x1 则： G 1 ( 0 ) = G ( 0 , 0 ) + G ( 0 , 1 ) G_1(0)=G(0,0)+G(0,1) G1(0)=G(0,0)+G(0,1) sumcheck协议中有： G 1 ( 1 ) + G 1 ( 0 ) = T G_1(1)+G_1(0)=T G1(1)+G1(0)=T，从而 G 1 ( 1 ) = T − G 1 ( 0 ) G_1(1)=T-G_1(0) G1(1)=T−G1(0) G 1 ( 2 ) = [ 2 G ( 1 , 0 ) − G ( 0 , 0 ) ] + [ 2 G ( 1 , 1 ) − G ( 0 , 1 ) ] G_1(2)=[2G(1,0)-G(0,0)]+[2G(1,1)-G(0,1)] G1(2)=[2G(1,0)−G(0,0)]+[2G(1,1)−G(0,1)] G 1 ( 3 ) = [ 3 G ( 1 , 0 ) − 2 G ( 0 , 0 ) ] + [ 3 G ( 1 , 1 ) − 2 G ( 0 , 1 ) ] G_1(3)=[3G(1,0)-2G(0,0)]+[3G(1,1)-2G(0,1)] G1(3)=[3G(1,0)−2G(0,0)]+[3G(1,1)−2G(0,1)] 】
-
Verifier： 发送random challenge r j r_j rj。
-
Prover： 1）bound all tables to the verifier’s challenge。【注意此处，
poly_tau,poly_Az,poly_Bz,poly_Cz内容将改变，其len在每一轮缩小一半。】【实际计算的就是sumcheck protocol中的： g 2 ( X 2 ) = ∑ ( x 3 , ⋯ , x v ) v − g ( r 1 , X 2 , x 3 , ⋯ , x v ) = c 0 , 2 + c 1 , 2 X 2 + c 2 , 2 X 2 2 g_2(X_2)=\sum_{(x_3,\cdots,x_v)^{v-}}g(r_1,X_2,x_3,\cdots,x_v)=c_{0,2}+c_{1,2}X_2+c_{2,2}X_2^2 g2(X2)=∑(x3,⋯,xv)v−g(r1,X2,x3,⋯,xv)=c0,2+c1,2X2+c2,2X22 ⋮ \vdots ⋮ g j ( X j ) = ∑ ( x j + 1 , ⋯ , x v ) v − j g ( r 1 , ⋯ , r j − 1 , X j , x j + 1 , ⋯ , x v ) = c 0 , j + c 1 , j X j + c 2 , j X j 2 g_j(X_j)=\sum_{(x_{j+1},\cdots,x_v)^{v-j}}g(r_1,\cdots,r_{j-1},X_j,x_{j+1},\cdots,x_v)=c_{0,j}+c_{1,j}X_j+c_{2,j}X_j^2 gj(Xj)=∑(xj+1,⋯,xv)v−jg(r1,⋯,rj−1,Xj,xj+1,⋯,xv)=c0,j+c1,jXj+c2,jXj2 】
// bound all tables to the verifier's challenege
poly_tau.bound_poly_var_top(&r_j);
poly_Az.bound_poly_var_top(&r_j);
poly_Bz.bound_poly_var_top(&r_j);
poly_Cz.bound_poly_var_top(&r_j);
pub fn bound_poly_var_top(&mut self, r: &Scalar) {
let n = self.len() / 2;
for i in 0..n {
self.Z[i] = self.Z[i] + r * (self.Z[i + n] - self.Z[i]);
}
self.num_vars -= 1;
self.len = n;
}
2）Prover：将每一轮的proof,commitment，以及challenge都记录上。
comm_polys.push(comm_poly);
.......
proofs.push(proof);
claim_per_round = claim_next_round;
comm_claim_per_round = comm_claim_next_round;
r.push(r_j);
comm_evals.push(comm_claim_per_round);
3）Prover：返回ZKSumcheckInstanceProof、challenges、最后一轮的evaluations 以及 最后一轮evaluation commitment的blindness值。其中poly_B[0]对应为sum-check protocol中最后一轮的 g v ( r v ) g_v(r_v) gv(rv)值，亦即 g ( r 1 , ⋯ , r v ) g(r_1,\cdots,r_v) g(r1,⋯,rv)值。
(
ZKSumcheckInstanceProof::new(comm_polys, comm_evals, proofs),
r,
vec![poly_A[0], poly_B[0], poly_C[0], poly_D[0]],
blinds_evals[num_rounds - 1],
)
具体可参见博客 Hyrax: Doubly-efficient zkSNARKs without trusted setup代码解析。
let (pok_Cz_claim, comm_Cz_claim) = {
KnowledgeProof::prove(
&gens.gens_sc.gens_1,
transcript,
random_tape,
&Cz_claim,
&Cz_blind,
)
};
let (proof_prod, comm_Az_claim, comm_Bz_claim, comm_prod_Az_Bz_claims) = {
let prod = Az_claim * Bz_claim;
ProductProof::prove(
&gens.gens_sc.gens_1,
transcript,
random_tape,
&Az_claim,
&Az_blind,
&Bz_claim,
&Bz_blind,
&prod,
&prod_Az_Bz_blind,
)
};
// prove the final step of sum-check #1
let taus_bound_rx = tau_claim;
let blind_expected_claim_postsc1 = taus_bound_rx * (prod_Az_Bz_blind - Cz_blind);
let claim_post_phase1 = (Az_claim * Bz_claim - Cz_claim) * taus_bound_rx;
let (proof_eq_sc_phase1, _C1, _C2) = EqualityProof::prove(
&gens.gens_sc.gens_1,
transcript,
random_tape,
&claim_post_phase1,
&blind_expected_claim_postsc1,
&claim_post_phase1,
&blind_claim_postsc1,
);
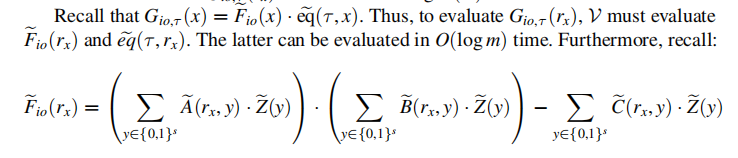至此，Verifier需自己计算
F
~
i
o
(
r
x
)
\tilde{F}_{io}(r_x)
F~io(rx) 和
e
q
~
(
τ
,
r
x
)
\tilde{eq}(\tau,r_x)
eq~(τ,rx)，其中
e
q
~
(
τ
,
r
x
)
\tilde{eq}(\tau,r_x)
eq~(τ,rx)的计算时间为
O
(
log
m
)
O(\log m)
O(logm)，而对于
F
~
i
o
(
r
x
)
\tilde{F}_{io}(r_x)
F~io(rx) 需分别计算：
∀
y
∈
{
0
,
1
}
s
:
A
~
(
r
x
,
y
)
,
B
~
(
r
x
,
y
)
,
C
~
(
r
x
,
y
)
,
Z
~
(
y
)
\forall y\in\{0,1\}^s: \tilde{A}(r_x,y),\tilde{B}(r_x,y),\tilde{C}(r_x,y),\tilde{Z}(y)
∀y∈{0,1}s:A~(rx,y),B~(rx,y),C~(rx,y),Z~(y)
其中 the evaluations of Z ~ ( y ) \tilde{Z}(y) Z~(y) for all y ∈ { 0 , 1 } s y\in\{0,1\}^s y∈{0,1}s 实际即为： ( w , 1 , i o ) (w,1,io) (w,1,io) 因此，the communication from P P P to V V V 为 ≥ O ( ∣ w ∣ ) \geq O(|w|) ≥O(∣w∣)。
可以将
∀
y
∈
{
0
,
1
}
s
:
A
~
(
r
x
,
y
)
,
B
~
(
r
x
,
y
)
,
C
~
(
r
x
,
y
)
\forall y\in\{0,1\}^s: \tilde{A}(r_x,y),\tilde{B}(r_x,y),\tilde{C}(r_x,y)
∀y∈{0,1}s:A~(rx,y),B~(rx,y),C~(rx,y) 的计算分别通过 sum-check protocol 委托给Prover来计算证明，不过，可引入随机数
r
A
,
r
B
,
r
C
r_A,r_B,r_C
rA,rB,rC 将三个sum-check protocol 合并为1个protocol来证明： 
对以下红框内容的代码实现为： 
// combine the three claims into a single claim
let r_A = transcript.challenge_scalar(b"challenege_Az");
let r_B = transcript.challenge_scalar(b"challenege_Bz");
let r_C = transcript.challenge_scalar(b"challenege_Cz");
let claim_phase2 = r_A * Az_claim + r_B * Bz_claim + r_C * Cz_claim;
let blind_claim_phase2 = r_A * Az_blind + r_B * Bz_blind + r_C * Cz_blind;
let evals_ABC = {
// compute the initial evaluation table for R(\tau, x)
let evals_rx = EqPolynomial::new(rx.clone()).evals();
let (evals_A, evals_B, evals_C) =
inst.compute_eval_table_sparse(inst.get_num_cons(), z.len(), &evals_rx);
assert_eq!(evals_A.len(), evals_B.len());
assert_eq!(evals_A.len(), evals_C.len());
(0..evals_A.len())
.map(|i| r_A * evals_A[i] + r_B * evals_B[i] + r_C * evals_C[i])
.collect::()
};
其中evals_A中记录的是：
A
~
(
r
x
,
0
,
0
,
⋯
,
0
)
,
⋯
,
A
~
(
r
x
,
1
,
1
,
⋯
,
1
)
\tilde{A}(r_x,0,0,\cdots,0),\cdots,\tilde{A}(r_x,1,1,\cdots,1)
A~(rx,0,0,⋯,0),⋯,A~(rx,1,1,⋯,1) 一系列的值，便于后续计算random
r
y
r_y
ry对应的
A
~
(
r
x
,
r
y
)
\tilde{A}(r_x,r_y)
A~(rx,ry)值。
// another instance of the sum-check protocol
let (sc_proof_phase2, ry, claims_phase2, blind_claim_postsc2) = R1CSProof::prove_phase_two(
num_rounds_y,
&claim_phase2,
&blind_claim_phase2,
&mut DensePolynomial::new(z),
&mut DensePolynomial::new(evals_ABC),
&gens.gens_sc,
transcript,
random_tape,
);
// prove_phase_two中实际证明的是：
L
(
r
x
)
=
∑
y
∈
{
0
,
1
}
s
[
r
A
⋅
A
~
(
r
x
,
y
)
+
r
B
⋅
B
~
(
r
x
,
y
)
+
r
C
⋅
C
~
(
r
x
,
y
)
]
⋅
Z
~
(
y
)
=
∑
y
∈
{
0
,
1
}
s
M
r
x
(
y
)
L(r_x)=\sum_{y\in\{0,1\}^s}[r_A\cdot\tilde{A}(r_x,y)+r_B\cdot\tilde{B}(r_x,y)+r_C\cdot\tilde{C}(r_x,y)]\cdot\tilde{Z}(y)=\sum_{y\in\{0,1\}^s} M_{r_x}(y)
L(rx)=∑y∈{0,1}s[rA⋅A~(rx,y)+rB⋅B~(rx,y)+rC⋅C~(rx,y)]⋅Z~(y)=∑y∈{0,1}sMrx(y) 因此其中定义的comb_func为： let comb_func = |poly_A_comp: &Scalar, poly_B_comp: &Scalar| -> Scalar { poly_A_comp * poly_B_comp };
fn prove_phase_two(
num_rounds: usize,
claim: &Scalar,
blind_claim: &Scalar,
evals_z: &mut DensePolynomial,
evals_ABC: &mut DensePolynomial,
gens: &R1CSSumcheckGens,
transcript: &mut Transcript,
random_tape: &mut RandomTape,
) -> (ZKSumcheckInstanceProof, Vec, Vec, Scalar) {
let comb_func =
|poly_A_comp: &Scalar, poly_B_comp: &Scalar| -> Scalar { poly_A_comp * poly_B_comp };
let (sc_proof_phase_two, r, claims, blind_claim_postsc) = ZKSumcheckInstanceProof::prove_quad(
claim,
blind_claim,
num_rounds,
evals_z,
evals_ABC,
comb_func,
&gens.gens_1,
&gens.gens_3,
transcript,
random_tape,
);
(sc_proof_phase_two, r, claims, blind_claim_postsc)
}
接2.4.4的内容，然后对以上sum-check protocol的最后一步进行证明：
// prove the final step of sum-check #2
let blind_eval_Z_at_ry = (Scalar::one() - ry[0]) * blind_eval;
let blind_expected_claim_postsc2 = claims_phase2[1] * blind_eval_Z_at_ry;
let claim_post_phase2 = claims_phase2[0] * claims_phase2[1];
let (proof_eq_sc_phase2, _C1, _C2) = EqualityProof::prove(
&gens.gens_pc.gens.gens_1,
transcript,
random_tape,
&claim_post_phase2,
&blind_expected_claim_postsc2,
&claim_post_phase2,
&blind_claim_postsc2,
);
借助2.3.3节的sum-check protocol的最后一轮，Verifier此时仍需要自己计算
M
r
x
(
r
y
)
M_{r_x}(r_y)
Mrx(ry) for
r
y
∈
F
s
r_y\in\mathbb{F}^s
ry∈Fs：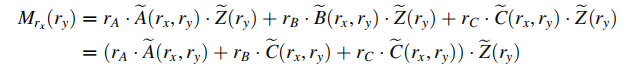 
注意以上
M
r
x
(
r
y
)
M_{r_x}(r_y)
Mrx(ry)中仅
Z
~
(
r
y
)
\tilde{Z}(r_y)
Z~(ry)中包含Prover witness信息，而其它项，Veriifer都可以利用
X
=
(
F
,
A
,
B
,
C
,
i
o
,
m
,
n
)
\mathbb{X}=(\mathbb{F},A,B,C,io,m,n)
X=(F,A,B,C,io,m,n)计算，计算用时为
O
(
n
)
O(n)
O(n)。【在Spartan论文第6章中，可将Verifier的该evaluation cost reduce为 sublinear in
n
n
n。】
接下来，对于 Z ~ ( r y ) \tilde{Z}(r_y) Z~(ry)，直观的证明是需要 O ( ∣ w ∣ ) O(|w|) O(∣w∣) communication cost，可借助extractable polynomial commitment scheme for multilinear polynomials 来证明 Z ~ ( r y ) \tilde{Z}(r_y) Z~(ry)，进一步reduce communication cost。 因此，可将 Z ~ ( r y ) \tilde{Z}(r_y) Z~(ry)拆分为两部分表示，secret witness部分 w ~ \tilde{w} w~ 和 public info部分 1 , i o ~ \widetilde{1,io} 1,io 来决定，具体为： Z ~ ( r y ) = ( 1 − r y [ 0 ] ) ⋅ w ~ ( r y [ 1.. ] ) + r y [ 0 ] ⋅ ( 1 , i o ) ~ ( r y [ 1.. ] ) \tilde{Z}(r_y)=(1-r_y[0])\cdot\tilde{w}(r_y[1..]) + r_y[0]\cdot\widetilde{(1,io)}(r_y[1..]) Z~(ry)=(1−ry[0])⋅w~(ry[1..])+ry[0]⋅(1,io) (ry[1..])
其中 w ~ ( ⋅ ) \tilde{w}(\cdot) w~(⋅)为witness的multilinear extension， ( 1 , i o ) ~ ( ⋅ ) \widetilde{(1,io)}(\cdot) (1,io) (⋅) 为public info的multilinear extension。
而
(
1
,
i
o
)
~
(
r
y
[
1..
]
)
\widetilde{(1,io)}(r_y[1..])
(1,io)
(ry[1..])可直接由Verifier计算： 
let poly_input_eval = {
// constant term
let mut input_as_sparse_poly_entries = vec![SparsePolyEntry::new(0, Scalar::one())];
//remaining inputs
input_as_sparse_poly_entries.extend(
(0..input.len())
.map(|i| SparsePolyEntry::new(i + 1, input[i]))
.collect::(),
);
SparsePolynomial::new(n.log2(), input_as_sparse_poly_entries).evaluate(&ry[1..].to_vec())
};
接下来，需由Prover来计算并证明 w ~ ( r y [ 1.. ] ) \tilde{w}(r_y[1..]) w~(ry[1..])：
- multilinear polynomial commitment： 在2.4.1 第一个sum-check protocol之前，Prover对 w ~ ( ⋅ ) \tilde{w}(\cdot) w~(⋅)进行commit，
let (poly_vars, comm_vars, blinds_vars) = {
// create a multilinear polynomial using the supplied assignment for variables
let poly_vars = DensePolynomial::new(vars.clone());
// produce a commitment to the satisfying assignment
let (comm_vars, blinds_vars) = poly_vars.commit(&gens.gens_pc, Some(random_tape));
// add the commitment to the prover's transcript
comm_vars.append_to_transcript(b"poly_commitment", transcript);
(poly_vars, comm_vars, blinds_vars)
};
- multilinear polynomial evaluation：
let eval_vars_at_ry = poly_vars.evaluate(&ry[1..].to_vec());
- multilinear polynomial prove：
let blind_eval = random_tape.random_scalar(b"blind_eval");
let (proof_eval_vars_at_ry, comm_vars_at_ry) = PolyEvalProof::prove(
&poly_vars,
Some(&blinds_vars),
&ry[1..].to_vec(),
&eval_vars_at_ry,
Some(&blind_eval),
&gens.gens_pc,
transcript,
random_tape,
);
依次对2.4节的各proof进行验证：
pub fn verify(
&self,
num_vars: usize,
num_cons: usize,
input: &[Scalar],
evals: &(Scalar, Scalar, Scalar),
transcript: &mut Transcript,
gens: &R1CSGens,
) -> Result {
transcript.append_protocol_name(R1CSProof::protocol_name());
let n = num_vars;
// add the commitment to the verifier's transcript
self
.comm_vars
.append_to_transcript(b"poly_commitment", transcript);
let (num_rounds_x, num_rounds_y) = (num_cons.log2(), (2 * num_vars).log2());
// derive the verifier's challenge tau
let tau = transcript.challenge_vector(b"challenge_tau", num_rounds_x);
// verify the first sum-check instance
let claim_phase1 = Scalar::zero()
.commit(&Scalar::zero(), &gens.gens_sc.gens_1)
.compress();
let (comm_claim_post_phase1, rx) = self.sc_proof_phase1.verify(
&claim_phase1,
num_rounds_x,
3,
&gens.gens_sc.gens_1,
&gens.gens_sc.gens_4,
transcript,
)?;
// perform the intermediate sum-check test with claimed Az, Bz, and Cz
let (comm_Az_claim, comm_Bz_claim, comm_Cz_claim, comm_prod_Az_Bz_claims) = &self.claims_phase2;
let (pok_Cz_claim, proof_prod) = &self.pok_claims_phase2;
assert!(pok_Cz_claim
.verify(&gens.gens_sc.gens_1, transcript, &comm_Cz_claim)
.is_ok());
assert!(proof_prod
.verify(
&gens.gens_sc.gens_1,
transcript,
&comm_Az_claim,
&comm_Bz_claim,
&comm_prod_Az_Bz_claims
)
.is_ok());
comm_Az_claim.append_to_transcript(b"comm_Az_claim", transcript);
comm_Bz_claim.append_to_transcript(b"comm_Bz_claim", transcript);
comm_Cz_claim.append_to_transcript(b"comm_Cz_claim", transcript);
comm_prod_Az_Bz_claims.append_to_transcript(b"comm_prod_Az_Bz_claims", transcript);
let taus_bound_rx: Scalar = (0..rx.len())
.map(|i| rx[i] * tau[i] + (Scalar::one() - rx[i]) * (Scalar::one() - tau[i]))
.product();
let expected_claim_post_phase1 = (taus_bound_rx
* (comm_prod_Az_Bz_claims.decompress().unwrap() - comm_Cz_claim.decompress().unwrap()))
.compress();
// verify proof that expected_claim_post_phase1 == claim_post_phase1
assert!(self
.proof_eq_sc_phase1
.verify(
&gens.gens_sc.gens_1,
transcript,
&expected_claim_post_phase1,
&comm_claim_post_phase1,
)
.is_ok());
// derive three public challenges and then derive a joint claim
let r_A = transcript.challenge_scalar(b"challenege_Az");
let r_B = transcript.challenge_scalar(b"challenege_Bz");
let r_C = transcript.challenge_scalar(b"challenege_Cz");
// r_A * comm_Az_claim + r_B * comm_Bz_claim + r_C * comm_Cz_claim;
let comm_claim_phase2 = GroupElement::vartime_multiscalar_mul(
iter::once(&r_A)
.chain(iter::once(&r_B))
.chain(iter::once(&r_C)),
iter::once(&comm_Az_claim)
.chain(iter::once(&comm_Bz_claim))
.chain(iter::once(&comm_Cz_claim))
.map(|pt| pt.decompress().unwrap())
.collect::(),
)
.compress();
// verify the joint claim with a sum-check protocol
let (comm_claim_post_phase2, ry) = self.sc_proof_phase2.verify(
&comm_claim_phase2,
num_rounds_y,
2,
&gens.gens_sc.gens_1,
&gens.gens_sc.gens_3,
transcript,
)?;
// verify Z(ry) proof against the initial commitment
assert!(self
.proof_eval_vars_at_ry
.verify(
&gens.gens_pc,
transcript,
&ry[1..].to_vec(),
&self.comm_vars_at_ry,
&self.comm_vars
)
.is_ok());
let poly_input_eval = {
// constant term
let mut input_as_sparse_poly_entries = vec![SparsePolyEntry::new(0, Scalar::one())];
//remaining inputs
input_as_sparse_poly_entries.extend(
(0..input.len())
.map(|i| SparsePolyEntry::new(i + 1, input[i]))
.collect::(),
);
SparsePolynomial::new(n.log2(), input_as_sparse_poly_entries).evaluate(&ry[1..].to_vec())
};
// compute commitment to eval_Z_at_ry = (Scalar::one() - ry[0]) * self.eval_vars_at_ry + ry[0] * poly_input_eval
let comm_eval_Z_at_ry = GroupElement::vartime_multiscalar_mul(
iter::once(Scalar::one() - ry[0]).chain(iter::once(ry[0])),
iter::once(&self.comm_vars_at_ry.decompress().unwrap()).chain(iter::once(
&poly_input_eval.commit(&Scalar::zero(), &gens.gens_pc.gens.gens_1),
)),
);
// perform the final check in the second sum-check protocol
let (eval_A_r, eval_B_r, eval_C_r) = evals;
let expected_claim_post_phase2 =
((r_A * eval_A_r + r_B * eval_B_r + r_C * eval_C_r) * comm_eval_Z_at_ry).compress();
// verify proof that expected_claim_post_phase2 == claim_post_phase2
assert!(self
.proof_eq_sc_phase2
.verify(
&gens.gens_sc.gens_1,
transcript,
&expected_claim_post_phase2,
&comm_claim_post_phase2,
)
.is_ok());
Ok((rx, ry))
}
}
- 博客 rank-1 constraint system R1CS
