通俗讲解支持向量机SVM（一）面试官：什么？线性模型你不会不清楚吧？

点赞再看，养成习惯，您动动手指对原创作者意义非凡🤝 备战2021秋招面试 微信搜索公众号【TechGuide】关注更多新鲜好文和互联网大厂的笔经面经。 作者@TechGuide

当你的才华还撑不起你的野心时，你应该静下心去学习 。

前言

大家好！这是我第一次使用csdn博客记录自己的学习历程，由于春招结尾，有一些碎片时间，而且最近毕业设计相关，恶补了不少算法知识，这篇学习笔记一者供自己复习巩固，二来或可给他人以帮助。

我在写这篇博文之前，也查阅学习了csdn的很多文章，内容已经非常详细，足够精彩，比如JULY的这篇支持向量机通俗导论（理解SVM的三层境界）

当然，我这里也会介绍全部SVM相关内容，但重点对SVM的提出思路和我在读文章过程中遇见的难点问题分享一些我自己的理解，意在让一些跟着SVM算法一路推导过来但还是对于细节有诸多疑问的朋友有新的理解。

千里之行，积于跬步，我将会竭力道出所想，欢迎大家交流指正。

支持向量机全系列

三个重点“间隔（margin）” “对偶(duality)” “核技巧(kernel trick)”,暂时不了解没关系，会一一引出。

没有免费午餐定理

此部分对于想节省时间的朋友可以略过 大名鼎鼎的没有免费午餐定理（No Free Lunch Theorem）对于理解很多概率统计的概念和动机有着至关重要的意义，它说明了对于预测来说先验概率存在的事实。

举个栗子，我们习惯性地判断寒冬过后，万物复苏，春暖花开，我们之所以做出这样的判断是基于我们对以往关于季节更替的历史数据有了所谓的“先验概率”，我们正是基于此有了“冬天之后是春天”的判断，试问，如果我们没有这个先验假设，冬之后是夏、春、秋、冬的概率应当是均等的。至此，我们得出结论： 如果没有对特征空间有先验假设，则所有算法的平均表现应当是相同的。

解释：特征空间即是指由春夏秋冬（可用1，2，3，4代替）组成的一维空间（也可更多维）； 算法是指对未来下一个季度作出判断的算法。

线性SVM模型 基础知识

我们知道Support Vector Machine(SVM)算法是由Support Vector Classifier（SVC）发展而来，这两者实际是包含的关系，SVM将样本分类的问题提到了更高维上，为什么这样做呢？很简单，对于低维度线性不可分的样本在高维度上就可能线性可分（实际上，无限维的样本必然线性可分）。

下图是对于一个在二维特征空间内的样本（红点与蓝点）利用线性模型分类的示意图。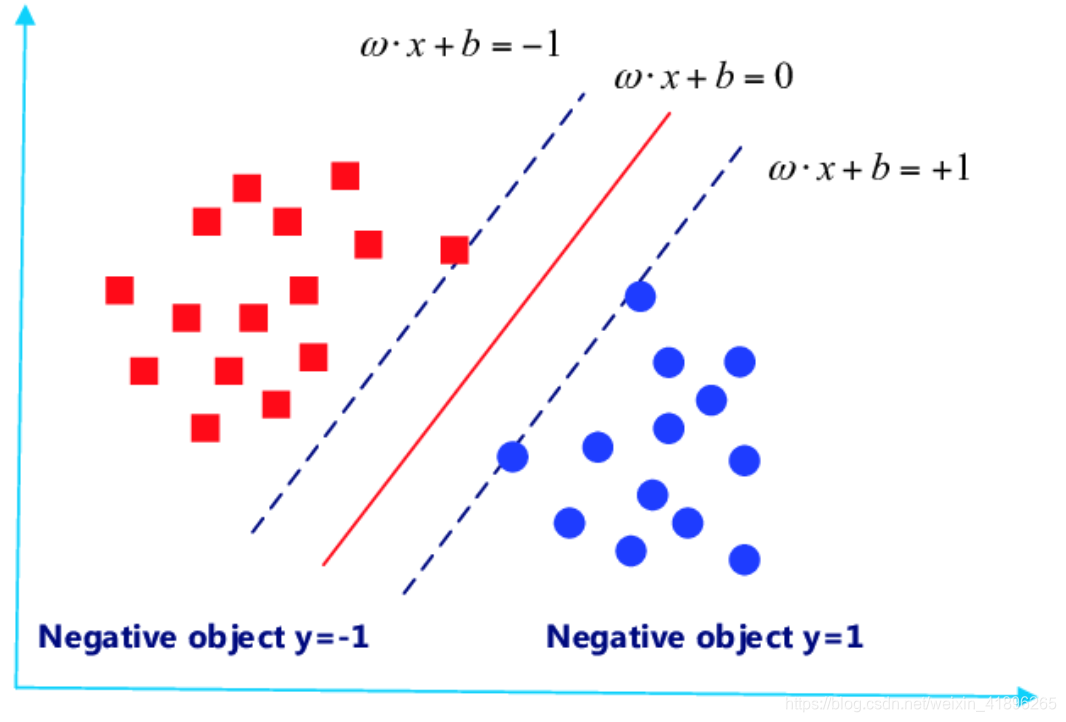

（source:https://www.researchgate.net/figure/Support-vector-machine-SVM-classifier_fig3_309361744）

据此，我们有几点说明(注意：以下我用大写字母表示向量，小写字母表示常数)：

• 每一个训练样本点可以用其特征向量和标签组成的一个坐标（Xi,yi）表示, 特征向量的概念很重要，它是指一个样本点有几个特征组成，比如图中的某一点X1=[X11,X12]T表示，而它的标签说明该点属于蓝或红，分别用1和-1表示；
• 那线性模型（红线）又是如何表示呢？ 很简单， 我们用WTX + b = 0表示，这里的权重W和特征向量X的维度是相同的。以此来分类，这个线性模型在以为特征空间是一个点，二维空间是一条线，三维空间是一个面，那四维及以上呢？我们无法描述，于是引进了超平面（hyperplane）的概念.
• 好，至此都很简单，接下来我们说一下线性模型的核心部分，即，如何定义一个训练集是线性可分的呢？我们是这样认为的，即， 存在（W,b）,使得 任意i = 1~N, 有 – if yi=+1, WTXi + b >= 0 – else yi=-1, WTXi + b < 0 以上我们可以用一个式子简化，即， 存在（W,b）,使得 任意i = 1~N, 有 yi *（WTXi + b ）>= 0 只要找到了这样一个（W,b）,我们就认为样本线性可分。

凸优化问题及间隔之引出

至此，我们说明了几个概念，接下来我再说明以下如何引出了凸优化问题的，我之前看的时候对于直接抛出来的优化问题和约束还是有诸多不解的。这里原原本本道清缘由。 首先，我们需要明白几点线性几何中的很简单的概念：

• WTXi + b = 0 和 aWTXi + ab = 0 是同一个（超）平面；
• 二维点(x0，y0)到平面w1x + w2y + b = 0距离公式为 d = |w1x0 + w2y0 + b| /(w12 + w22)1/2, 由此可联想向量X0到超平面WTXi + b = 0的距离公式为 d = |WTX0 + b| / ||W||

OK, 以上弄清楚了，我们就可以尝试分类以上两种样本点了，我们的目的是找到这样一条线（线性模型），使得两边的点距离这条线越远越好，也就是使这条线尽量居中，在线两侧获得足够大的裕度（margin），由此，我们得出我们的第一个优化问题初级版： Maxmize margin(W,b) subject to: For any i = 1~N, yi *（WTXi + b ）>= 0

解释一下，何谓最大化margin呢？也就是最大化离这条线最近的那个样本点到线的距离（这句话很重要，理解），这里我们给出一个概念，顺便点题，与这条线两侧近端最先擦到的特征向量即为支持向量，所以我们可以说目标函数是最大化支持向量（X0，y0）到线的距离，所以 margin(W,b) = Min distance(W,b,xi) = Min |WTX0 + b| / ||W|| 注意此处，我们可以用a缩放WTX0 + b，以期|WTX0 + b|=1。

上式可化为： Maxmize 1/||W|| subject to: For any i = 1~N, yi *（WTXi + b ）>= 1

解释一下，为什么约束条件变成大于1了呢？因为我们利用缩放使得|WTX0 + b|=1，这也是两条“相擦”（原谅我找不到更合适的词了）的线分别为WTXi + b = +1 和 WTXi + b = -1.

至此，我们可以得到凸优化问题最终版： Minimize 1/2||W||2(或者1/2WTW) subject to: For any i = 1~N, yi *（WTXi + b ）>= 1 说明一下，这里目标函数改成这种形式主要考虑求导运算简便一点,同时注意这里有N个限制条件，我们的目的是找出合适的W和b解出这个优化问题。

解凸优化问题及对偶问题之引出

这个部分重点不在于公式的详细推导，而是整体思路和脉络的把握，知其所以然。

我们得到上述优化问题形式后，可以“凝视”以下，看看该如何解，以及可不可解的问题。一般来说，对于一个目标函数是二次项，且约束条件为一次项的二次规划问题来说，其解要么只有一个，要么无解（可联想平面），good news!

第一步很常规，我们利用拉格朗日乘子法将带约束的凸优化问题转化成为无约束的凸优化问题。构造拉格朗日函数： L ( ω , b , λ ) = 1 2 ω T ω + ∑ i = 1 N λ i ( 1 − y i ( ω T X i + b ) ) , where λ i ≥ 0 (1) L(\omega,b,\lambda) = \frac{1}{2}\omega^T\omega + \sum_{i=1}^{N}\lambda_i(1-y_i(\omega^TX_i + b)) ,\text {where} \lambda_i \geq 0 \tag 1 L(ω,b,λ)=21​ωTω+i=1∑N​λi​(1−yi​(ωTXi​+b)),whereλi​≥0(1) 得到无约束的优化问题： min ⁡ w , b max ⁡ λ L ( ω , b , λ ) \min_{w,b} \max_{\lambda} L(\omega,b,\lambda) w,bmin​λmax​L(ω,b,λ) s.t. λ i ≥ 0 (2) \text{s.t.} \lambda_i \geq 0 \tag 2 s.t.λi​≥0(2) 此处稍微说明一下，其实很好理解， ∃ λ \exists \lambda ∃λ, 使得 L ( ω , b , λ ) L(\omega,b,\lambda) L(ω,b,λ)取得的最大值即为 1 2 ω T ω \frac{1}{2}\omega^T\omega 21​ωTω,因为 L ( ω , b , λ ) L(\omega,b,\lambda) L(ω,b,λ)后面那一项总是负的。

怎么解呢？这里我们引入对偶问题，通过对偶问题（dual problem）得到原问题（prime problem）的解,为什么这么做呢？因为更简便呀！

首先说一下什么是弱对偶关系。即： min ⁡ w , b max ⁡ λ L ( ω , b , λ ) ≥ max ⁡ λ min ⁡ w , b L ( ω , b , λ ) (3) \min_{w,b} \max_{\lambda} L(\omega,b,\lambda) \geq\max_{\lambda} \min_{w,b} L(\omega,b,\lambda) \tag 3 w,bmin​λmax​L(ω,b,λ)≥λmax​w,bmin​L(ω,b,λ)(3) 这个其实很好理解，“凤尾总是比鸡头强的”，严格证明也很简单，如下： min ⁡ w , b L ( ω , b , λ ) ≤ L ( ω , b , λ ) ≤ max ⁡ λ L ( ω , b , λ ) (4) \min_{w,b} L(\omega,b,\lambda) \leq L(\omega,b,\lambda) \leq \max_{\lambda} L(\omega,b,\lambda) \tag 4 w,bmin​L(ω,b,λ)≤L(ω,b,λ)≤λmax​L(ω,b,λ)(4) 设 A ( ω , b ) = min ⁡ w , b L ( ω , b , λ ) A(\omega,b) = \min_{w,b} L(\omega,b,\lambda) A(ω,b)=minw,b​L(ω,b,λ), B ( λ ) = max ⁡ λ L ( ω , b , λ ) B(\lambda) = \max_{\lambda} L(\omega,b,\lambda) B(λ)=maxλ​L(ω,b,λ), 同理可得： max ⁡ A ( ω , b ) ≤ min ⁡ B ( λ ) \max A(\omega,b) \leq \min B(\lambda) maxA(ω,b)≤minB(λ)即(3)得证。

要想等价用对偶问题求的话，我们还得使 min ⁡ w , b max ⁡ λ L ( ω , b , λ ) = max ⁡ λ min ⁡ w , b L ( ω , b , λ ) \min_{w,b} \max_{\lambda} L(\omega,b,\lambda) = \max_{\lambda} \min_{w,b} L(\omega,b,\lambda) w,bmin​λmax​L(ω,b,λ)=λmax​w,bmin​L(ω,b,λ)此即为强对偶关系。 （满足强对偶关系的充要条件是KKT条件，可以参考这篇知乎文章，这里我不想涉及太多的公式推导，否则将与文章本意相背，我们假设KKT条件已得，作为结论来用。同时，我在这篇文章里用几何方法比较简单直观的解释了对偶性，感兴趣的可以围观。）

可以先解出 min ⁡ w , b L ( ω , b , λ ) \min_{w,b}L(\omega,b,\lambda) minw,b​L(ω,b,λ), 分别对b和 ω \omega ω求偏导，这里计算比较繁琐，但是不难，通过代入可以求得 min ⁡ w , b L ( ω , b , λ ) = − 1 2 ∑ i = 1 N ∑ j = 1 N λ i λ j y i y j X i T X j + ∑ i = 1 N λ i (5) \min_{w,b}L(\omega,b,\lambda) = -\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\lambda_i\lambda_j y_i y_j X_i^TX_j + \sum_{i=1}^{N}\lambda_i \tag 5 w,bmin​L(ω,b,λ)=−21​i=1∑N​j=1∑N​λi​λj​yi​yj​XiT​Xj​+i=1∑N​λi​(5)

（source:https://zhuanlan.zhihu.com/p/26514613）

因此，优化问题又可等价为： max ⁡ λ min ⁡ w , b L ( ω , b , λ ) = max ⁡ λ − 1 2 ∑ i = 1 N ∑ j = 1 N λ i λ j y i y j X i T X j + ∑ i = 1 N λ i \max_{\lambda} \min_{w,b} L(\omega,b,\lambda) = \max_{\lambda} -\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\lambda_i\lambda_j y_i y_j X_i^TX_j + \sum_{i=1}^{N}\lambda_i λmax​w,bmin​L(ω,b,λ)=λmax​−21​i=1∑N​j=1∑N​λi​λj​yi​yj​XiT​Xj​+i=1∑N​λi​ s.t. λ i ≥ 0 , ∑ i = 1 N λ i y i = 0 (6) \text{s.t.} \lambda_i \geq 0 ,\sum_{i=1}^{N} \lambda_i y_i = 0 \tag 6 s.t.λi​≥0,i=1∑N​λi​yi​=0(6) 通过KKT条件，得到最优解 ω ∗ = ∑ i = 1 N λ i y i X i \omega^* = \sum_{i=1}^{N}\lambda_i y_i X_i ω∗=∑i=1N​λi​yi​Xi​和 b ∗ = y k − ∑ i = 1 N λ i y i X i T X k b^*= y_k - \sum_{i=1}^{N}\lambda_i y_i X_i^T X_k b∗=yk​−∑i=1N​λi​yi​XiT​Xk​, 注意这里的（Xk,yk）是一个支持向量（这里可以当作二维平面上等价思考理解）。 得到了 ω ∗ 和 b ∗ \omega^* \text{和}b^* ω∗和b∗,就找到了这个线性模型！即， f ( x ) = s i g n ( ω ∗ X + b ∗ ) f(x) = sign(\omega^*X + b^*) f(x)=sign(ω∗X+b∗) 解释一下，由KKT条件，只有 1 − y i ( ω T X i + b ) = 0 1-y_i(\omega^TX_i + b)=0 1−yi​(ωTXi​+b)=0时， λ i \lambda_i λi​才有值，所以由 ω ∗ = ∑ i = 1 N λ i y i X i \omega^* = \sum_{i=1}^{N}\lambda_i y_i X_i ω∗=∑i=1N​λi​yi​Xi​可得， ω ∗ \omega^* ω∗只是支持向量数据的线性叠加。关于以上还有不清楚的地方可以查看我推荐的文章，公式推导很清楚，但更重要的是理解和算法内核的把握。

你的鼓励是我创作的动力，如果你有收获，点个赞吧👍

我接下来还会陆续更新机器学习相关的学习笔记，补充这个系列。如果看到这里的话，说明你有认真看这篇文章，希望你能有所收获！最后，欢迎交流指正！

还有不明白的欢迎阅读其他文章： 通俗讲解支持向量机SVM（一）面试官：什么？线性模型你不会不清楚吧？ 通俗讲解支持向量机SVM（二）另辟蹊径！对偶性的几何解释 通俗讲解支持向量机SVM（三）SVM处理非线性问题及软间隔之引出 通俗讲解支持向量机SVM（四）用尽洪荒之力把核函数与核技巧讲得明明白白（精华篇）