以下链接是个人关于MVSNet(R-MVSNet)-多视角立体深度推导重建 所有见解，如有错误欢迎大家指出，我会第一时间纠正。有兴趣的朋友可以加微信：17575010159 相互讨论技术。若是帮助到了你什么，一定要记得点赞！因为这是对我最大的鼓励。 文末附带 \color{blue}{文末附带} 文末附带 公众号 − \color{blue}{公众号 -} 公众号− 海量资源。 \color{blue}{ 海量资源}。 海量资源。
3D点云重建0-00：MVSNet(R-MVSNet)–目录-史上最新无死角讲解：https://blog.csdn.net/weixin_43013761/article/details/102852209
代码引导改篇博客主要讲解的是Cost Volume Regularization以及soft_arg_min，但是Cost Volume Regularization没有什么好说的，其代码在mvsnet/train.py：
# filtered cost volume, size of (B, D, H, W, 1)=(?, 192, ?, ?, 1)
# 这里完成的是论文图示的Cost Volume Regularization操作，带有反卷积操作，对初始的cost_volume进行过滤
if is_master_gpu:
filtered_cost_volume_tower = RegNetUS0({'data': cost_volume}, is_training=True, reuse=False)
else:
filtered_cost_volume_tower = RegNetUS0({'data': cost_volume}, is_training=True, reuse=True)
# 进行维度压缩得到[B, D, H, W]
filtered_cost_volume = tf.squeeze(filtered_cost_volume_tower.get_output(), axis=-1)
对应论文图示： 
可以理解为，就是使用3D卷积，对Cost Volume进行了过滤，或者说把视觉差信息，转化为能求深度图的信息。主要的要点在于，怎么能让网络去学习这个转化过程，下面我们来看看吧。从RegNetUS0的输入和输出，以及改部分网络是看出来的，我们需要往后琢磨代码。
这里我先把代码贴出来，当然还是在mvsnet/model.py里面：
# depth map by softArgmin
with tf.name_scope('soft_arg_min'):
# probability volume by soft max
# tf.scalar_mul为标量与矢量相乘，这里乘以-1，等于加上了-号，
# 对3D立体的volume每个立体像素，都进行深度预测
# probability_volume[B, D, H, W],
# 这里的axis=1，也就是沿着D所在的轴，所有体素中存储的概率值相加为1
probability_volume = tf.nn.softmax(
tf.scalar_mul(-1, filtered_cost_volume), axis=1, name='prob_volume')
# depth image by soft argmin
# 获得probability_volume的形状[B, D, H, W]
volume_shape = tf.shape(probability_volume)
soft_2d = []
# 对每个样本进行处理
for i in range(FLAGS.batch_size):
# 对每个样本，根据depth_start[i], depth_end[i]的不同，但是划分成depth_num份
# tf.linspace使用，如tf.linspace(0,5,5)=[0,1,2,3,4]
soft_1d = tf.linspace(depth_start[i], depth_end[i], tf.cast(depth_num, tf.int32))
soft_2d.append(soft_1d)
# [b,d,1,1]
soft_2d = tf.reshape(tf.stack(soft_2d, axis=0), [volume_shape[0], volume_shape[1], 1, 1])
# [b,d,h,w]
soft_4d = tf.tile(soft_2d, [1, 1, volume_shape[2], volume_shape[3]])
#estimated_depth_map[b,h,w], 这个地方注意以下，filtered_cost_volume是乘了-1之后再计算概率的，为的就是深度的反转
# 把soft_4d现象成立体空间，因为前面是用tf.linspace生成，在D的方向存储的就是类似于1,2,3,4,5,6,7,..........这样的数据
# 假设r img的一个像素，经过tf.nn.softmax进行预测，落在三维空间深度为5的地方，那么是不是除了5的概率接近1，其他地方的概率低接近0
# （如果此时网络已经很好的收敛），5乘以一个接近1的数，他的值还是得5，其他的乘以一个接近0的数，那么结果接近为0
# 下面在D的方向axis=1进行求和，他们的值还是5，对吧。就是一个5加了很多个0
# 这样，我们就从二维空间先转到3维的概率空间，然后求和得到深度，有道理没？
estimated_depth_map = tf.reduce_sum(soft_4d * probability_volume, axis=1)
# [b,h,w,1]
estimated_depth_map = tf.expand_dims(estimated_depth_map, axis=3)
# 获得深度概率分布图
prob_map = get_propability_map(probability_volume, estimated_depth_map, depth_start, depth_interval)
return estimated_depth_map, prob_map#, filtered_depth_map, probability_volume
从上面我们可以看到，经过过滤得到的filtered_cost_volume，直接经过tf.nn.softmax进行分类处理，并且在这之前还乘以-1。得到的形状还是和filtered_cost_volume一样的，为[B, D, H, W]。注意的是tf.nn.softmax中的参数axis=1，表示的是按照深度来进行概率预算的。这个地方，比较就觉抽象，如下所示：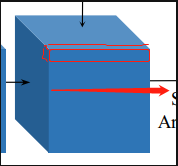 
也就是上面红色部分（我已经尽力了），红色部分的体素中保存的概率值相加为1，可以看到根据长宽不一样，这个probability_volume可以分成很多个类似红框的部分。
这样预测出来的东西是什么，其表示的是2维图像映射到3维空间后，他应该在处于哪个深度，那么在probability_volume，这个深度对应的位置，其存储的概率值会最大，那么可以想到D方向（箭头方向）其他的体素存储的概率值都接近0。
还要理解的就是estimated_depth_map = tf.reduce_sum(soft_4d * probability_volume, axis=1)，这个函数，其实就是计算的D方向的一个期望值。论文中的公式如下: D = ∑ d = d m i n d m a x d × P ( d ) D=\sum_{d=d_{min}}^{d_{max}}d \times P(d) D=d=dmin∑dmaxd×P(d)
到这里，我们已经知道了深度是怎么来的了，下面我们来看看概率图（Probability Map）。
Probability Map从上面我们可以找到：
......
# 获得深度概率分布图
prob_map = get_propability_map(probability_volume, estimated_depth_map, depth_start, depth_interval)
......
在讲解之前，我们来看看，概率的描述图： 
c中上面的图示，表示的是非离群点（概率都集中在一个深度），下面的表示的是离群点（概率都比较分散）。造成利群点的原因是什么？因为他是背景,那么为什么背景就会出现利群点？在论文中，也有提到过，那就是背景是不会进行反向传播和优化的（具体细后面讲解）。背景因为比较离散，4个值，当做一个值，有点类似于平滑的效果，我们先看看代码吧：
def get_propability_map(cv, depth_map, depth_start, depth_interval):
"""
get probability map from cost volume，
该函数的主要作用，可以这样理解，一个（4,）的滑动窗口，在cv（probability_volume）
滑动步伐为1，每滑动一次，都会把这四个像素存储的深度概率值都相加起来，
当作一个概率图prob_map的一个像素，这样能够去除异常点的干扰。带着这个
思路去分析，会比较简单
cv: probability_volume[B, D, H, W]，r img映射3维空间所处深度的概率值
depth_map: 推断出来的深度图[B,H,W,1]
depth_start :[b,]
"""
def _repeat_(x, num_repeats):
""" repeat each element num_repeats times """
x = tf.reshape(x, [-1])
ones = tf.ones((1, num_repeats), dtype='int32')
x = tf.reshape(x, shape=(-1,1))
x = tf.matmul(x, ones)
return tf.reshape(x, [-1])
# 获得推导出来深度图的形状，b，h，w
shape = tf.shape(depth_map)
batch_size = shape[0]
height = shape[1]
width = shape[2]
# 由概率立体获得深度
depth = tf.shape(cv)[1]
# byx coordinate, batched & flattened
# 把b,y,x的坐标一一列举出来
b_coordinates = tf.range(batch_size)
y_coordinates = tf.range(height)
x_coordinates = tf.range(width)
b_coordinates, y_coordinates, x_coordinates = tf.meshgrid(b_coordinates, y_coordinates, x_coordinates)
b_coordinates = _repeat_(b_coordinates, batch_size)
y_coordinates = _repeat_(y_coordinates, batch_size)
x_coordinates = _repeat_(x_coordinates, batch_size)
# d coordinate (floored and ceiled), batched & flattened
# 获得深度坐标，从零开始[？,]
# [b,h,w,1]-->[?,1],首先把深度图的数值，转化为depth_num（可以当作坐标使用，从0开始），然后再改变形状，注意该处为二维
d_coordinates = tf.reshape((depth_map - depth_start) / depth_interval, [-1])
# 把深度坐标限制再0与最大深度之间
d_coordinates_left0 = tf.clip_by_value(tf.cast(tf.floor(d_coordinates), 'int32'), 0, depth - 1)
# 首先把深度坐标都减去了1，然后又重新限定到0与最大深度之间
d_coordinates_left1 = tf.clip_by_value(d_coordinates_left0 - 1, 0, depth - 1)
# 把深度坐标限制再0与最大深度之间
d_coordinates1_right0 = tf.clip_by_value(tf.cast(tf.ceil(d_coordinates), 'int32'), 0, depth - 1)
# 首先把深度坐标都减去了+1，然后又重新限定到0与最大深度之间
d_coordinates1_right1 = tf.clip_by_value(d_coordinates1_right0 + 1, 0, depth - 1)
# voxel coordinates，对于每个深度像素，都获得周围一起4个像素的坐标
voxel_coordinates_left0 = tf.stack(
[b_coordinates, d_coordinates_left0, y_coordinates, x_coordinates], axis=1)
voxel_coordinates_left1 = tf.stack(
[b_coordinates, d_coordinates_left1, y_coordinates, x_coordinates], axis=1)
voxel_coordinates_right0 = tf.stack(
[b_coordinates, d_coordinates1_right0, y_coordinates, x_coordinates], axis=1)
voxel_coordinates_right1 = tf.stack(
[b_coordinates, d_coordinates1_right1, y_coordinates, x_coordinates], axis=1)
# get probability image by gathering and interpolation
# 通过深度像素坐标，获得4个深度像素的值
prob_map_left0 = tf.gather_nd(cv, voxel_coordinates_left0)
prob_map_left1 = tf.gather_nd(cv, voxel_coordinates_left1)
prob_map_right0 = tf.gather_nd(cv, voxel_coordinates_right0)
prob_map_right1 = tf.gather_nd(cv, voxel_coordinates_right1)
# 把四个深度方向（D方向的）像素全都相加起来，当作一个深度的值
prob_map = prob_map_left0 + prob_map_left1 + prob_map_right0 + prob_map_right1
prob_map = tf.reshape(prob_map, [batch_size, height, width, 1])
return prob_map
沿着深度方向，进行平滑之后，背景和前景就很容易的区分出来了。
到这里为止，我们已经讲解了论文如下部分： 
对应源码mvsnet/train.py中的：
depth_map, prob_map = inference(
images, cams, FLAGS.max_d, depth_start, depth_interval, is_master_gpu)
剩下的就是对深度图额提炼和loss函数的定义了，大家看到这里辛苦了，谢谢大家。如果觉得小伙子我讲得不错，要给个赞啊。
