以下链接是个人关于FSA-Net(头部姿态估算) 所有见解，如有错误欢迎大家指出，我会第一时间纠正。有兴趣的朋友可以加微信：a944284742相互讨论技术。若是帮助到了你什么，一定要记得点赞！因为这是对我最大的鼓励。 文末附带 \color{blue}{文末附带} 文末附带 公众号 − \color{blue}{公众号 -} 公众号− 海量资源。 \color{blue}{ 海量资源}。 海量资源。
姿态估计1-00：FSA-Net(头部姿态估算)-目录-史上最新无死角讲解
前言通过前面的博客，我们已经了解了整个网络的构建过程，从该小结开始，我们就开始要琢磨其细节的实现，对于ssr_G_model模型的实现，太简单简单了，就是获得K=3个
h
×
w
×
c
h\times w\times c
h×w×c的特征图，即lib/FSANET_model.py中BaseFSANet类的ssr_G_model_build模型的实现。在pre-trained文件中，可以找到他的很多可视化，如pre-trained/fsanet_capsule_3_16_2_21_5/ssr_G_model.png：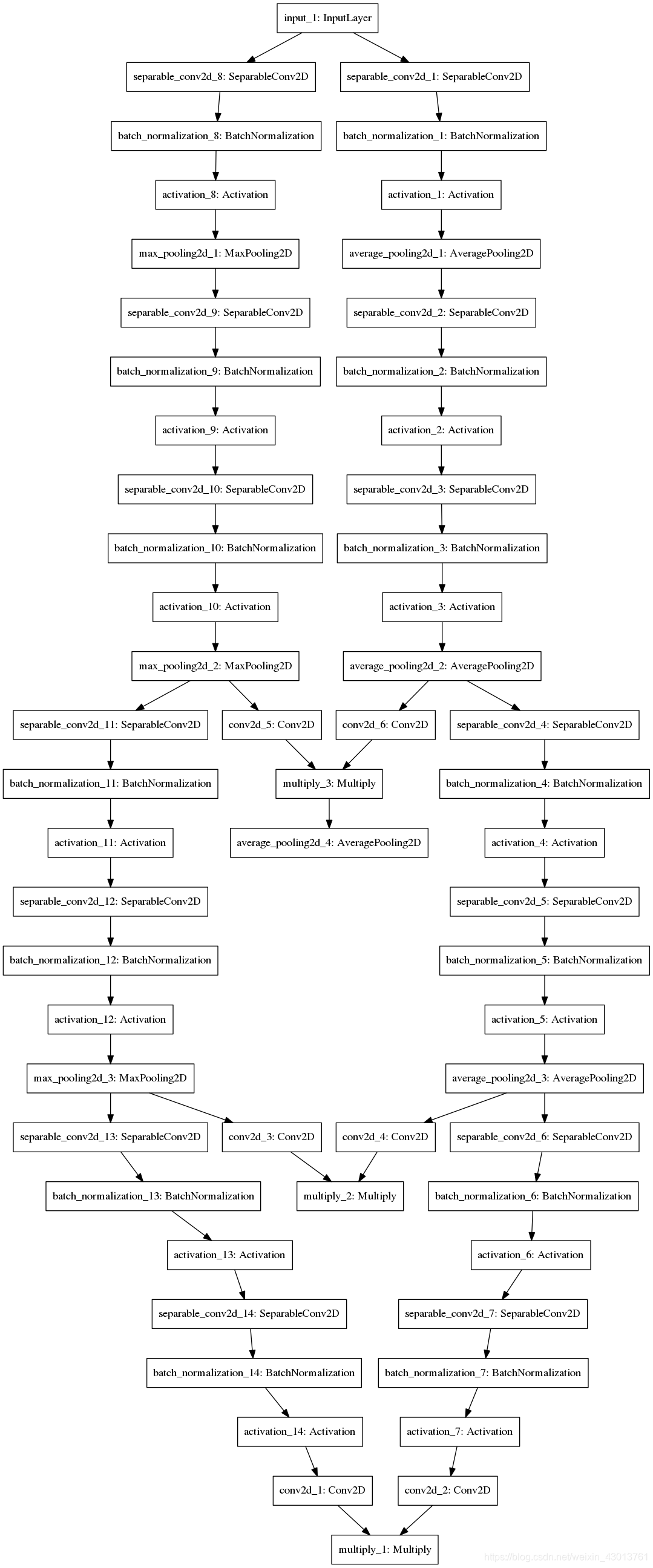 
我觉得，看这个图，比我讲解肯定更加明确。那么下面我们就来看看Fine-grained structure mapping 以及Scoring function的实现。
对于其实现，在代码lib/FSANET_model.py中，先找到def call(self):函数，实现如下：
# 根据参数，确定是否构建论文中Scoring模型,输入三个[b,8,8,64],得到一个[b,3*7,64]
if self.is_noS_model:
# 三个[b,8,8,64]输入, 链接到一起成为[b,192,64]输出
ssr_S_model = self.ssr_noS_model_build()
没有使用Scoring function，那么这就是最基本的Fine-grained structure mapping结构了，从论文知道，该结构的主要作用是为了更好的，对空间细节特征的提取，其把每个特征图进行了分组处理，先看看ssr_noS_model_build到底做了什么：
def ssr_noS_model_build(self, **kwargs):
# 输入为3个[8,8,64]的特征图
input_s1_preS = Input((self.map_xy_size,self.map_xy_size,64))
input_s2_preS = Input((self.map_xy_size,self.map_xy_size,64))
input_s3_preS = Input((self.map_xy_size,self.map_xy_size,64))
# 进行形状改变，变成3个[64,64]的特征向量
primcaps_s1 = Reshape((self.map_xy_size*self.map_xy_size,64))(input_s1_preS)
primcaps_s2 = Reshape((self.map_xy_size*self.map_xy_size,64))(input_s2_preS)
primcaps_s3 = Reshape((self.map_xy_size*self.map_xy_size,64))(input_s3_preS)
# 连接之后的形状为[b,192,64]
primcaps = Concatenate(axis=1)([primcaps_s1,primcaps_s2,primcaps_s3])
return Model(inputs=[input_s1_preS, input_s2_preS, input_s3_preS],outputs=primcaps, name='ssr_S_model')
有点尴尬奥，和我想的似乎不一样，就是把K个特征图全部扁平了，然后连接到一起。3个[8,8,64]的特征图变成了一个[b,192,64]的特征图。没关系，我们继续往下看。如我我们使用了Scoring function，其又是怎样的一个实现过程呢？
在_call_函数中，找到如下代码：
else:
# 如果构建Scoring模型，其有两种方式，分别为使用1x1的卷积，或者通过方差计算
# 三个[b, 8, 8, 64]输入， num_primcaps参数为192,
# 输出[b,21,64]
ssr_S_model = self.ssr_S_model_build(num_primcaps=self.num_primcaps,m_dim=self.m_dim)
然后我们查看ssr_S_model_build的实现过程：
def ssr_S_model_build(self, num_primcaps, m_dim):
# input_s1_preS与input_s2_preS及input_s3_preS都为[b,8,8,64]
input_s1_preS = Input((self.map_xy_size,self.map_xy_size,64))
input_s2_preS = Input((self.map_xy_size,self.map_xy_size,64))
input_s3_preS = Input((self.map_xy_size,self.map_xy_size,64))
# 根据参数构建合适的Scoring function模型
feat_S_model = self.ssr_feat_S_model_build(m_dim)
# 得到SR_matrix_sx[b,5,192], feat_sx_preS[b,64]
# SR_matrix_s1，SR_matrix_s2，SR_matrix_s3表示论文中的MK，从论文中，我们可以知道该矩阵不共用的
# feat_sx_preS表示的是论文中的attention map Ak
SR_matrix_s1,feat_s1_preS = feat_S_model(input_s1_preS)
SR_matrix_s2,feat_s2_preS = feat_S_model(input_s2_preS)
SR_matrix_s3,feat_s3_preS = feat_S_model(input_s3_preS)
# 把3个attention map 连接起来得到一个feat_pre_concat，也就是论文中的A，形状为[b,192]
feat_pre_concat = Concatenate()([feat_s1_preS,feat_s2_preS,feat_s3_preS])
# 根据整体的feat_pre_concat，获得论文中的C矩阵，这个矩阵是共用的，论文中有提到
SL_matrix = Dense(int(num_primcaps/3)*m_dim,activation='sigmoid')(feat_pre_concat)
# 形状为[b,7,5], num_primcaps=7
SL_matrix = Reshape((int(num_primcaps/3),m_dim))(SL_matrix)
# 进行矩阵相乘，使用 C和 K个MK矩阵相乘，得到SK，即论文中的SK=C*MK
# [b,7,5][b,5,192]=[b,7,192]
S_matrix_s1 = MatrixMultiplyLayer(name="S_matrix_s1")([SL_matrix,SR_matrix_s1])
S_matrix_s2 = MatrixMultiplyLayer(name='S_matrix_s2')([SL_matrix,SR_matrix_s2])
S_matrix_s3 = MatrixMultiplyLayer(name='S_matrix_s3')([SL_matrix,SR_matrix_s3])
# 对SK[b,7,192]每个192维度(每一行)的特征向量进行正则化,
# Very important!!! Without this training won't converge.
# norm_S_s1 = Lambda(lambda x: K.tile(K.sum(x,axis=-1,keepdims=True),(1,1,64)))(S_matrix_s1)
# [b,7,192]-->[b,7,1]-->[b,7,64],注意啊，这里只进行了192个维度平方和的计算，
# 也就是说，只是都分母进行的计算，后面每个元素还要除以这个分母
norm_S_s1 = MatrixNormLayer(tile_count=64)(S_matrix_s1)
norm_S_s2 = MatrixNormLayer(tile_count=64)(S_matrix_s2)
norm_S_s3 = MatrixNormLayer(tile_count=64)(S_matrix_s3)
# 输入的特征进行形状改变[b,8,8,64]-->[b,64,64]
feat_s1_pre = Reshape((self.map_xy_size*self.map_xy_size,64))(input_s1_preS)
feat_s2_pre = Reshape((self.map_xy_size*self.map_xy_size,64))(input_s2_preS)
feat_s3_pre = Reshape((self.map_xy_size*self.map_xy_size,64))(input_s3_preS)
# 3个[b,64,64]链接成[b,192,64]的特征向量
feat_pre_concat = Concatenate(axis=1)([feat_s1_pre, feat_s2_pre, feat_s3_pre])
# Warining: don't use keras's 'K.dot'. It is very weird when high dimension is used.
# https://github.com/keras-team/keras/issues/9779
# Make sure 'tf.matmul' is used
# primcaps = Lambda(lambda x: tf.matmul(x[0],x[1])/x[2])([S_matrix,feat_pre_concat, norm_S])
# 上面有注释，就是(S_matrix_s1* feat_pre_concat)/norm_S_s1
# ([b,7,192] [b,192,64])/[b,7,64] = [b,7,64]
# 这里除了矩阵相乘，还完成了归一化操作
primcaps_s1 = PrimCapsLayer()([S_matrix_s1,feat_pre_concat, norm_S_s1])
primcaps_s2 = PrimCapsLayer()([S_matrix_s2,feat_pre_concat, norm_S_s2])
primcaps_s3 = PrimCapsLayer()([S_matrix_s3,feat_pre_concat, norm_S_s3])
# 3[b,7,64]个链接起来变成[b,21,64]
primcaps = Concatenate(axis=1)([primcaps_s1,primcaps_s2,primcaps_s3])
return Model(inputs=[input_s1_preS, input_s2_preS, input_s3_preS],outputs=primcaps, name='ssr_S_model')
通过代码注释，我们可以知道，该函数主要完成了以下过程：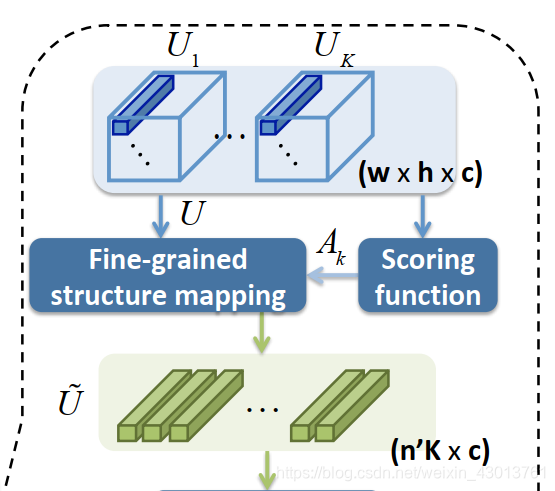 
其中Scoring function使用函数：
feat_S_model = self.ssr_feat_S_model_build(m_dim)
封装起来，我们后续进行详细讲解。下面我把代码中的变量和论文中的参数对应起来：
feat_pre_concat= U U U, [192,64] = [n,c]
SR_matrix_sx = M k M_k Mk, [5,192=8x8x3] = [m,n]
SL_matrix = C C C, [7,5] = [n’,m]
primcaps_sx= U ~ k \tilde U_k U~k, [7,64] = [n’,c], 注意 U ~ \tilde U U~表示把 U ~ 1 \tilde U_1 U~1， U ~ 2 \tilde U_2 U~2， U ~ k \tilde U_k U~k链接起来，为源码中的primcaps参数。
这些参数都能在下图中找到：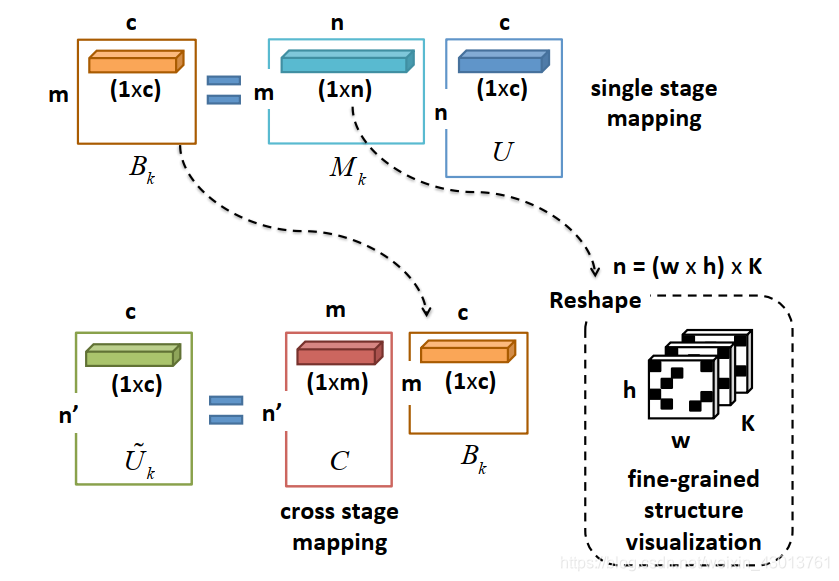 
总的来说，ssr_S_model_build函数实现了如下部分：在这里插入代码片 1.把输入的K个
U
K
U_K
UK扁平成
U
U
U 2.根据
U
U
U获得attention map 3.结合attention map生成
M
k
M_k
Mk与
C
C
C 4.利用
M
k
M_k
Mk与
C
C
C，对
U
U
U进行分组，或者说进行空间细节的提取，得到
U
~
k
\tilde U_k
U~k
前面已经对ssr_S_model_build函数进行了很详细的的讲解，也理清楚了Fine-grained structure mapping的整个过程，但是我们忽略了其中重要的一个函数，即：
# 根据参数构建合适的Scoring function模型
feat_S_model = self.ssr_feat_S_model_build(m_dim)
该函数注释如下：
# 根据参数构建论文中对应的Scoring
def ssr_feat_S_model_build(self, m_dim):
input_preS = Input((self.map_xy_size,self.map_xy_size,64))
# 如果使用方差计算Scoring,
if self.is_varS_model:
# [b, 8, 8, 1]
feat_preS = MomentsLayer()(input_preS)
# 如果使用[1,1]的卷积计算Scoring
else:
# [b, 8, 8, 1]
feat_preS = Conv2D(1,(1,1),padding='same',activation='sigmoid')(input_preS)
# 把feat_preS铺平,为[b,64]
feat_preS = Reshape((-1,))(feat_preS)
# SR_matrix[b,192x5=960], 该处理解为全连接层之后使用sigmoid函数
SR_matrix = Dense(m_dim*(self.map_xy_size*self.map_xy_size*3),activation='sigmoid')(feat_preS)
# [b,5,192]
SR_matrix = Reshape((m_dim,(self.map_xy_size*self.map_xy_size*3)))(SR_matrix)
return Model(inputs=input_preS,outputs=[SR_matrix,feat_preS],name='feat_S_model')
其实现的过程也非常的简单，首先对输入的特征图 U k [ 8 × 8 × 64 ] U_k[8\times8\times 64] Uk[8×8×64]进行方差计算，或者卷积，得到的feat_preS都为[8,8,1]，也就是论文中的 A K A_K AK,然后通过 A K A_K AK经过全链接获得SR_matrix，也就是论文中的 M k M_k Mk矩阵。
结语好了，到这里，这篇博客就结束了。是不是，在我的分析下，源码变得十分的清晰，都和论文对应了起来。哈哈，不吹逼了，下篇博客我们依旧不见不散。点赞啊，大帅哥，超级大帅哥，一定要点赞哈
