原文地址：【Unity-学习-003】导弹，跟踪弹怎么玩？ 可能要翻墙
直线轨迹导弹预判可用于塔防类游戏的直线道路，当导弹速度较目标慢时，需要预判才能追上。
注释的做法将转动速度调慢可以作为敌人限制转动速度的跟踪导弹，方便玩家走位。
下面一些地方排版比较难看 但是原理写的很细致清楚。Demo也能运行
最近在玩一款飞行射击游戏，时常驾驶着自己的飞机在枪林弹雨中穿行，然后就快要通过关卡的时候，我奋力的击杀，却依然顶不住敌军猛烈的攻势。在敌机如蛇皮般的走位中，忍着快要抓狂的心情努力的把着鼠标，但我的准星却仍然无法瞄准到敌人。想想都很气！如果这时候，能在飞机上发射出跟踪弹~~~~~~，贼舒服！
首先梳理一下，一般导弹有以下两种模式。
①跟踪发射之后尾随目标飞行，直到击中目标，BOOM！ ②预判 发射之后，判断目标的飞行方向，然后前去拦截，直到击中目标，BOOM！
首先我们来说说跟踪。
一般想到的就是 transform.LookAt(Vector3 worldPos) 方法。这个方法可以让该 transform 看向这个 worldPos ，此时如果把 worldPos 改成需要追踪的目标的位置，放在 Update 中每帧调用，那么就会让 transform 在自己的生命周期中，始终看向目标。
代码如下：
using UnityEngine;
public class Rocket : MonoBehaviour
{
public Transform target; //跟踪目标
public GameObject FX; //爆炸特效
public float moveSpeed; //移动速度
public float rotateSpeed ; //旋转速度
private void Update()
{
if (target != null) //判断当前是否有跟踪目标 如果有的话 执行 以下跟踪逻辑
{
transform.LookAt(target);
// Vector3 tempDirV = target.position - transform.position; //计算出正确的转向
// Quaternion rightDirQ = Quaternion.LookRotation(tempDirV); //将转向 转化为 四元数
// transform.rotation = Quaternion.Lerp(transform.rotation, rightDirQ, rotateSpeed); //利用四元数插值方法 将方向赋给 transform.rotation
}
transform.position += transform.forward * moveSpeed * Time.deltaTime; //向前移动
}
//当 有物体进入到 自己的触发器时 调用一次
private void OnTriggerEnter(Collider other)
{
GameObject tempFX = Instantiate(FX, transform.position, transform.rotation); //生成一个爆炸特效 并给予位置和旋转信息
Destroy(gameObject); //销毁自己
Destroy(tempFX, 1); //等待 1秒 销毁刚才 创建生成的爆炸特效
}
}
然后来说预判。
先来想想预判的逻辑是怎样的。所谓预判，就是拦截。我们得知道的数据：
target 移动方向，移动速度 self 移动速度
其中移动方向，有两种情况。因为逻辑是一帧一帧的运行，所以我们选取碰撞的前一帧为基准。
同向 反向
在target的后方发生碰撞 在target的脸前发生碰撞
下图是同向轨迹示意图
下图是反向轨迹示意图
同向 反向相同处
其中 向量 Vab = target.position - rocket.position。
L3 = Vab.magnitude。
计算出 ∠α = Vector3.angle(Vab ，target.移动方向)。
L2 = Mathf.Cos(∠α * Mathf.Deg2Rad) * L3 。
L1 = Mathf.Sin(∠α * Mathf.Deg2Rad) * L3 。
根据勾股定理：a{2}+b{2}=c^{2} 有下面的推导
同向 反向 L1^2 + (L2+ Vb*t)^2 = (Va * t)^2 L1^2+(L2 - Vb*t)^2 = (Va * t)^2 (Vb ^ 2 - Va ^ 2) * t ^ 2+(2 * L2 * Va) * t+(L1 ^ 2+L2 ^ 2) = 0 (Vb ^ 2-Va ^ 2) * t ^ 2-(2 * L2 * Va) * t+(L1 ^ 2+L2 ^ 2) = 0看的出是一元二次三项式，解 at^{2}+bt+c =0
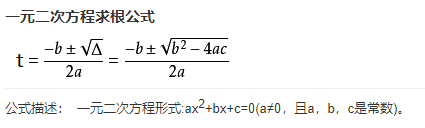这样就解出来时间 t 。在 t 秒后两者相遇。
从而依据 t ，Vb ，target.position ，计算出 Boom点（C点）。也就是当前的碰撞点。
其中主要的代码逻辑如下：
Vector3 AB= target.position - transform.position;
float angle = Vector3.Angle(AB, targetDir); //获取角度
float L1 = Mathf.Sin(angle * Mathf
