GAMES101作业5-从头到尾理解代码&Whitted光线追踪

Whitted Ray-Tracing Whitted光线追踪

What

Why

How

1 发射主射线primary ray

实现步骤

（1）定义相机

（2）计算primary主射线的方向

Renderer.cpp->render()

2 射线交互

3 获得相交对象的属性

光线与球求交&光线与面求交

sphere.hpp求交

global.hpp求根函数

回到trace()求交

std::optional

4 递归光线跟踪

reflective 表面材质类似mirror

反射光线方向

考虑误差-偏移值epsilon

Renderer.cpp->reflect()

Renderer.cpp->castRay()->case REFLECTION

transparent 透明

折射光线方向

Renderer.cpp->refract()

Renderer.cpp->castRay()->case REFLECTION_AND_REFRACTION

菲涅尔效应

菲涅尔方程

Special Case 特殊情况

Renderer.cpp->fresnel()

diffuse/glossy 具有漫反射特性且表面不透明

Renderer.cpp->castRay()->default:

Whitted Ray-Tracing Whitted光线追踪 What

Whitted-style光线追踪是由特纳惠特首次提出的，利用折射定律和菲涅尔方程来计算光线与反射或透明物体表面相交时的反射和折射光线的方向，遵循光线路径来获得相交对象的颜色。

Why

知道了Whitted光线追踪是什么之后，接下来需要思考的是：为什么需要光线追踪呢？这是因为我们知道的Blinn-Phong光照模型无法处理全局效果！这一点在games101课上P8-GAMES101-现代计算机图形学入门-闫令琪老师就提到过：

1.强调Phong shading is local -Phong模型是局部的；NO Shadow - 不考虑阴影；

2.介绍环境光照时，假设环境光加上了一个常数颜色，并解释这样的作法其实是”fake“的，牵扯到全局光照，后续课程就会涉及到。

再回到内容：到底什么是局部光照和全局光照？需要引入新的两个点：直接光照direct illumination和间接光照indirect illumination。

局部光照 local illumination

在这之前先说说直接光照(direct illumination)：通常，点光源和平行光源这种理想光源发出光线到物体表面产生的光照我们叫做直接光照。

只考虑直接光照的光照效果我们叫做局部光照。

全局光照 global illumination

再说说间接光照 (indirect illumination)：维基是这样解释的：Indirect Illumination is effectively the illumination within a scene that does not come from an actual light source, and effectively refers to reflected light.在真实世界中，不仅要考虑理想光源带来的光照效果，还有区域光的存在，光线在玻璃、镜子等物体表面之间还会发生弹射，这种现象也是组成光照的重要部分，我们称为间接光照。

考虑间接光照的光照效果我们成为全局光照。

How

已经知道是什么和为什么了，下面要谈谈如何实现Whitted Ray-Tracing。

Whitted光线追踪实现步骤

参考Whitted光线追踪实现_0小龙虾0的博客可以将其分为四个模块步骤：

创造主射线primary ray：从摄像机的每个像素发射一条主射线，sending rays to the scene;
投射射线交互：根据发射的主射线和场景对象进行交互；
获得相交对象的属性：如果主射线与物体表面有交点，则需要得到交点表面属性（法线、材质特性等）；
递归光线跟踪：根据物体表面特性，判断是否要发射二次射线secondary ray（包括折射射线and反射射线），需要递归发射的两条新射线，进行跟踪计算。

1 发射主射线primary ray

sending rays into the scene.

参考：Ray Tracing in One Weekend

参考描述：the ray tracer sends rays through pixels and computes the color seen in the direction of those rays.

实现步骤（1）定义相机

把相机中心（eye）定在(0,0,0)，Y方向向上，X向右，遵循右手定则->screen为-Z方向。

...
    //Image
    std::vector framebuffer(scene.width * scene.height);
    //deg2rad() 度数->弧度
    float scale = std::tan(deg2rad(scene.fov * 0.5f));
    //aspect_radio=width/height
    float imageAspectRatio = scene.width / (float)scene.height;
    // Use this variable as the eye position to start your rays.
    //eye(相机中心)定为(0,0,0)
    Vector3f eye_pos(0);
...

（2）计算primary主射线的方向

参考：Whitted光线追踪实现_0小龙虾0的博客

需要清楚的是，这个方向是从相机出发(0,0,0)->像素中心(x,y,z)，把pixel从栅格空间->世界空间，其实就相当于做了一次逆向光栅化！

还记得光栅化rastering吗？

Step.1 —— world space -> screen space

先将world space场景中的点通过投影变换 -> screen space

一个标准cube里，这个标准空间叫做NDC space

Step.2 —— screen space -> NDC space（归一化设备坐标）

这个步骤就是缩放成

$\left [ -1,1 \right ]^{2}$ （这里的1并不是像素的尺寸1，而是一个unit）

Step.3 —— NDC space -> raster space

把标准的cube按照raster成image的需求，从

$\left [ -1,1 \right ]^{2}$

按照image的尺寸拉伸成

$\left [ 0,ImageWidth \right ]\times \left [ 0,ImageHeight \right ]$

这里要逆向光栅化，就反着来！

1.首先实现raster space -> NDC space

已知像素坐标，求NDC坐标

$PixelNDC_{x}=\frac{(Pixel_{x}+0.5)}{ImageWidth}$

$PixelNDC_{y}=\frac{(Pixel_{y}+0.5)}{ImageHeight}$

注意，这里的(x,y)并不是表示一个像素的中心，而是表示一个像素的左下角，我们希望光线穿过像素中心，而像素是边长为1的正方形，因此需要+0.5。但是加上之后NDC空间的坐标范围会变成

$\left [ 0,1 \right ]$

进行矫正：(0,0) -> (-1,-1) ，(1,0) ->(1,-1)，(1,1) ->(1,1)，(0,1) ->(-1,1)，带入得到

$PixelScreen_{x}=2*PixelNDC_{x}-1$

$PixelScreen_{y}=1-2*PixelNDC_{y}$

2.将压缩的x轴复原

可事实是，我们的Screen往往宽高比不是1：1，往往有这样一个值来记录宽高比

$ImageAspectRatio=\frac{ImageWidth}{ImageHeight}$

参考图来自：Whitted光线追踪实现_0小龙虾0的博客

如上图所示，以尺寸为7X5为例：由NDC[0,1]得到的[-1,1]的Screen space，为了储存下5X7=35个像素，像素在会被压缩，因为一般width>height的，因此都是在x方向被压缩，我们需要给他再变回正方形，就要给x轴坐标乘上宽高比，y轴保持不变。

3.视口变换

目前这一步其实我们太搞懂，先截图放上参考的说法，之后再琢磨。

现在搞懂了，这个截图里的公式应该有一点错误，它所指的PixelScreen(x,y)坐标应该代表的是上述流程中的Pixel(x,y)坐标。

Renderer.cpp->render()

//发射主射线primary ray
//sending rays into the scence
void Renderer::Render(const Scene& scene)
{
    //Image
    std::vector framebuffer(scene.width * scene.height);
    //deg2rad() 度数->弧度
    float scale = std::tan(deg2rad(scene.fov * 0.5f));
    //aspect_radio=width/height
    float imageAspectRatio = scene.width / (float)scene.height;

    // Use this variable as the eye position to start your rays.
    //eye(相机中心)定为(0,0,0)
    Vector3f eye_pos(0);
    //遍历每个像素
    int m = 0;
    for (int j = 0; j < scene.height; ++j)
    {
        for (int i = 0; i < scene.width; ++i)
        {
            // generate primary ray direction
            //计算主射线方向
            float x;
            float y;
            // TODO: Find the x and y positions of the current pixel to get the direction
            // height->j->第j行->对应坐标为y
            // width->i->第i列->对应坐标为y 
            
            //我们这里先定义一个虚拟的窗口 -> camera
            // camera         
            x = 2 * scale * imageAspectRatio / scene.width * (i + 0.5) - scale * imageAspectRatio;
            y = -2 * scale / scene.height * (j + 0.5) + scale;
            //定义dir
            //这里直接让摄像机在世界坐标朝向(0,0,-1)构建screen space，就可以省去screen space ->world space的转换
            Vector3f dir = Vector3f(x, y, -1); // Don't forget to normalize this direction!
            dir = normalize(dir);
            framebuffer[m++] = castRay(eye_pos, dir, scene, 0);
        }
        UpdateProgress(j / (float)scene.height);
    }

    // save framebuffer to file
    FILE* fp = fopen("binary.ppm", "wb");
    (void)fprintf(fp, "P6\n%d %d\n255\n", scene.width, scene.height);
    for (auto i = 0; i < scene.height * scene.width; ++i) {
        static unsigned char color[3];
        color[0] = (char)(255 * clamp(0, 1, framebuffer[i].x));
        color[1] = (char)(255 * clamp(0, 1, framebuffer[i].y));
        color[2] = (char)(255 * clamp(0, 1, framebuffer[i].z));
        fwrite(color, 1, 3, fp);
    }
    fclose(fp);    
}

2 射线交互

这个交互就是games101作业5框架里的castRay()函数，可以放在第4步一起说。

3 获得相交对象的属性光线与球求交&光线与面求交

这部分主要是trace()&getSurfaceProperties()两个函数在实现。

trace() —— 进行射线求交计算；

getSurfaceProperties() —— 获得物体表面属性。

这里的intersect()是在Sphere.hpp里定义的一个bool函数，可以结合其来一起看。

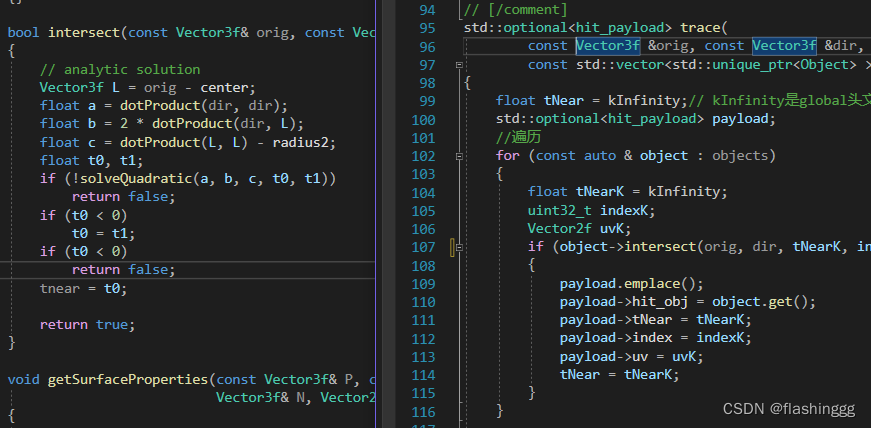
可以看到主要是根据课上讲的来写的步骤：

sphere.hpp求交

//判断ray与物体表面是否相交，输入光源点-orig，入射ray方向-dir，tnear-深度值
    //线与圆求交
    bool intersect(const Vector3f& orig, const Vector3f& dir, float& tnear, uint32_t&, Vector2f&) const override
    {
        // analytic solution
        Vector3f L = orig - center;
        float a = dotProduct(dir, dir);
        float b = 2 * dotProduct(dir, L);
        float c = dotProduct(L, L) - radius2;
        float t0, t1;
        //!solve ，如果return true则if不成立；false则成立，return false
        if (!solveQuadratic(a, b, c, t0, t1)) //global.hpp定义的函数，用于判断是否有根
            return false;
        if (t0 < 0)
            t0 = t1;
        if (t0 < 0)//t0被赋值成ti后再判断一次，如果两个解都＜0，则交点是无效的
            return false;
        tnear = t0;//tnear=有效解的最小值

        return true;
    }

global.hpp求根函数

inline bool solveQuadratic(const float& a, const float& b, const float& c, float& x0, float& x1)
{
    float discr = b * b - 4 * a * c;
    if (discr < 0)
        return false;
    else if (discr == 0)
        x0 = x1 = -0.5 * b / a;//一个根
    else
    {
        float q = (b > 0) ? -0.5 * (b + sqrt(discr)) : -0.5 * (b - sqrt(discr));
        x0 = q / a;
        x1 = c / q;
    }
    if (x0 > x1)
        std::swap(x0, x1);//根一大一小，取最近的点，因此要swap位置保证x0也就是t0是最小的
    return true;
}

回到trace()求交

std::optional trace( //hit_payload是Renderer.hpp中定义的一个struct
        const Vector3f &orig, const Vector3f &dir,
        const std::vector &objects)
{
    float tNear = kInfinity;// kInfinity是global头文件定义的，返回float型数的最大值
    std::optional payload;
    //遍历
    for (const auto & object : objects)
    {
        float tNearK = kInfinity;
        uint32_t indexK;
        Vector2f uvK;
        //tNear是经过遍历后目前这条光线遇见物体交点最近的位置
        //如果当前计算的tNearK>tNear,说明当前的object被挡住了
        //所以就算与光线有焦点也不需要进行储存
        if (object->intersect(orig, dir, tNearK, indexK, uvK) && tNearK < tNear)
        {
            payload.emplace();
            payload->hit_obj = object.get(); //hit_obj做的操作会反应在智能指针object指向的对象上
            payload->tNear = tNearK;//tnearK=最近一点的根
            payload->index = indexK;//
            payload->uv = uvK;
            tNear = tNearK;//上面的只是改变了payload的tNear，这里赋值的是trace的tNear，用于进行下一个object的tNear 、*访问值value() payload.value()
 访问值，如果有则返回，如果没有提交异常
 value_or() payload.value_or()
 访问值，如果有则返回如果没有返回给到的值 swap()交换值emplace()payload.emplace() 分配一个()里的新值 
参考：std::optional - cppreference.com 
最后，关于具体的求交计算光线跟踪的几种常见求交运算_0小龙虾0的博客-CSDN博客_求交运算写的非常清晰，可以参考。 
4 递归光线跟踪 
根据物体的材质属性的反射/折射情况，可以将着色方法分为以下几种： 
（1）reflective mirror类型的 
（2）transparent 透明的 
（3）diffuse/glossy 具有漫反射特性且表面是光滑不透明的 
 
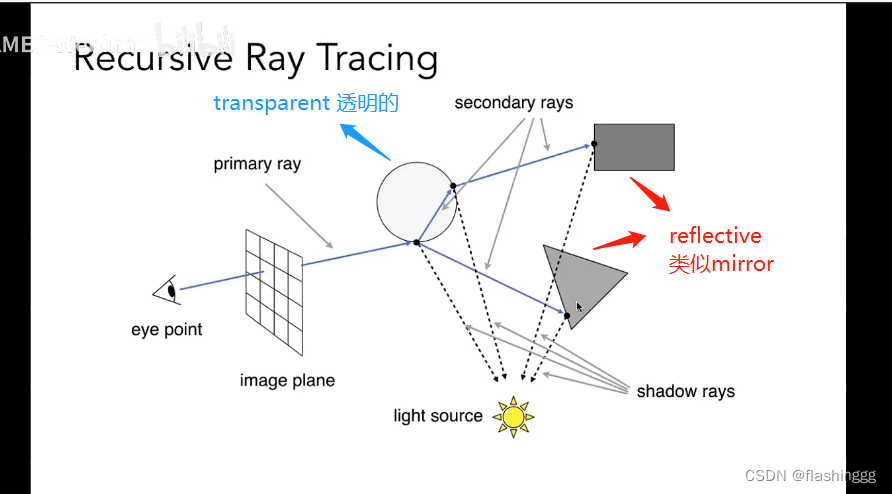
下面对每个情况如何实现光线追踪进行详细的阐述 
reflective 表面材质类似mirror 
在相交处发射出一条反射光线就行（跟踪一条反射的射线）。这个反射的射线方向可以通过反射定律得到，即“三线共面，两线分居，两角相等”。 
反射光线方向 
 
  
 
其中，向量B是入射光线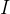在法线方向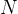的负方向上的投影：(注意这里的向量都是单位向量) 
 
 
考虑误差-偏移值epsilon 
参考自：Whitted光线追踪实现_0小龙虾0的博客-CSDN博客 
因为计算机精度的问题，直接使用起点产生噪声值，如下图： 
 
 由于精度损失，通过计算得到的相交点坐标往往不会正中理论上的点位置，而是会向外或者向内一点点，为了解决这个问题采用一个小小的偏移值epsilon来解决这个问题（体现在后续代码上） 
 
Renderer.cpp->reflect() 
// Compute reflection direction
Vector3f reflect(const Vector3f &I, const Vector3f &N)
{
    return I - 2 * dotProduct(I, N) * N;
} 
Renderer.cpp->castRay()->case REFLECTION 
...
            //mirror
            case REFLECTION:
            {
                //菲涅耳定律->得到反射光线占比kr
                float kr = fresnel(dir, N, payload->hit_obj->ior);
                //计算反射射线方向
                Vector3f reflectionDirection = reflect(dir, N);
                //由于计算问题会出现误差，如果点在面内就向N方向偏移；如果点在面外就向-N方向偏移
                Vector3f reflectionRayOrig = (dotProduct(reflectionDirection, N) < 0) ?
                                             hitPoint + N * scene.epsilon ://epsilon是定义的一个浮点数的bias,epsilon=0.00001
                                             hitPoint - N * scene.epsilon;
                //接着递归使用castRay()把计算的反射起点Orig和方向Dir带入，并*反射光线占比kr，继续跟踪折射和反射射线
                //这里的depth+1意思是发生了一次反射，有最大次数限制->maxDepth
                hitColor = castRay(reflectionRayOrig, reflectionDirection, scene, depth + 1) * kr;
                break;
            }
... 
transparent 透明 
 在相交处发射两条射线：一条反射射线；一条折射射线。反射射线方向由上面的反射定律得到，折射射线方向由斯奈尔定理（Snell’s Law）通过推导得到。 
折射光线方向 
这里要用到Snell's laws斯内尔定律 
 
——表示入射角和折射角与二者介质的折射率的关系 
根据入射光线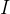向量和法向量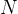推导折射光线向量。 
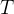推导过程可以看参考的两篇文章，得到的折射向量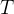的公式为 
 
其中， 
 
 
 
 参考： 
折射向量的推导__gamer的博客-CSDN博客 
 折射向量推导 - 知乎 
Renderer.cpp->refract() 
 
 //计算折射向量
Vector3f refract(const Vector3f &I, const Vector3f &N, const float &ior)
{
    //dotProduct点积（来自vector.hpp定义的
    //clamp是个区间限定函数，在这里其实就是把cosi的值限定在了[-1,1]之间
    float cosi = clamp(-1, 1, dotProduct(I, N));
    float etai = 1, etat = ior;//1为空气折射率，ior为介质的折射率
    Vector3f n = N;
    //如果入射光从介质1(etai)->介质2(etat)，则夹角>90°；
    //如果入射光从介质2->介质1，则夹角castRay()->case REFLECTION_AND_REFRACTION 
...
           //透明
            case REFLECTION_AND_REFRACTION:
            {
                //反射方向
                Vector3f reflectionDirection = normalize(reflect(dir, N));
                //折射方向
                Vector3f refractionDirection = normalize(refract(dir, N, payload->hit_obj->ior));
                //由于计算问题会出现误差，如果点在面内就向N方向偏移；如果点在面外就向-N方向偏移
                //epsilon是定义的一个浮点数的bias,epsilon=0.00001
                Vector3f reflectionRayOrig = (dotProduct(reflectionDirection, N) < 0) ?
                                             hitPoint - N * scene.epsilon :
                                             hitPoint + N * scene.epsilon;
                Vector3f refractionRayOrig = (dotProduct(refractionDirection, N) < 0) ?
                                             hitPoint - N * scene.epsilon :
                                             hitPoint + N * scene.epsilon;
                //两条光线射线又开始作为入射光线，递归使用castRay()追踪
                //这里的depth+1意思是发生了一次反射，有最大次数限制->maxDepth
                Vector3f reflectionColor = castRay(reflectionRayOrig, reflectionDirection, scene, depth + 1);
                Vector3f refractionColor = castRay(refractionRayOrig, refractionDirection, scene, depth + 1);
                //计算反射光线占比
                float kr = fresnel(dir, N, payload->hit_obj->ior);
                //计算着色值
                hitColor = reflectionColor * kr + refractionColor * (1 - kr);
                break;
            }
...
            
还需要确定反射和折射光线的占比，这里就用到了菲涅尔反射定律（Fresnel Reflection） 
菲涅尔效应 
简单来说，离表面越近看到更多的折射光（视线与表面接近垂直），越远则看到更多的反射光（视线与表面几乎平行），学过高中物理或者大物的都有印象，其实就是光线反射与折射。通俗一点讲：入射角越大，反射的光越多。而用Unity手册里的菲涅尔效应的解释来说，“现实世界中物体的一个重要视觉提示与它们在掠射角下如何变得更具反射性有关”，这就是菲涅尔效应。 
 
从图（来自Unity手册）可以看出，随着物体材质变得光滑，观察者掠射角可见的菲涅尔效应更加明显。 
 
那么到底是反射光更强还是折射光更强，需要比较辐射度量学里Radiance（在games101ray tracing3有讲）的大小。渲染时需要考虑这一点进去，渲染出来的才会更加真实，这就需要一个公式，描述不同入射光下反射光与折射光所占比例，这就是菲涅尔方程。 
菲涅尔方程 
 借用参考资料的描述： 
当光线碰撞到一个表面的时候，菲涅尔方程会根据观察角度告诉我们被反射的光线所占的百分比。利用这个反射比率和能量守恒原则，我们可以直接得出光线被折射的部分以及光线剩余的能量。将其应用在BRDF当中，我们就可以更加精准的计算出渲染方程中的值。 
具体推导可以看我列出的参考文章，这里直接列出菲涅尔方程的表达式： 
 
其中： 
 
  
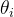——入射光与法线的夹角 ，——折射光与法线的夹角，——入射介质折射率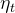，——折射介质折射率。 
Special Case 特殊情况 
题目中给的Special cases —— Total internal reflection  
当在密度较高的介质中传播的光撞击密度较低的介质（即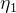>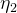）的表面时，超过称为临界角的特定入射角，所有光都被反射并且 。这种现象被称为全内反射，发生在入射角处。斯内尔定律预测折射角的正弦将exceed unity（而实际上，for all real  ,）。因此就有了后面定义的： 
if (sint >= 1) {
        return 1;
} 
特殊情况其实还有： 
Normal incidence —— 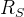，和没区别 
 Brewster's angle 
参考： 
菲涅耳效应 - Unity 手册 
菲涅尔方程（Fresnel Equation） - 知乎 (zhihu.com) 
Fresnel equations - Wikipedia 
Renderer.cpp->fresnel() 
//计算菲涅尔方程
float fresnel(const Vector3f &I, const Vector3f &N, const float &ior)
{
    float cosi = clamp(-1, 1, dotProduct(I, N));
    float etai = 1, etat = ior;
    if (cosi > 0) {  std::swap(etai, etat); }
    // Compute sini using Snell's law 即：sin比等于折射率反比
    float sint = etai / etat * sqrtf(std::max(0.f, 1 - cosi * cosi));
    // Total internal reflection，全反射
    if (sint >= 1) {
        return 1;
    }
    else {
        //cos²+sin²=1
        float cost = sqrtf(std::max(0.f, 1 - sint * sint));
        cosi = fabsf(cosi);
        float Rs = ((etat * cosi) - (etai * cost)) / ((etat * cosi) + (etai * cost));
        float Rp = ((etai * cosi) - (etat * cost)) / ((etai * cosi) + (etat * cost));
        return (Rs * Rs + Rp * Rp) / 2;
    }
    // As a consequence of the conservation of energy, transmittance is given by:
    // kt = 1 - kr;
    //意思->由能量守恒，透光率的值为：kt=1-kr
    //光穿透物体表面会发生：折射refraction、次表面散射subsurface和半透明透射transmission
    //kt-transmission , kr-refraction ,这里似乎没考虑ks
    //次表面散射一般发生在半透明材质：皮肤、玉、蜡、大理石、牛奶等
} 
diffuse/glossy 具有漫反射特性且表面不透明 
用Phong-shading模型来计算相交对象的颜色；
同时还需要判断场景中的点是否在阴影中，需要从相交对象向场景中的光源投射一个阴影射线（shadow ray）来判断这个相交对象是否在阴影中
经典的whited-style光线追踪遇到漫反射表面会直接利用blinn-phong模型计算颜色值返回，而不再递归下去。 
 Renderer.cpp->castRay()->default: 
...
            default:
            {
                //进行phong模型
                //lightAmt - 环境光
                //specularcolor代表三个通道内高光的分量
                Vector3f lightAmt = 0, specularColor = 0;
                //进行一个矫正
                Vector3f shadowPointOrig = (dotProduct(dir, N) < 0) ?
                                           hitPoint + N * scene.epsilon :
                                           hitPoint - N * scene.epsilon;
                // [comment]
                // Loop over all lights in the scene and sum their contribution up
                // We also apply the lambert cosine law-这个定理就是那个cos的由来
                // [/comment]
                // Phong光照模型
                //遍历场景中所有的光源点
                //Light(const Vector3f& p, const Vector3f& i) position & intensity(I/r²)
                for (auto& light : scene.get_lights()) {
                    Vector3f lightDir = light->position - hitPoint;
                    // square of the distance between hitPoint and the light
                    float lightDistance2 = dotProduct(lightDir, lightDir);
                    lightDir = normalize(lightDir);
                    float LdotN = std::max(0.f, dotProduct(lightDir, N));

                    //shadow ray - 环境光
                    // 一条shadow ray从hitpoint出发，以lightdir为方向，如果shadow_res=true ->说明被遮挡了
                    auto shadow_res = trace(shadowPointOrig, lightDir, scene.get_objects());
                    // 如果返回的tnear shadow ray被路径上的某一个表面遮挡了，到达不了light，因此说明hitpoint在这条ray的阴影里
                    bool inShadow = shadow_res && (shadow_res->tNear * shadow_res->tNear < lightDistance2);
                    //hitpoint在阴影里->inshadow=true->lightAmt=0(无环境光)
                    //hitpoint不在阴影里->inshaow=false->lightAmt+=I/r²*max(0, cos)
                    lightAmt += inShadow ? 0 : light->intensity * LdotN;
                    //这里求反射ray方向，用到reflect(),仔细看这个函数里的lightdir定义的是从光源出发，因此这里lightDir要取-lightDir
                    //得到反射ray方向为后面求高光做准备
                    Vector3f reflectionDirection = reflect(-lightDir, N);

                    //高光 v无限接近r ->  dir就是v ; reflectiondirection就是r 这里可以参考之前老师讲phong模型的式子
                    specularColor += powf(std::max(0.f, -dotProduct(reflectionDirection, dir)),
                        payload->hit_obj->specularExponent) * light->intensity;
                }
                //diffusecolor - 三个通道内光线的diffuse分量，是vector3f类型
                // kd ks 是 float类型
                //hitColor = lightAmt*diffusecolor*kd+specularcolor*ks
                hitColor = lightAmt * payload->hit_obj->evalDiffuseColor(st) * payload->hit_obj->Kd + specularColor * payload->hit_obj->Ks;
                break;
            }
        }
    }

    return hitColor;//如果以上if没成立，则无交点，返回背景色
}
...
 
结果展示

GAMES101作业5-从头到尾理解代码&Whitted光线追踪

[ 申请 ]友情链接：