这个数字的存在其实是很「自然」的一件事情……
1 / 多少妃子得不到皇帝的宠幸？首先，不扯任何公式，更不扯极限的概念，让我们穿越回古代，看一个在当时应该是很「自然」的事情：皇帝宠幸妃子。
问题很简单：
假设皇帝在宫中一共有1000位妃子，每天 完全随机地抽选一位妃子来宠幸，之后妃子安然无恙地回去，如此以往重复大概3年（1000天），那么，最终有多少位妃子能够得到宠幸、又有多少得不到宠幸呢？
答案是：如果每一天确实都完全随机地选妃子，那么1000位妃子里面，最终将会有大约632位被选中过，而剩下的368位妃子则一次都没有被宠幸过。
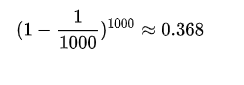
上面这个简单的例子看似和 e 没有任何关联，但是请把这个比例倒一下：
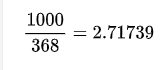
好像和 e 很接近啊？是巧合吗？
别急，如果这位皇帝有一万名妃子，以相同方式重复一万天（大概27年），那么理论上会有3679位妃子最终得不到宠幸；如果再多一点，十万，那么就是36788……
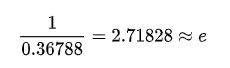
换句话说，上面这个「皇帝宠幸妃子」的问题，理论上会有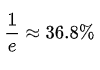 
比例的妃子最终得不到皇帝的宠幸。
一开始我对上面这件事将信将疑：真的会有这么多的妃子没被抽中吗？直到我打开RStudio，在R语言里面写了几行简单的代码来模拟上面这个过程，才发现确实如此：
set.seed(1)
sample = sample(1:10^6, replace=TRUE) # replace = 有放回取样
p = 1 - sum(unique(sample) %in% 1:10^6)/10^6
1/p结果发现，p（未被宠幸的妃子比例）是0.367975，而1/p是2.718。
这就是统计学中的「重抽样」技术（Bootstrap Sampling）：从数量为N的样本中「有放回地」随机抽取出一个「数量同样为N」的样本，那么理论上来说，原来的N个个体中大约会有36.8%的个体不会被抽中。
如果一定要写出一个公式：
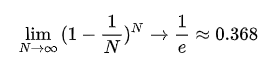
Bootstrap技术本身已经在自然科学、社会科学的很多领域得到了广泛应用。而上述这个特殊的问题，其实也已经应用于机器学习：在“随机森林（random forest）”算法中，每一棵决策树在建立的时候，所需要的数据并非原始数据（N），而是通过bootstrap方法有放回地抽取的具有相同样本量N的样本，其中不重复的个案大约是63.2% * N，而剩下的36.8% * N的样本则被称为“出包/袋外数据（out-of-bag data, OOB）”。这样一来，很自然地，重抽样得到的样本可以作为“训练集”来训练机器学习模型，而36.8%的OOB数据（相当于那些“未被宠幸的妃子”）可以作为“测试集”来验证模型的预测性能。
实际上，我们还可以用一种“更自然”的方式来描述这个问题，而不涉及任何具体数字，这样就回应了评论区关于此问题情境是否足够“自然”的疑问（e.g.,
皇帝在宫中有成百上千的妃子，派人每天【完全随机地】抽选一位妃子来宠幸（或者条件允许的话，每个时辰一位也可以喔 [坏笑.emoji] ），之后妃子安然无恙地回去。若干年后，皇帝“目测”那么多的妃子应该都【宠幸完一遍】了吧？但愚昧的皇帝并不知道，其实还是有很多妃子没有得到宠幸呢。问这个比例是多少？
依然是那个公式：
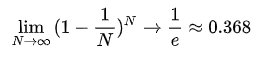
【思考题】受到评论区
的启发，我们还可以思考一个不太一样的情形：如果仍然是1000位妃子，但是每次随机抽2人、共抽500次呢？
我们使用R语言进行模拟：
set.seed(1)
sample = c()
for(day in 1:500) sample = c(sample, sample(1:1000, 2))
p = 1 - sum(unique(sample) %in% 1:1000)/1000
p答案仍然非常接近36.8%。
类似地，每次随机抽4人、共抽250次（需满足“抽样总和等于总人数”、“每次抽的数量远小于总人数”），也会得到十分相近的答案。
链接：https://www.zhihu.com/question/20296247/answer/708727036
