摄像机模型与标定

摄像机模型与标定

• 视觉开始于检测大千世界的自然光线。一个简单而有用的解释视网膜成像的模型便是针孔摄像机模型。

• 针孔是一堵想象中的墙（中心有一个微型小孔），光线只能从这个开口中通过，而其余的都被墙所阻挡。在这里，我们将从一个针孔相机模型开始，处理基本几何中的投影射线。遗憾的是，真实的针孔由于不能为快速曝光收集足够的光线。因此它不是一个得到图像的好方法。——此处解释了为什么需要使用透镜的问题。 然而，这种利用透镜得到更多的光线的缺点是，不仅使我们背离了所使用的简单针孔几何模型，而且引入来自透镜的畸变。

• 这里我们将学习如何利用摄像机标定，来矫正（数学方式）因使用透镜而给针孔模型带来的主要偏差。摄像机标定的重要性还在于它是摄像机测量与真实三维世界测量的联系桥梁，场景不仅仅是三维的，也是用物理单位度量的空间。因此，摄像机的自然单位（像素）和物理世界的单位（米）的关系对三维场景的重构至关重要。

• 摄像机标定的过程既给出摄像机几何模型，也给出透镜的畸变模型。这两个模型定义了摄像机的内参数。

摄像机模型

• 摄像机内参数： 4个内参数：

  fx,fy,cx,cy
  5个畸变系数：
  k1,k2,p1,p2,k3
  这个五个畸变参数，前两个径向参数首先出现，然后是两个切向参数，最好是第三个径向参数，因为第三个镜像畸变参数是OpenCV发展中新加入的成员，因此放在最后。主要是用于广角（鱼眼）镜头。 注：相机内参数矩阵为：
  ⎡⎣⎢fx000fy0cxcy0⎤⎦⎥

• 摄像机外参数： 旋转向量（大小为1x3的矢量或旋转矩阵3x3）和平移向量（Tx，Ty，Tz）。

这里我们讲解一下旋转向量：（参考我之前的一篇博文《罗德里格斯》） 旋转向量是旋转矩阵紧凑的变现形式，旋转向量为1x3的行矢量。

上述公式中r就是旋转向量： 1)旋转向量的方向是旋转轴； 2)旋转向量的模为围绕旋转轴旋转的角度。通过上面的公式三，我们可以求解出旋转矩阵R。同样的已知旋转矩阵，我们也可以通过下面的公式求解得到旋转向量：

相机模型如下图 对于图11-1所示，f是摄像机焦距，Z是摄像机到物体的距离，X是物体长度，x是图像平面上的物体图像。其数值可以通过相似三角形-x/f=X/Z得到，或

光轴与图像平面的交点被称为 主点。对于图像11-2：平面到投影中心的距离是f。 注意：： 你也许认为主点即等于成像仪的中心，但这意味着某些人拿着镊子和胶水要把摄像机里面的成像仪以微米级别的精度安装。实际上，芯片的中心通常不在光轴上。我们因此引入两个新的参数: 对可能的偏移（对光轴而言）进行建模。这样物理世界中的点Q，其坐标为（X,Y,Z），以某些偏移的方式投影为点： 采用理想针孔，我们有了一个对视觉中的三维几何有用的模型。但请记住，由于只有很少量的光线通过针孔，这导致是实际情况下因曝光不足使得图像生成得很慢。 对要快速生成图像得摄像机而言，必须利用大面积且弯曲的透镜，让足够多的光线能够收敛聚焦到投影点上。 透镜畸变

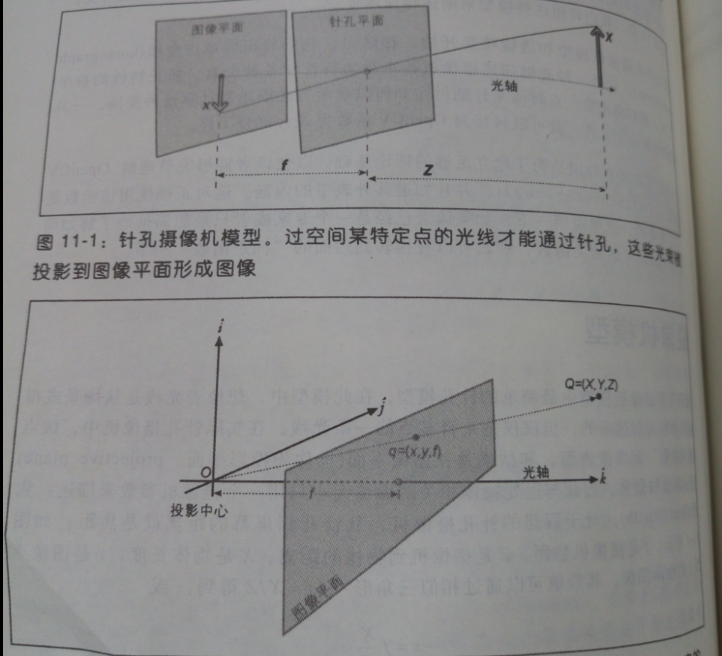
理论上讲是可能定义一种透镜而不引入任何畸变的。然而现实世界没有完美的透镜。因为制作一个“球形”透镜比制作一个数学上理想的透镜更容易。而且从机械方面也很难把透镜和成像仪保持平行。这里我们主要描述两种主要的透镜畸变并且为它们建模。径向畸变来自于透镜形状，而切向畸变则来自于整个摄像机的组装过程。 对于径向畸变。实际摄像机的透镜总是在成像仪的边缘产生显著的畸变。这个头痛的现象来源于“筒形”或“鱼眼”影响。对于径向畸变，成像仪中心（光学中心）的畸变为0，随着向边缘移动，畸变越来越严重。实际情况中，这种畸变比较小，而且可以用r=0位置周围的泰勒级数展开的前几项来定量描述。对便宜的网络摄像机，我们通常使用前两项，其中第一项通常为k1,而第二项为k2。对畸变很大的摄像机，比如鱼眼透镜，我们可以使用第三径向畸变项k3。通常，成像仪某点的径向位置按下式进行调节：

这里（x,y）是畸变点在成像仪上的原始位置，（Xcorrected,Ycorrected）是校正后的新位置。

第二大常用畸变是切向畸变。这种畸变是由于透镜制造上的缺陷使得透镜本身与图像平面不平行而产生的。

切向畸变可以用两个额外参数p1和p2来描述，如下：

标定

利用OpenCV来计算内参数矩阵和畸变向量的过程。

旋转和平移

在三维空间中，旋转矩阵可以分解为绕各自坐标轴的二维旋转，其中旋转轴线的度量保持不变。如果依次绕x,y,z轴旋转,那么总的旋转矩阵R是三个矩阵的乘积，其中：

旋转矩阵R的特性是它的逆阵就是它的转置阵（我们只需转回来）。因此有：

其中，I是对角元素为1，其余为0的单位矩阵。

平移向量用来表示怎样将一个坐标系的原点移动到另一个坐标系的原点，或者说，平移向量是第一个坐标原点与第二个坐标系原点的偏移量。因此，从以目标中心为原点的坐标系移动到以摄像机中心为原点的另一个坐标系，相应的平移向量为T=目标原点-摄像机原点。那么有图11-7，点在世界坐标系中的坐标Po到在摄像机坐标系中的坐标Pc:

结合上面计算Pc的公式以及摄像机内参数校正，我们构造出OpenCV所能解决的基本方程式。这些方程的解将是我们所寻找的摄像机标定参数。 棋盘

在《Learning OpenCV》书中，使用的是棋盘格来作标定板。可是在文章《Accurate Camera Calibration using Iterative Refinement of Control Points》中指出，同心圆的特征优于角点。所以在实验中，我们都是选择了同心圆作为特征点。

单应性

在计算机视觉中，平面的单应性被定义为从一个平面到另一个平面的投影映射。 因此一个二维平面上的点映射到摄像机成像仪上的映射就是平面单应性的例子。如果对点Q到成像仪上的点q的映射使用齐次坐标，这种映射可以用矩阵相乘的方式表示。若有以下定义：

则可以将单应性简单表示为：

这里引入参数s，它是一个任意尺度比例（目的是使得单应性被定义到该尺度比例）。通常根据习惯放在H的外面。 摄像机标定

最后我们为摄像机内参数和畸变参数进行摄像机标定。

棋盘角点个数和参数个数

首先回顾我们的未知因素，即标定过程求解究竟需要多少参数？在OpenCV里，我们有4个内参数（fx,fy,cx,cy）和5个畸变参数——三个径向（k1,k2,k3）和两个切向（P1，P2）。内参数直接与棋盘所在空间的3D几何相关（即外参数），而畸变参数则与点集如何畸变的2D集合相关。因此我们要分别处理两大类参数。为求解5个畸变参数（为了增加鲁棒性自然也可以有更多参数），需要已知模式的三个角点所产生的6组信息（在理论上）是所有需要解决的5个畸变参数（当然，可以利用更多的参数以达到鲁棒性）。因此，在内参数计算中，可以利用一个棋盘的6个不同棋盘视场，接下来考虑外参数。对外参数，我们需要知道棋盘的位置。对棋盘的6个不同视场图像，需要三个旋转参数和三个平移参数，因为在每幅图像中棋盘是移动的。总而言之，在每个视场中，我们必须计算4个内参数和6个外参数。

假设有N个角点和K个棋盘图像（不同位置），需要多少视场图像和角点才能提供足够的约束来求解所有这些参数？

• K个棋盘图形提供2NK个约束（乘以2是因为每个点都由x和y两个坐标值组成的）

• 忽略每次的畸变参数，我们有4个内参数和6K个外参数（因为我们需要在每K个视场中的找到棋盘位置的6个参数）

• 有解的前提是2NK>=6K+4（或者等价地，（N-3）K>=2）

似乎当N=5且K=1时成立。且慢，对于我们，K（图像个数）必须大于1。

矫正

标定摄像机通常是想做两件事，一个是矫正畸变效应，另一个是根据获得的图像重构三维场景。首先，我们先解决第一个任务。

OpenCV提供一个直接使用的校正算法，即输入原始图像和由函数cvCalibrateCamera2()得到的畸变系数，生成矫正后的图像。我们既可以通过一次性通过函数cvUndistort2()使用该算法完成所有事项，也可以通过一对函数cvInitUndistortMap()和cvRemap()来更有效率地处理此事，这通常适合视频或者从同一摄像机中得到多个图像的应用。 注： **“矫正”和“校正”的关系： “矫正”是在数学上去掉透镜畸变，而“校正”是数学上将图像排列整齐。**

一次完成标定

当使用算法时，在连续的捕获之间想要充分地改变棋盘的视角，否则求解标定参数的点集会是病态矩阵（非满秩），其结果是要么得到一个坏解，要么干脆无解。