你知道索引的底层数据结构是什么吗？
mysql为什么用B+树而不用红黑树？
mysql为什么用B+树而不用B树？ … … 这样一些问题经常出现来mysql的面试中，mysql中两个比较重要的概念就是锁与索引，而mysql的行锁本身就是通过锁定索引来实现的，所以理解索引的底层原理十分必要。
那么今天，我们从mysql索引的底层数据结构出发，带大家学习mysql的底层原理
1. 什么是索引？首先我们要来复习一下索引的概念，什么是索引？
官方对于索引的定义是帮助mysql高效获取数据的数据结构。就像我们把一张表看作一本书的话，索引就是我们的目录。所以索引的本质呢是数据结构，将指定数据按照一定的结构顺序存放。
索引如何实现高效的查找数据呢？想象一下，我现在有一堆杂乱无章的数据：2，4，5，7，2，1，6
你如何找到快速的找出5的位置呢？按照我们全表查询的思维我们需要从左往右，将数据一一遍历一遍，找出所有值为5的位置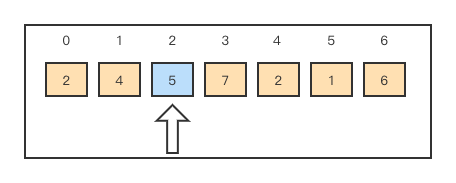 
这样的查询速度，肯定达不到我们高效查询的效果。就像你想从字典从查询某个字的话，难道你会一页一页的翻阅查找吗？
想想我们是怎么做的？根据拼音、根据偏旁部首等等一些特征来归类查询的。其实就是将其索引按照一定的排序规则进行排序，因为有序了，那么我们的查找速度就能提高了。
2. 数据结构的选择既然知道要排序了，那么下一步我们就要选择适当的数据结构了，这里可能需要大家具有一定的数据结构知识，常用的可排序的数据结构有哪些？
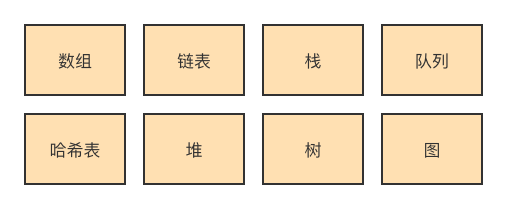
其中最能提高查询效率的就是hash表和树
因此mysql中正是利用了这两种数据结构来作为索引的底层结构支撑。
但我们需要注意的是，hash表因为将key作为hash code后存储，随机查询能力极强，但是不具备排序的能力，因为已经被hash一遍了，丢失了原本的数值。所以一般用于等值查询，而不能用于范围查询与排序
在mysql中只有memory存储引擎支持hash表。而innodb和myisam都是使用的B+树，hash表的结构也比较简单，所以我们今天来重点讲解B+树结构，以及mysql是如何一步步进化到B+树的结构的。
3. 树的演变 3.1 二叉搜索树 BST其实谈到树结构，我们首先想要的是较为简单的二叉树，但因为要具有排序的能力，于是引入了二叉搜索树（Binary Search Tree,BST），这里我就不再对各种树结构的基本概念进行讲解了，如果还没有掌握这块知识的同学可以先学习树的各种结构
我们利用数据结构可视化网站来使用二叉搜索树来将上述的数据重新排序。同时也非常推荐大家使用这个网站来学习数据结构
原数据：2，4，5，7，2，1，6
我们可以看到这样的结构，查询1时，只需要2步就能找到，大大提高了查询效率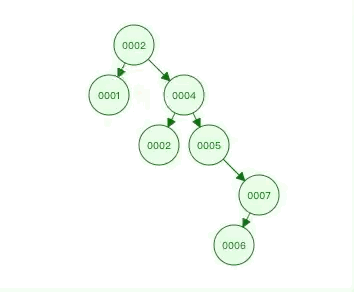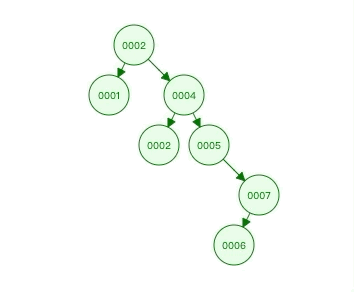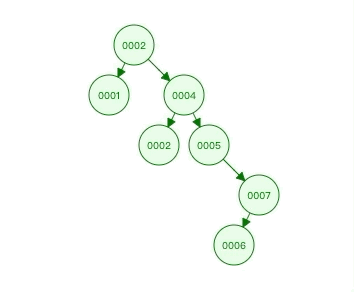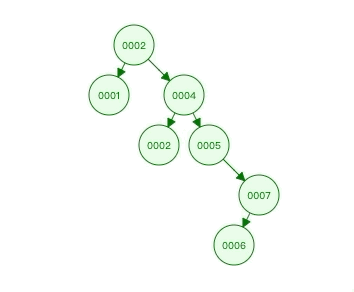 
但这样的结构有一个非常致命的问题，当我们的数据本身就是有序时，就会退化为链表结构，其查询速度又变成了全表查询的速度
于是我们引入了二叉平衡树(Balanced binary search trees,AVL)，他会通过旋转自动调整树的结构，也就是说他会自动保证树结构的平衡，而不会出现二叉搜索树的问题。当然旋转操作也是要消耗性能的，是通过牺牲更新数据时的性能来换取查询数据时的性能，但是这样的牺牲显然是值得的。
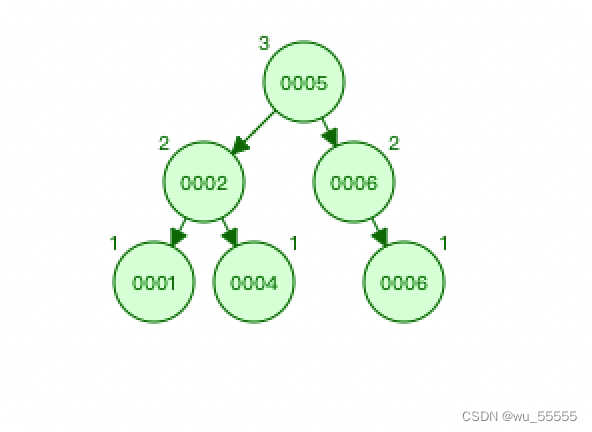那么二叉平衡树就能解决问题了吗？很遗憾并不能， 二叉平衡树有一个限制：最短子树和最高子树之间的高度差不能超过1
怎么理解这句话呢？我们再插入一个1和5，大家会发现我们的最高子树是2、1、1，高度是3，而最低子树有3个，高度都是2，其相差都不会超过1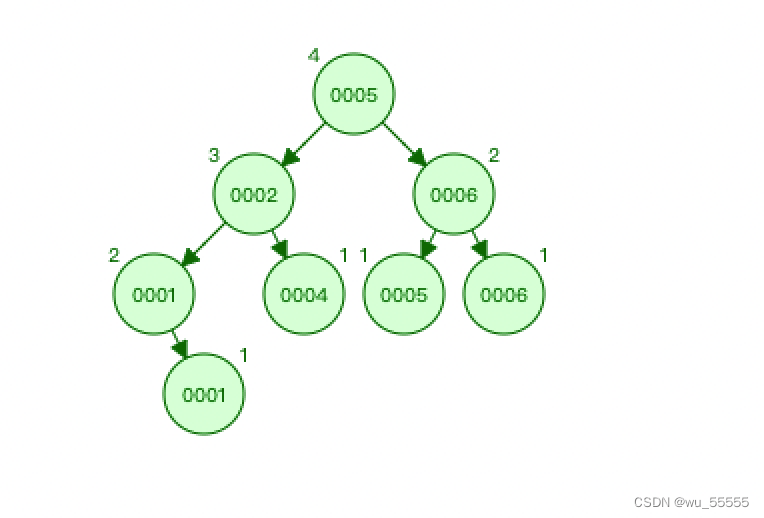 
这样的一个规定导致一个非常严重的问题，当我们的数据越来越多时，因为子树相差不能超过1，那最高的子树高度以增加，最低的子树高度也要跟着增加，也就导致整个树的高度越来越高
树的高度增加会带来什么问题？我们对于数据的查找，实际上是和高度相关的，高度越高，当我们要查询底下的数据时，消耗的时间就越久，比如上图所示，我们要查询1时，我们要从5->2->1->1才能查询完
并且数据的存储还有一个问题，数据在磁盘中存储如何物理空间是挨在一起的，那么其查询速度就快，如何不是挨在一起的查询速度就慢，这也正是我们上章中举的村头村尾的例子。
所以也就意味着，树越高需要查询时需要消耗的IO就多，查询速度就慢。因此AVL也不能满足了
有同学看到这里，可能会说，既然最低子树和最高子树高度差限制为1导致了这个问题，那么你把高度差限制取消掉不就好了吗？
想象一下我们把高度差限制取消掉，AVL怎么判断是否要旋转来调整树结构呢？不旋转不就又退回到BST了吗？
那既然高度差限制不能取消，你调大一点嘛～ 对咯！这就是我们要讲的下一种树的思路
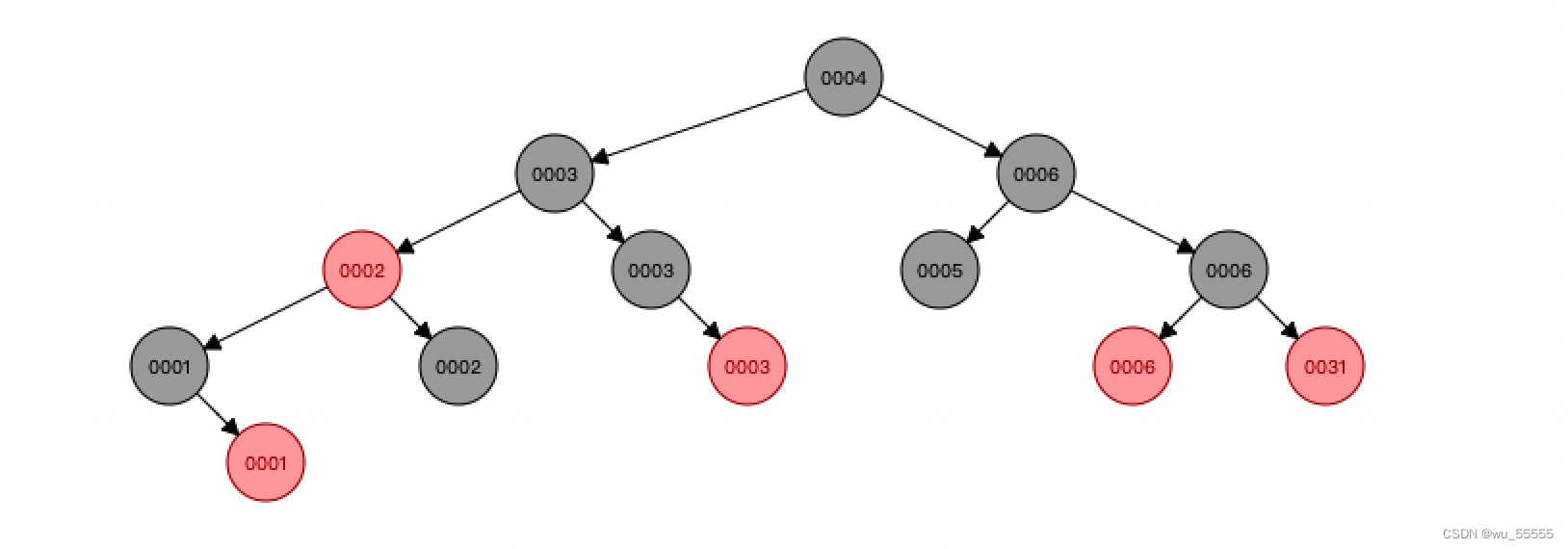
3.3 红黑树红黑树(Red-Black Trees)通过左旋和右旋来调整树高的平衡，并且加入了变色的行为，要求根节点为黑色，其他节点都是红色，也因此得名，通过加入颜色值，作为二叉树平衡度的检查标准，只要插入节点的颜色满足要求，最短树高和最长树高之差不会相差太远。
并且红黑树将树高差限制放宽了，只要最高子树的树高不超过最矮子树的树高的2倍即可
同时红黑树在jdk1.8中也被作为HashMap的底层数据结构，似乎一切都在朝着美好的一面发展。
但你以为这样就结束了吗？
NO! 生活往往会在我们放松警惕的时候给我们沉重打击。随着业务量的持续增加，数据量变得越来越多，红黑树的树高还是会不可避免的越来越高，即使高度差拓展到了2倍，可还是不够～
为什么会这样呢？大家不要忽略一个最重要的因素，红黑树也依然是二叉树，二叉！它只有两个分支，即使再旋转，它也只有两个分支，只要数据量达到一定地步，树的高度不可避免的还是要增加。
有的同学可能就会疑惑了，那为什么HashMap可以用红黑树而mysql里就不能用了呢？
这就是使用场景的不同了，mysql作为持久性的数据库存储，基于磁盘来实现，而HashMap可能作为代码运算或者本地缓存，并不作数据的持久化存储，基于内存来实现，其场景就已经限制磁盘存储的量一定比内存存储的量要大的多得多。
那解决办法是什么呢？
很简单，很粗暴，就是增加分支数！
3.4 B树B树是有序多叉树，每个节点中能够存储的数据变多了，同时每层的节点数也增加了
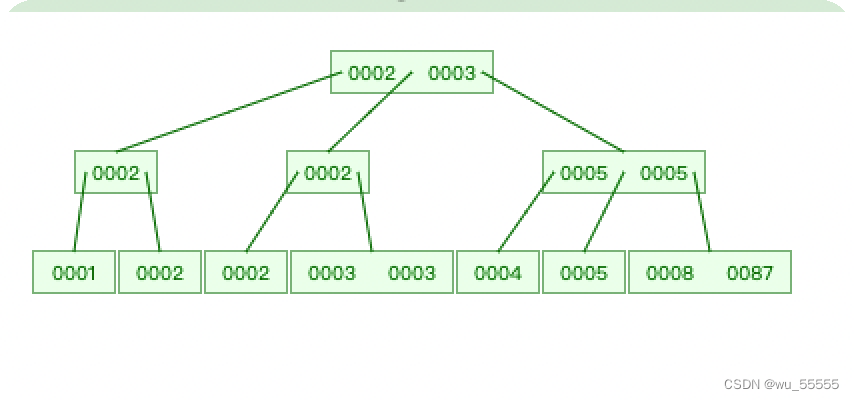我们经历了这么多的演变，终于实现了容量的提升，可是你觉得万事大吉了吗？
我们来深入的讲解一下树中每个节点的结构，如图所示，树中的每个节点我们称之为数据页，大小为16KB。也就是说每个节点只能装16KB的数据，装满就挪到下一个节点中。
而B树中每个节点中，不仅要装索引值，而且要装该索引对应的数据。是一个key-value结构，如果是主键索引，那么key就是主键值，那么value就是行数据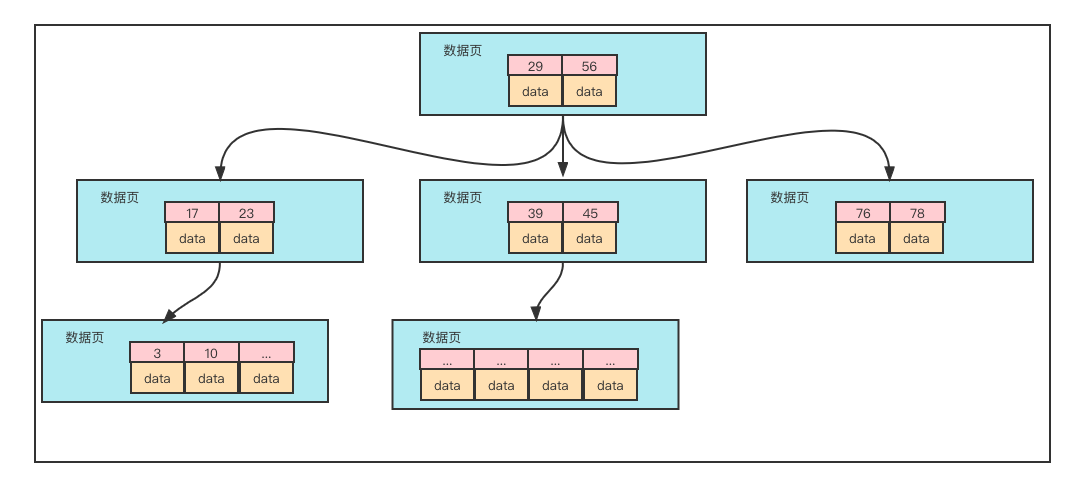 
这样的结构意味着什么呢？随着数据量的持续增加，因为数据页大小固定为16KB，又因为节点既要装索引值，又要装索引对应的数据，索引值一般很小，数据会占用大部分的空间，使得每个节点能装的索引其实不多，那么树的高度又会不断的变高。
树越高，IO越多，查询越慢。于是乎～性能瓶颈又来了。
怎么办呢？
既然因为data占用了极大部分的空间，那么我们能不能不在节点能放data数据呢？答案是不行，因为我们的目的是要根据索引找到数据，根本目的是数据，而不是索引，所以去掉数据肯定不行。
但是我们可以给数据换个位置
3.5 B+树B+树的处理更加聪明了，我们只在叶子节点中存储数据，非叶子节点中只存储索引以及指向下个节点的指针。
这样的处理方案，是的非叶子节点能够存储的索引数据会大大增加，那么树整体的高度就会下降。从而提高查询效率
同时B+树还在叶子节点之间加上了双向指针，使得分页查找的速度也大大提升。当需要进行遍历操作的时候直接通过叶子节点的链表查询 
同时大家还需要注意的是，非主键索引中，data存储的是主键数据，而在主键索引中，不同的存储引擎会存储不同的数据：
- innodb：主键索引的叶子节点，存储的是行数据，也体现出innodb存储方式采用的是聚簇索引，即innodb的索引和数据是放在同一个文件里存储的
- myisam: 主键索引的叶子节点，存储的是指向行数据的内存地址，并没有真正存储行数据，体现出采用的是非聚簇索引，所以miysam的数据和索引是放在两个文件里分开存储的。
到了这里，大家明白我们在一开始提出的几个问题应该怎么回答了吗？一定要自己理解，并且总结，然后再复述出来，学会将知识点输出出来。
本期的分享就到此结束了，如果你想要进阶学习mysql的调优知识，不妨关注专栏，我们下期见～
