0.1 算法分类
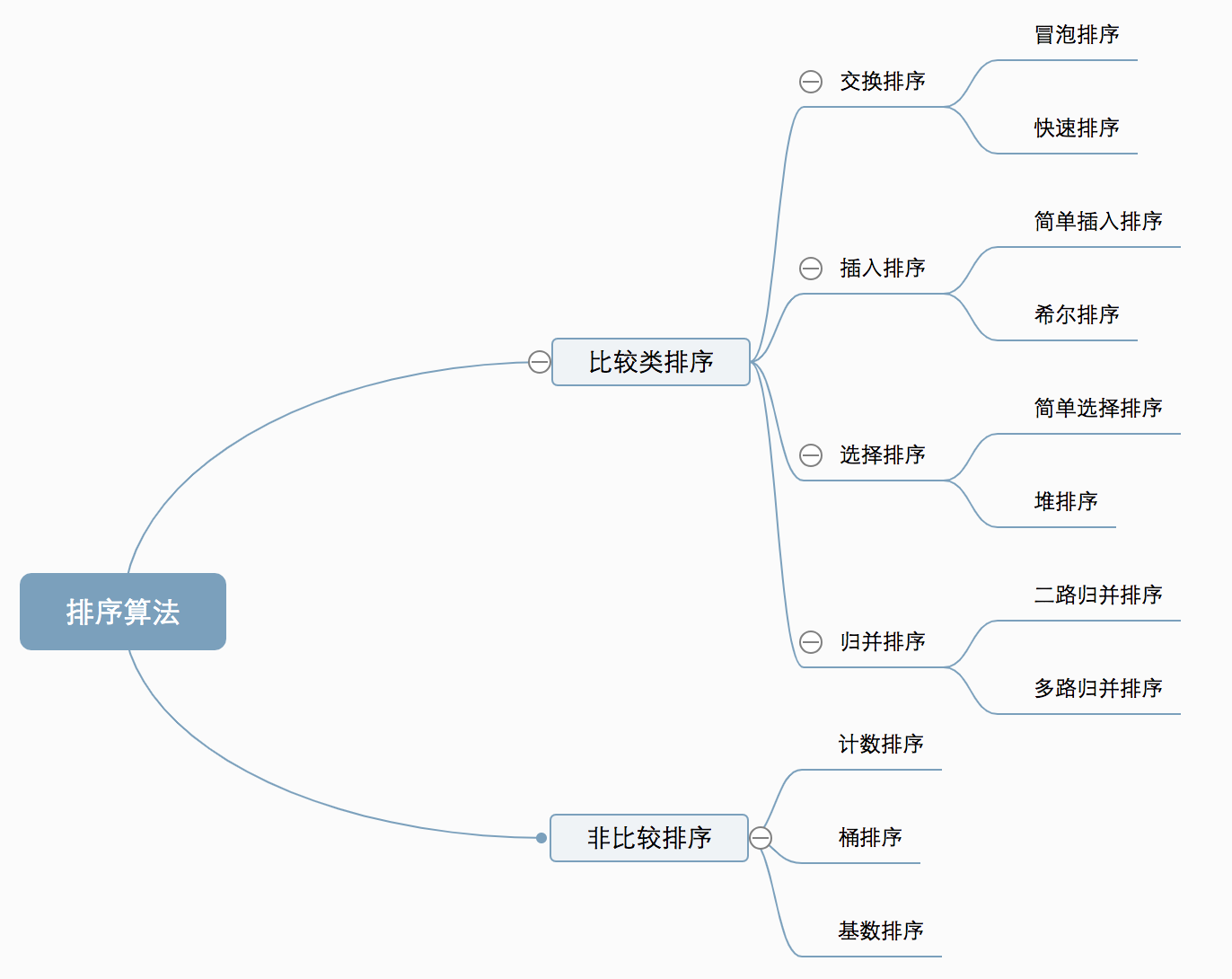
十种常见排序算法可以分为两大类:
- 比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。
- 非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。
0.2 算法复杂度
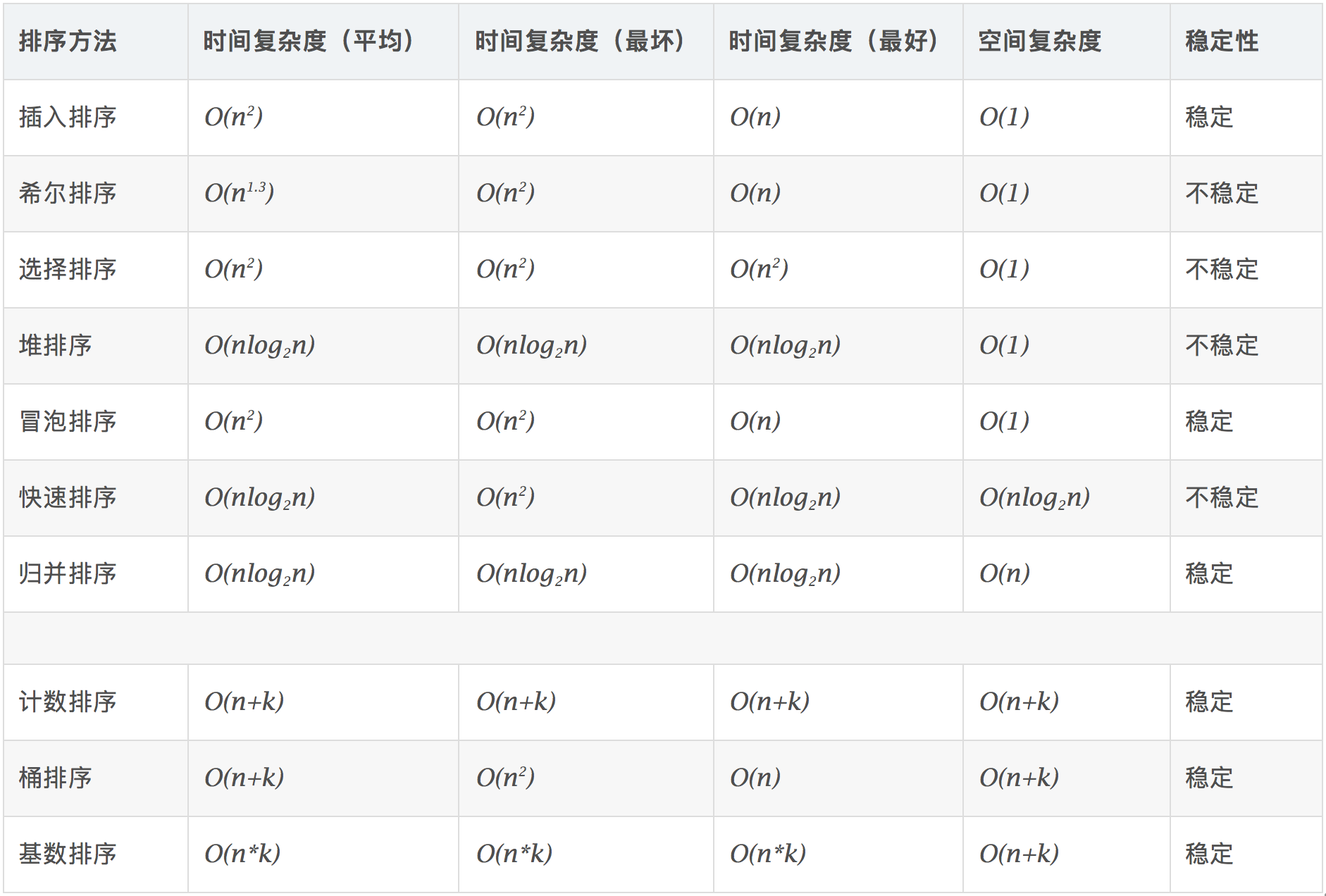
0.3 相关概念
- 稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
- 不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
- 时间复杂度:对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
- 空间复杂度:是指算法在计算机
内执行时所需存储空间的度量,它也是数据规模n的函数。
1、冒泡排序(Bubble Sort)冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
1.1 算法描述
- 比较相邻的元素。如果第一个比第二个大,就交换它们两个;
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
- 针对所有的元素重复以上的步骤,除了最后一个;
- 重复步骤1~3,直到排序完成。
1.2 动图演示
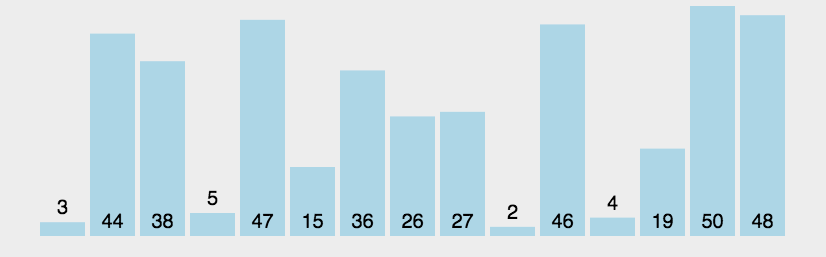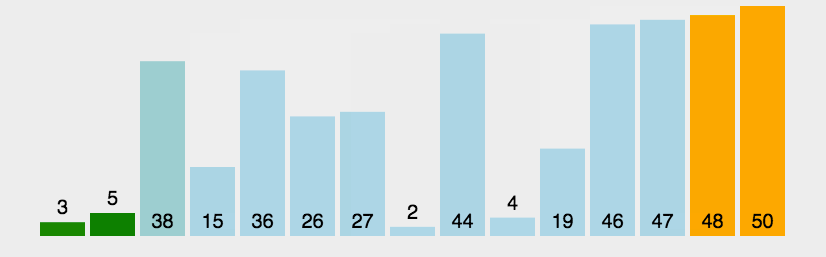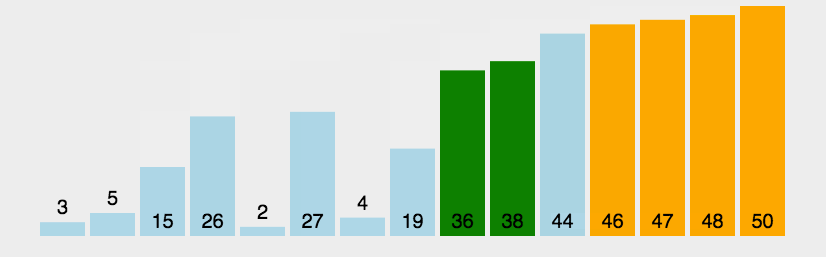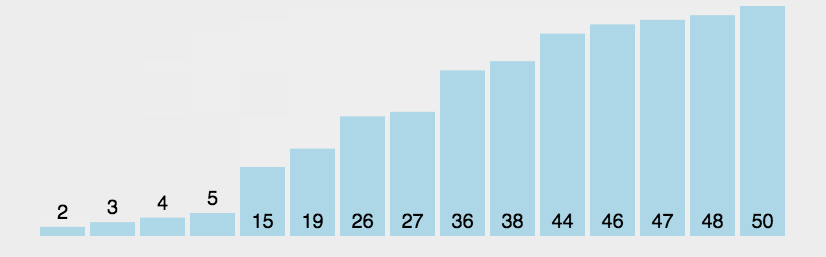

1.3 代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
function bubbleSort(arr) {
var len = arr.length;
for (var i = 0; i < len - 1; i++) {
for (var j = 0; j < len - 1 - i; j++) {
if (arr[j] > arr[j+1]) { // 相邻元素两两对比
var temp = arr[j+1]; // 元素交换
arr[j+1] = arr[j];
arr[j] = temp;
}
}
}
return arr;
}
import java.util.Arrays; public class BubbleSort { public static void main(String[] args) { int[] arr = {1,4,3,7,5}; bubbleSort(arr); } public static void bubbleSort(int[] arr){ for(int i=0;i 0; gap = Math.floor(gap / 2)) {
// 注意:这里和动图演示的不一样,动图是分组执行,实际操作是多个分组交替执行
for(vari = gap; i < len; i++) {
varj = i;
varcurrent = arr[i];
while(j - gap >= 0 && current < arr[j - gap]) {
arr[j] = arr[j - gap];
j = j - gap;
}
arr[j] = current;
}
}
returnarr;
}4.4 算法分析
希尔排序的核心在于间隔序列的设定。既可以提前设定好间隔序列,也可以动态的定义间隔序列。动态定义间隔序列的算法是《算法(第4版)》的合著者Robert Sedgewick提出的。
5、归并排序(Merge Sort)归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
5.1 算法描述
- 把长度为n的输入序列分成两个长度为n/2的子序列;
- 对这两个子序列分别采用归并排序;
- 将两个排序好的子序列合并成一个最终的排序序列。
5.2 动图演示
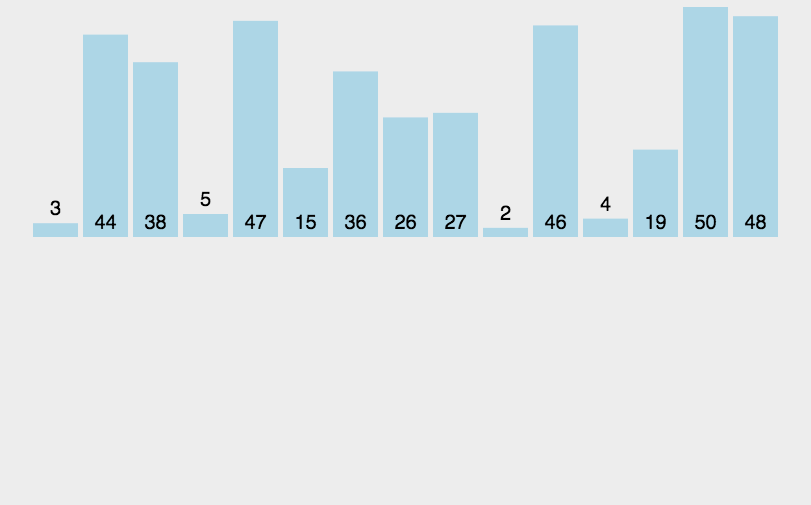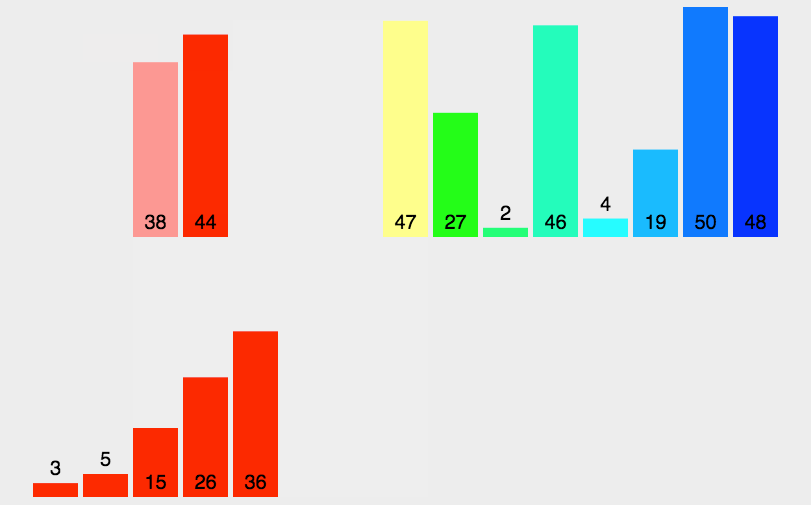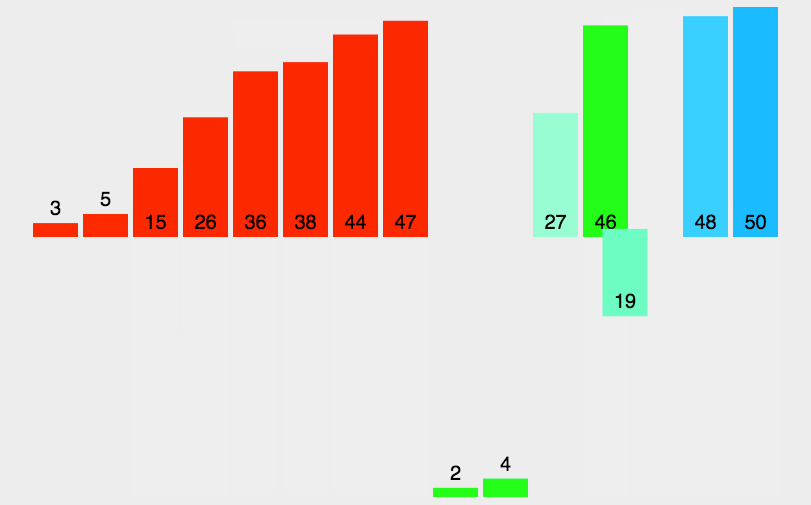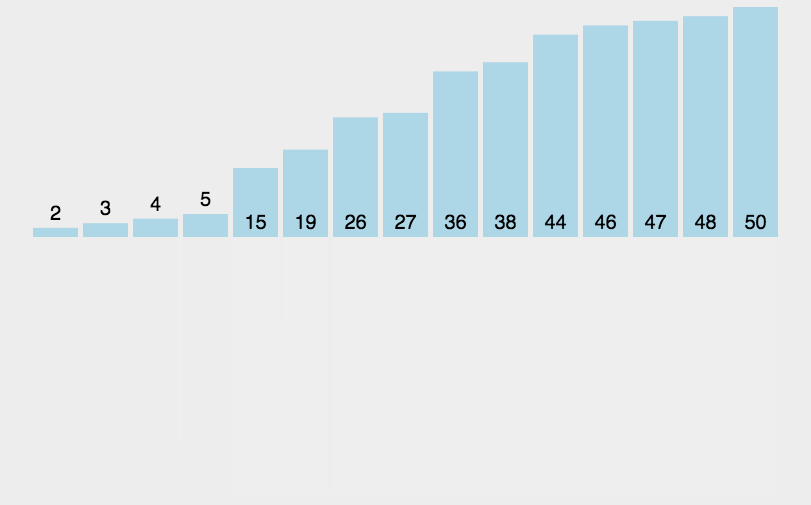
5.3 代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
function mergeSort(arr) {
var len = arr.length;
if (len < 2) {
return arr;
}
var middle = Math.floor(len / 2),
left = arr.slice(0, middle),
right = arr.slice(middle);
return merge(mergeSort(left), mergeSort(right));
}
function merge(left, right) {
var result = [];
while (left.length>0 && right.length>0) {
if (left[0] = high) {
return;
}
int i = low, j = high, index = arr[i];
while (i < j) {
while (i < j && arr[j] >= index) {
j--;
}
if (i < j) {
arr[i++] = arr[j];
}
while (i < j && arr[i] < index) {
i++;
}
if (i < j) {
arr[j--] = arr[i];
}
}
arr[i] = index;
quickSort(arr, low, i - 1);
quickSort(arr, i + 1, high);
}
public static void quick(int[] arr) {
quickSort(arr, 0, arr.length - 1);
}
public static void main(String[] args) {
int[] arr = new int[]{4, 5, 2, 7, 3, 8, 2};
quick(arr);
System.out.println(Arrays.toString(arr));
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
function quickSort(arr, left, right) {
var len = arr.length,
partitionIndex,
left =typeof left !='number' ? 0 : left,
right =typeof right !='number' ? len - 1 : right;
if (left < right) {
partitionIndex = partition(arr, left, right);
quickSort(arr, left, partitionIndex-1);
quickSort(arr, partitionIndex+1, right);
}
return arr;
}
function partition(arr, left ,right) { // 分区操作
var pivot = left, // 设定基准值(pivot)
index = pivot + 1;
for (var i = index; i arr[largest]) {
largest = left;
}
if (right < len && arr[right] > arr[largest]) {
largest = right;
}
if (largest != i) {
swap(arr, i, largest);
heapify(arr, largest);
}
}
function swap(arr, i, j) {
var temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
function heapSort(arr) {
buildMaxHeap(arr);
for (var i = arr.length - 1; i > 0; i--) {
swap(arr, 0, i);
len--;
heapify(arr, 0);
}
return arr;
}
计数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
8.1 算法描述
- 找出待排序的数组中最大和最小的元素;
- 统计数组中每个值为i的元素出现的次数,存入数组C的第i项;
- 对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加);
- 反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1。
8.2 动图演示
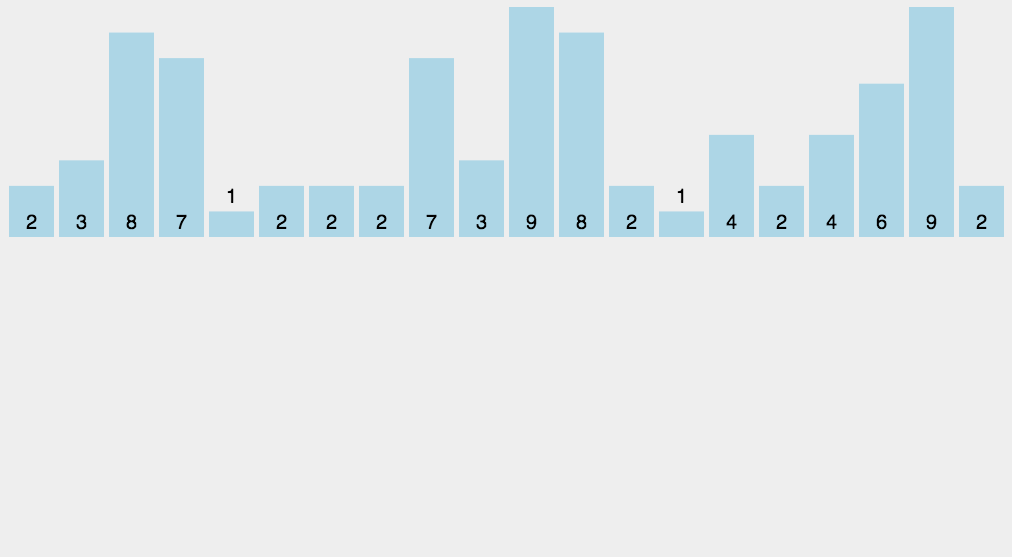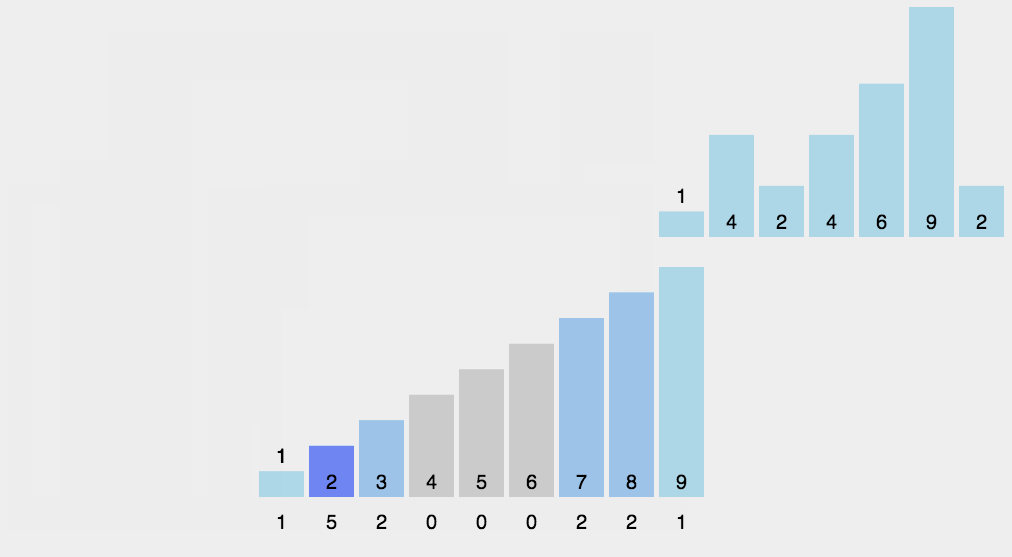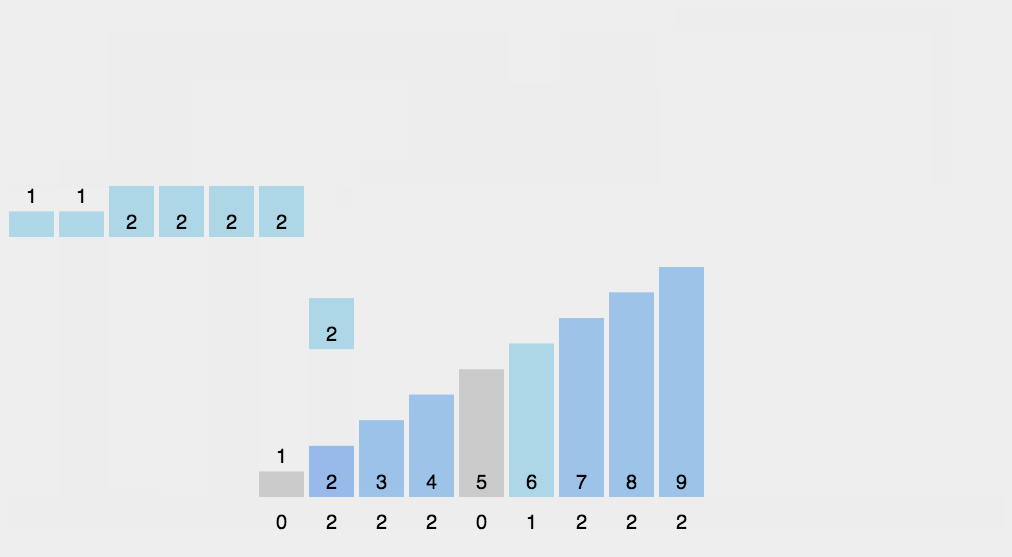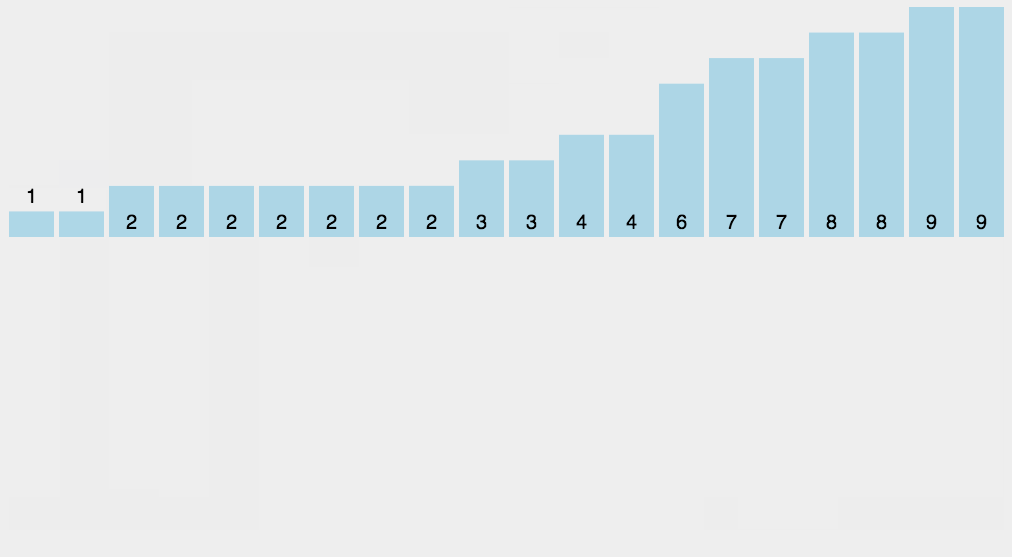
8.3 代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
function countingSort(arr, maxValue) {
var bucket =new Array(maxValue + 1),
sortedIndex = 0;
arrLen = arr.length,
bucketLen = maxValue + 1;
for (var i = 0; i < arrLen; i++) {
if (!bucket[arr[i]]) {
bucket[arr[i]] = 0;
}
bucket[arr[i]]++;
}
for (var j = 0; j < bucketLen; j++) {
while(bucket[j] > 0) {
arr[sortedIndex++] = j;
bucket[j]--;
}
}
return arr;
}
8.4 算法分析
计数排序是一个稳定的排序算法。当输入的元素是 n 个 0到 k 之间的整数时,时间复杂度是O(n+k),空间复杂度也是O(n+k),其排序速度快于任何比较排序算法。当k不是很大并且序列比较集中时,计数排序是一个很有效的排序算法。
9、桶排序(Bucket Sort)桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。桶排序 (Bucket sort)的工作的原理:假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排)。
9.1 算法描述
- 设置一个定量的数组当作空桶;
- 遍历输入数据,并且把数据一个一个放到对应的桶里去;
- 对每个不是空的桶进行排序;
- 从不是空的桶里把排好序的数据拼接起来。
9.2 图片演示
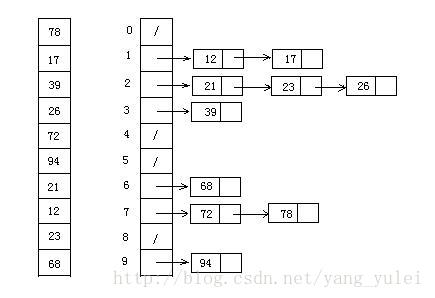
9.3 代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
function bucketSort(arr, bucketSize) {
if (arr.length === 0) {
return arr;
}
var i;
var minValue = arr[0];
var maxValue = arr[0];
for (i = 1; i < arr.length; i++) {
if (arr[i] < minValue) {
minValue = arr[i]; // 输入数据的最小值
}else if (arr[i] > maxValue) {
maxValue = arr[i]; // 输入数据的最大值
}
}
// 桶的初始化
var DEFAULT_BUCKET_SIZE = 5; // 设置桶的默认数量为5
bucketSize = bucketSize || DEFAULT_BUCKET_SIZE;
var bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;
var buckets =new Array(bucketCount);
for (i = 0; i < buckets.length; i++) {
buckets[i] = [];
}
// 利用映射函数将数据分配到各个桶中
for (i = 0; i < arr.length; i++) {
buckets[Math.floor((arr[i] - minValue) / bucketSize)].push(arr[i]);
}
arr.length = 0;
for (i = 0; i < buckets.length; i++) {
insertionSort(buckets[i]); // 对每个桶进行排序,这里使用了插入排序
for (var j = 0; j < buckets[i].length; j++) {
arr.push(buckets[i][j]);
}
}
return arr;
}
9.4 算法分析
桶排序最好情况下使用线性时间O(n),桶排序的时间复杂度,取决与对各个桶之间数据进行排序的时间复杂度,因为其它部分的时间复杂度都为O(n)。很显然,桶划分的越小,各个桶之间的数据越少,排序所用的时间也会越少。但相应的空间消耗就会增大。
10、基数排序(Radix Sort)基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。
10.1 算法描述
- 取得数组中的最大数,并取得位数;
- arr为原始数组,从最低位开始取每个位组成radix数组;
- 对radix进行计数排序(利用计数排序适用于小范围数的特点);
10.2 动图演示

10.3 代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
var counter = [];
function radixSort(arr, maxDigit) {
var mod = 10;
var dev = 1;
for (var i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
for(var j = 0; j < arr.length; j++) {
var bucket = parseInt((arr[j] % mod) / dev);
if(counter[bucket]==null) {
counter[bucket] = [];
}
counter[bucket].push(arr[j]);
}
var pos = 0;
for(var j = 0; j < counter.length; j++) {
var value =null;
if(counter[j]!=null) {
while ((value = counter[j].shift()) !=null) {
arr[pos++] = value;
}
}
}
}
return arr;
}
10.4 算法分析
基数排序基于分别排序,分别收集,所以是稳定的。但基数排序的性能比桶排序要略差,每一次关键字的桶分配都需要O(n)的时间复杂度,而且分配之后得到新的关键字序列又需要O(n)的时间复杂度。假如待排数据可以分为d个关键字,则基数排序的时间复杂度将是O(d*2n) ,当然d要远远小于n,因此基本上还是线性级别的。
基数排序的空间复杂度为O(n+k),其中k为桶的数量。一般来说n>>k,因此额外空间需要大概n个左右。
十大经典排序算法(动图演示) - 一像素 - 博客园



