平衡二叉树与java实现

平衡二叉树

定义

亦称为AVL

空树和1个点节点的树都是平衡二叉树

平衡二叉树是在二叉排序树上的扩展延伸，除了自身的性质还满足以下性质的二叉树：

• 树中的子树都是平衡二叉树
• 每颗子树的左子树和右子树的深度之差的绝对值不超过1。

结点的平衡因子BF（balance factor）

该结点的左子树的深度减去右子树的深度，则平衡二叉树上所有节点的平衡因子的值为-1，0，1。

查询，删除过程

它的查询和删除系列操作思路跟二叉排序树差不多，可以阅读二叉排序树的JAVA实现

检查平衡

通过计算每个结点的平衡因子来判断是否平衡。只要平衡因子为2 或 -2，就说明此结点子树不平衡。

平衡操作–左旋和右旋

当平衡二叉树由于新增数据元素导致整棵树的平衡遭到破坏时，就需要根据实际情况做出适当的调整，寻找距离插入结点最近的“不平衡因子”。则调整的规律可归纳为以下 4 种情况：

• 单向右旋平衡处理：若由于结点A的左子树为根结点的左子树上插入结点，导致结点A的平衡因子由 1 增至 2，致使以A为根结点的子树失去平衡，则只需进行一次向右的顺时针旋转，如下图这种情况：

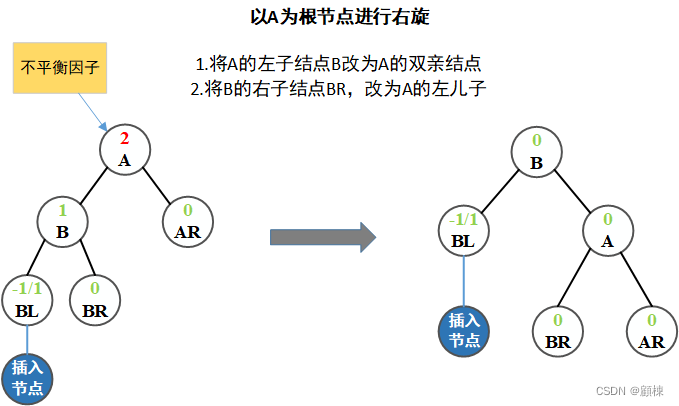
• 单向左旋平衡处理：如果由于结点A的右子树为根结点的右子树上插入结点，导致结点A的平衡因子由 -1变为 -2，则以A为根结点的子树需要进行一次向左的逆时针旋转，如下图这种情况：

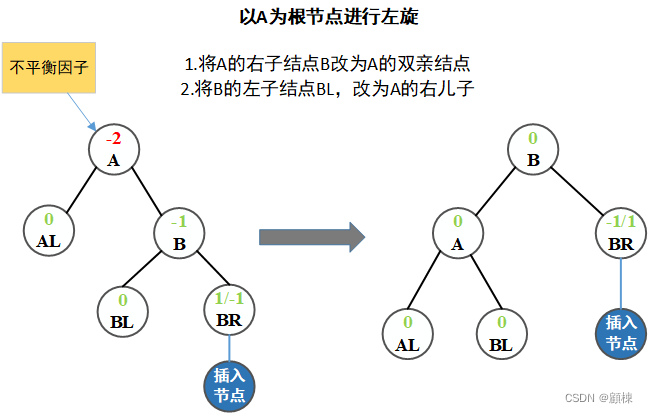
• 双向旋转（先左后右）平衡处理：如果由于结点A的左子树为根结点的右子树上插入结点，导致结点A衡因子由 1 增至 2，致使以A为根结点的子树失去平衡，则需要进行两次旋转操作，先以A的左子结点B为根结点进行左旋，在以A为根结点进行右旋，如下图这种情况：

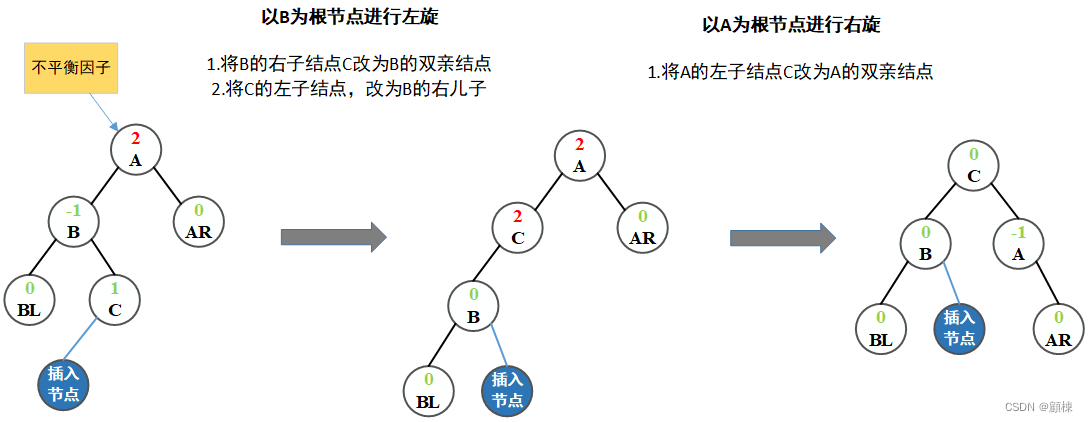
• 双向旋转（先右后左）平衡处理：如果由于结点 A 的右子树为根结点的左子树上插入结点，导致结点 A 平衡因子由 -1 变为 -2，致使以 a 为根结点的子树失去平衡，则需要进行两次旋转操作，先以A的左子结点B为根结点进行右旋，在以A为根结点进行左旋，如下图这种情况：

JAVA代码实现

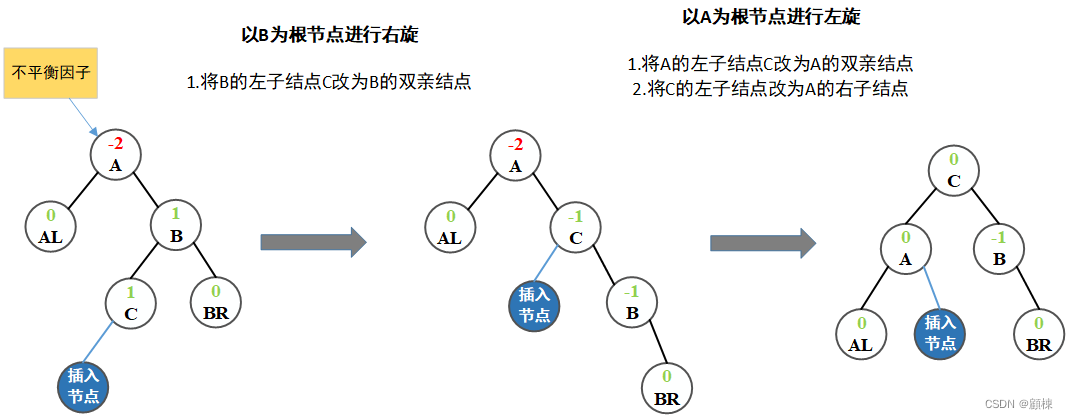
package tree.avl;

import org.apache.commons.lang.StringUtils;

import java.util.LinkedList;
import java.util.Queue;

/**
 * @author Donny
 * @date 2022/5/18
 */
public class AvlTree {

    public static final StringBuilder VALUES = new StringBuilder();
    public static final String SEPARATOR = "->";
    public static final int SEPARATOR_LENGTH = SEPARATOR.length();

    /**
     * 右子树需要平衡操作
     */
    private final int RIGHT = 0;
    
    /**
     * 左子树需要平衡操作
     */
    private final int LEFT = 1;
    
    /**
     * 树根
     */
    private AvlTreeNode root;

    /**
     * 树的结点类
     */
    private static class AvlTreeNode {
        /**
         * 存储的数值
         */
        private int data;
        /**
         * 左子结点
         */
        private AvlTreeNode leftChild;
        /**
         * 右子结点
         */
        private AvlTreeNode rightChild;
        /**
         * 双亲结点
         */
        private AvlTreeNode parentNode;

        public AvlTreeNode(int data) {
            this(data, null, null, null);
        }

        public AvlTreeNode(int data, AvlTreeNode parentAvlTreeNode) {
            this(data, null, null, parentAvlTreeNode);
        }

        public AvlTreeNode(int data, AvlTreeNode leftAvlTreeNode, AvlTreeNode rightAvlTreeNode, AvlTreeNode parentAvlTreeNode) {
            this.data = data;
            this.leftChild = leftAvlTreeNode;
            this.rightChild = rightAvlTreeNode;
            this.parentNode = parentAvlTreeNode;
        }

        /**
         * 计算结点的高度
         */
        public int height() {
            return Math.max(leftChild == null ? 0 : leftChild.height(), rightChild == null ? 0 : rightChild.height()) + 1;
        }

        /**
         * 左子树的高度
         */
        public int leftHeight() {
            if (leftChild == null) {
                return 0;
            } else {
                return leftChild.height();
            }
        }

        /**
         * 右子树的高度
         */
        public int rightHeight() {
            if (rightChild == null) {
                return 0;
            } else {
                return rightChild.height();
            }
        }

        /**
         * 计算平衡因子
         */
        public int calcBalanceFactor() {
            return leftHeight() - rightHeight();
        }
    }

    /**
     * 以node为根结点 左旋
     */
    public AvlTreeNode leftRotation(AvlTreeNode node) {

        if (node != null) {
            // 将当前结点的双亲结点转移给当前结点的右子结点
            AvlTreeNode rightChild = node.rightChild;
            // 右子结点的左子结点作为当前结点的右结点
            node.rightChild = rightChild.leftChild;
            if (rightChild.leftChild != null) {
                rightChild.leftChild.parentNode = node;
            }
            // 右子结点的双亲结点变为当前结点的双亲结点
            rightChild.parentNode = node.parentNode;
            // 判断当前结点的父结点是否存在
            if (node.parentNode == null) {
                this.root = rightChild;
            }
            /*
             * 当前结点结点不是根结点 分两种情况
             *   1、当前结点结点位于其父结点左边，则原左子结点也要位于左边
             *   2、当前结点结点位于其父结点右边，则原左子结点也要位于右边
             */
            else if (node.parentNode.rightChild == node) {
                node.parentNode.rightChild = rightChild;
            } else if (node.parentNode.leftChild == node) {
                node.parentNode.leftChild = rightChild;
            }
            // 将右子结点的左子结点改为当前结点
            rightChild.leftChild = node;
            // 将原右子结点当前结点的双亲结点
            node.parentNode = rightChild;

        }
        return null;
    }

    /**
     * 以node为根结点 右旋
     */
    public AvlTreeNode rightRotation(AvlTreeNode node) {
        if (node != null) {
            // 用变量存储node结点的左子结点
            AvlTreeNode leftChild = node.leftChild;
            // 将leftChild结点的右子结点赋值给node结点的左结点
            node.leftChild = leftChild.rightChild;
            // 如果leftChild的右结点存在，则需将该右结点的父结点指给node结点
            if (leftChild.rightChild != null) {
                leftChild.rightChild.parentNode = node;
            }

            // 将当前结点的双亲结点转移给当前结点的左子结点
            leftChild.parentNode = node.parentNode;
            if (node.parentNode == null) {
                // 即表明node结点为根结点
                this.root = leftChild;
            }
            /*
             * 当前结点结点不是根结点 分两种情况
             *   1、当前结点结点位于其父结点左边，则原左子结点也要位于左边
             *   2、当前结点结点位于其父结点右边，则原左子结点也要位于右边
             */
            else if (node.parentNode.rightChild == node) {
                // 即node结点在它原父结点的右子树中
                node.parentNode.rightChild = leftChild;
            } else if (node.parentNode.leftChild == node) {
                node.parentNode.leftChild = leftChild;
            }
            leftChild.rightChild = node;
            node.parentNode = leftChild;
            return leftChild;
        }
        return null;
    }

    /**
     * 新增key
     */
    public void insert(int key) {
        // 若树根为null 则新建结点作为树根
        if (null == root) {
            root = new AvlTreeNode(key);
            return;
        }

        // p作为遍历树结点的临时帮助结点
        AvlTreeNode p = root;
        // prev代表新增key的结点的双亲结点
        AvlTreeNode prev = null;
        while (null != p) {
            prev = p;
            if (key > p.data) {
                p = p.rightChild;
            } else if (key  prev.data) {
            // 新增结点是prev的右子结点
            prev.rightChild = node;
        } else {
            // 新增结点是prev的左子结点
            prev.leftChild = node;
        }

        rebuild(prev);
    }

    /**
     * 计算结点的平衡因子进行平衡操作
     * 平衡因子为-1,0,1是为平衡的，所有一旦平衡因子为2或-2就需要进行平衡操作。
     */
    private void rebuild(AvlTreeNode p) {
        while (p != null) {
            if (p.calcBalanceFactor() == 2) {
                // 说明左子树高，需要【右旋】或者【先左旋后右旋】
                fixAfterInsertion(p, LEFT);
            } else if (p.calcBalanceFactor() == -2) {
                // 说明右子树高，需要【左旋】或者【先右旋后左旋】
                fixAfterInsertion(p, RIGHT);
            }
            p = p.parentNode;
        }
    }

    private void fixAfterInsertion(AvlTreeNode p, int type) {
        // 左子树失衡
        if (type == LEFT) {
            final AvlTreeNode leftChild = p.leftChild;
            // 左子结点不为空，直接右旋
            if (leftChild.leftChild != null) {
                //LL型
                rightRotation(p);
            } else if (leftChild.rightChild != null) {
                // 先左旋后右旋 LR型
                leftRotation(leftChild);
                rightRotation(p);
            }
        } else {
            // 右子树失衡
            final AvlTreeNode rightChild = p.rightChild;
            // 右子结点不为空，直接左旋
            if (rightChild.rightChild != null) {
                // 左旋 RR型
                leftRotation(p);
            } else if (rightChild.leftChild != null) {
                // 先右旋，后左旋 RL型
                rightRotation(p);
                leftRotation(rightChild);
            }
        }
    }

    /**
     * 中序输出
     */
    public String inOrderPrint() {
        return inOrderPrint(this.root);
    }

    /**
     * 中序输出
     */
    private String inOrderPrint(AvlTreeNode node) {
        String result = "";
        if (node != null) {
            inOrderPrint(node.leftChild);
            VALUES.append(node.data).append(SEPARATOR);
            inOrderPrint(node.rightChild);
        }
        if (StringUtils.isNotBlank(VALUES.toString())) {
            result = VALUES.substring(0, VALUES.toString().length() - SEPARATOR_LENGTH);
        }
        return result;
    }

    public void printLeft() {
        if (this.root == null) {
            return;
        }
        Queue queue = new LinkedList();
        AvlTreeNode temp;
        queue.add(root);
        while (!queue.isEmpty()) {
            temp = queue.poll();
            System.out.print("结点值：" + temp.data + ",平衡值:" + temp.calcBalanceFactor() + "\n");
            if (temp.leftChild != null) {
                queue.add(temp.leftChild);
            }
            if (temp.rightChild != null) {
                queue.add(temp.rightChild);
            }
        }
    }

    public AvlTreeNode getNode(int value) {
        AvlTreeNode temp = root;
        int t;
        do {
            t = temp.data - value;
            if (t > 0) {
                temp = temp.leftChild;
            } else if (t