红黑树图解与JAVA实现

红黑树与JAVA实现

定义

红黑树是一种平衡二叉查找树。红黑树的每个结点上会多出一个存储位表示结点的颜色，颜色只能是红色或黑色。

特性

1. 每个结点的或是黑色或是红色 2. 根结点是黑色 3. 每个叶子结点都是黑色（NIL） 4. 如果一个结点是红色，那么他的子结点必须是黑色 5. 对任意一结点，该结点到其叶结点树尾端NIL指针的每一条路径都包含相同数目的黑结点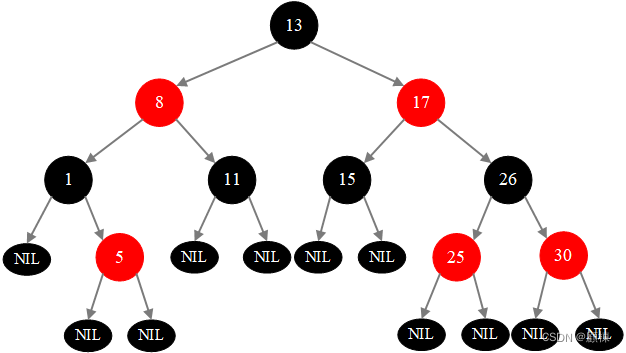

平衡操作

变色+左旋/右旋

左旋

对A结点进行左旋 就是将A结点的右子结点设为A的父结点，即将A结点变为一个左结点。

右旋

对A结点进行右旋 就是将A结点的左子结点设为A的父结点，即将A结点变为一个右结点。

主要过程 插入过程

向上回溯满足特性

新插入的结点总是设为红色的，所以如果父结点为黑色，就不需要修复，因为没有任何性质被改变，所以只有在父结点为红色结点时需要做修复操作。

父结点是祖父结点的左子结点 情况1：当前结点P的父结点B是红色，且祖父结点的另一个子结点（叔叔结点）C也是红色

对策 :

• 变色：把父结点B和叔叔结点B变黑，祖父A结点涂红
• 向上回溯：然后把当前结点指针给到爷爷，让祖父结点那层继续循环，接受红黑树特性检测。直到根结点，将根结点保持为黑色。

情况2：当前结点P的父结点B是红色，叔叔结点C是黑色，且当前结点是其父结点的左子结点

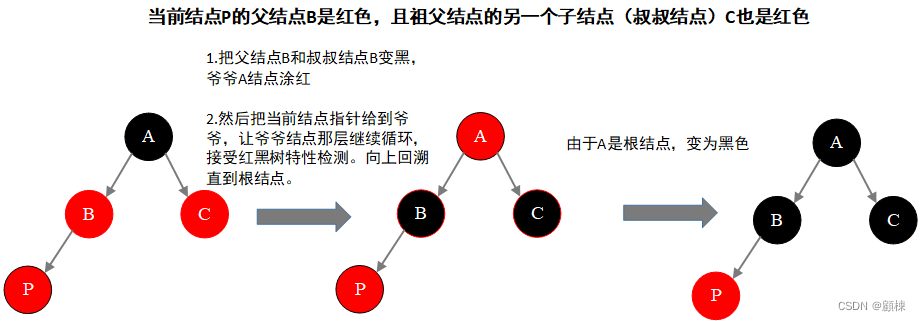
对策：

• 变色：把父结点B变黑，祖父结点A变红
• 旋转：以祖父结点A为支点右旋

情况3：当前结点P的父结点B是红色，叔叔结点C是黑色，当前结点是父结点的右子结点

对策：

• 旋转：以P的父结点B作为支点左旋
• 当前结点改为P的父结点B
• 此时情况与情况2一致，执行情况2的对策操作。

父结点是祖父结点的右子结点 情况1：父结点与叔叔结点都是红色

对策 :

• 变色：把父结点B和叔叔结点B变黑，祖父A结点涂红
• 向上回溯：然后把当前结点指针给到祖父，让祖父结点那层继续循环，接受红黑树特性检测。直到根结点，将根结点保持为黑色。

情况2：当前结点P的父结点B是红色，叔叔结点C是黑色，且当前结点是其父结点的右子结点

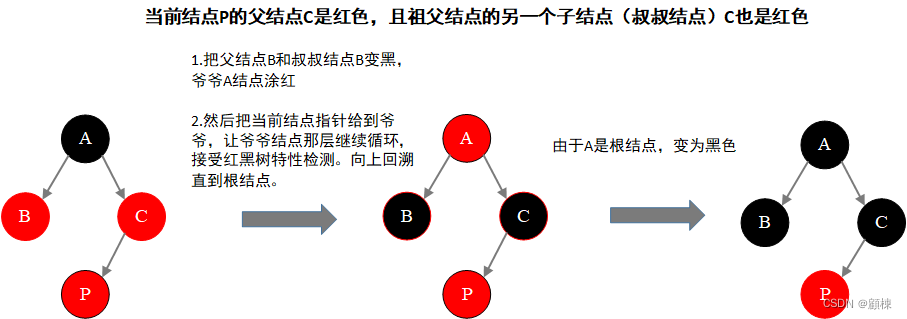
对策 :

• 变色：把父结点B变黑，祖父结点A变红
• 旋转：对祖父结点A进行左旋操作

情况3：当前结点P的父结点B是红色，叔叔结点C是黑色，且当前结点是其父结点的左子结点

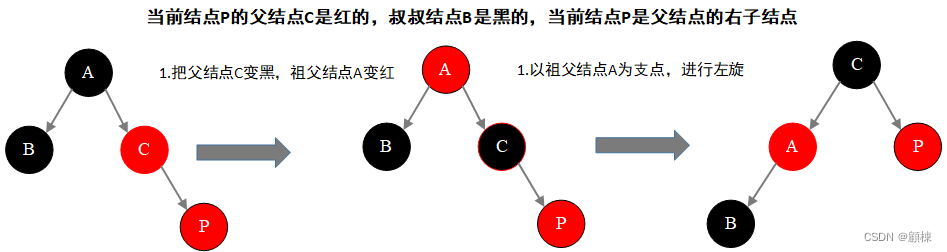
对策 :

• 把当前结点指向父结点C
• 旋转：以当前结点C进行右旋
• 此时情况与情况2一致，执行情况2的对策操作。

删除过程

在删除一个结点后，如果删除的结点时红色结点，那么红黑树的性质并不会被影响，此时不需要修正，如果删除的是黑色结点，原红黑树的性质就会被改变，此时我们需要做修正。

当前结点是父结点的左子结点 情况1：兄弟结点为红色

这个时候其实不用管左右侄子是什么颜色的。

对策 :

• 变色：将兄弟变成黑色，父结点变成红色
• 旋转：以父结点为根，进行左旋
• 此时结点情况可能会出现情况2,3,4中的一种

情况2：兄弟为黑色，左右侄子也是黑色

为了图解看上去是个红黑树，D的左右子结点采用了NIL表示。但是实际情况是除了是NIL情况下是黑色结点，会出现拥有实际值的黑色结点。例如全黑树。

对策 :

• 变色：兄弟变红
• 当前结点指向父结点，继续判断处理

情况3：兄弟为黑色，右侄子为黑色

为了图解看上去是个红黑树，B的右子结点采用了NIL表示。但是实际情况是除了是NIL情况下是黑色结点，会出现拥有实际值的黑色结点。

对策 :

• 变色：左侄子变为黑色，兄弟变红
• 旋转：以兄弟为支点右旋
• 此时应该是情况4的场景，继续处理

情况4：兄弟为黑色，右侄子为红色

对策 :

• 变色：兄弟颜色变为双亲结点的颜色，右侄子和双亲结点变为黑色。
• 旋转：以双亲结点为支点，左旋
• 跳出循环（将当前结点变为root）

当前结点是父结点的右子结点 情况1：兄弟结点为红色

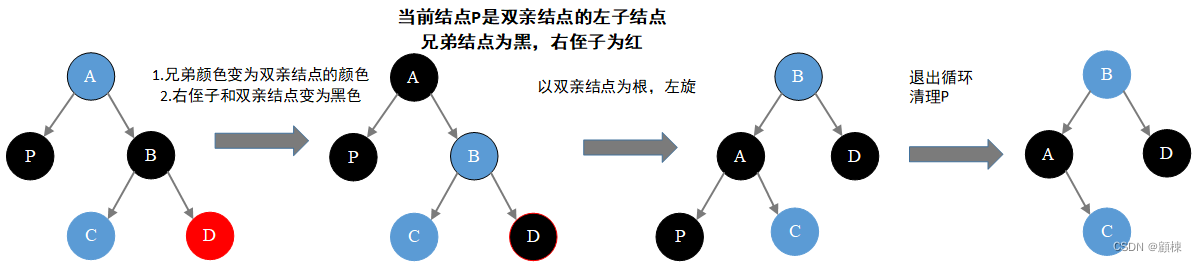
这个时候其实不用管左右侄子是什么颜色的。

对策 :

• 变色：将兄弟变成黑色，父结点变成红色
• 旋转：以父结点为支点，进行右旋
• 此时结点情况可能会出现情况2,3,4中的一种

情况2：兄弟结点为黑色，左右侄子也是黑色

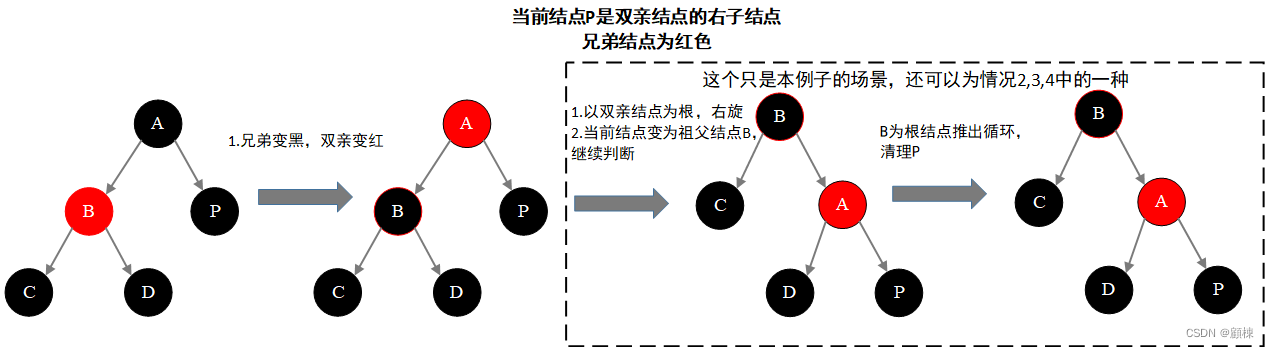
为了图解看上去是个红黑树，D的左右子结点采用了NIL表示。但是实际情况是除了是NIL情况下是黑色结点，会出现拥有实际值的黑色结点。例如全黑树。

对策 :

• 变色：兄弟变红，当前结点指向父结点
• 继续判断处理

情况3：兄弟结点为黑色，左侄子为黑色

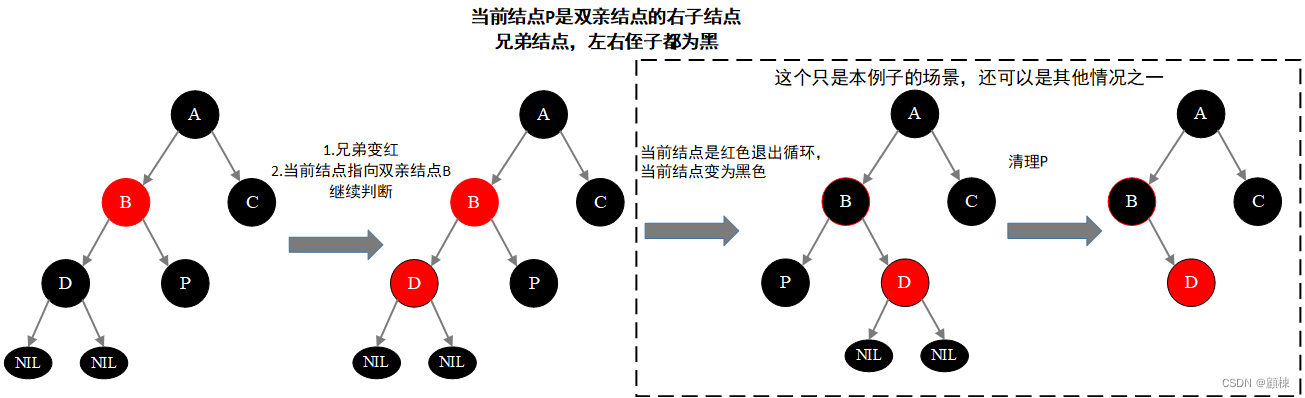
为了图解看上去是个红黑树，B的左子结点采用了NIL表示。但是实际情况是除了是NIL情况下是黑色结点，会出现拥有实际值的黑色结点。

对策 :

• 变色：右侄子变为黑色，兄弟变红
• 旋转：以兄弟为支点左旋
• 此时应该是情况4的场景，继续处理

情况4：兄弟结点为黑色，左侄子为红色

对策 :

• 变色：兄弟颜色变为双亲结点的颜色，左侄子和双亲结点变为黑色。
• 旋转：以双亲结点为支点，右旋
• 跳出循环（将当前结点变为root）

存储结构 三叉链表 colorvalueleftrightparent

    /**
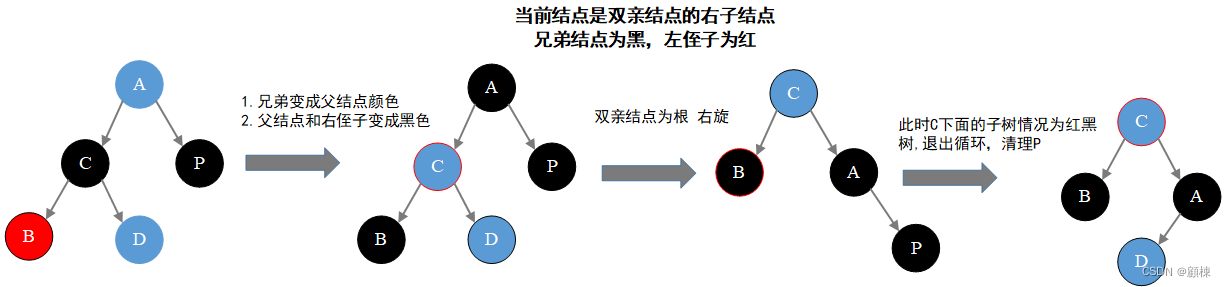
     * RB树的结点类
     */
    public static class RBNode {
        /**
         * 颜色
         */
        private boolean color;
        /**
         * 关键字(键值)
         */
        private T key;
        /**
         * 左孩子
         */
        private RBNode left;
        /**
         * 右孩子
         */
        private RBNode right;
        /**
         * 父结点
         */
        private RBNode parent;

        /**
         * 构造函数
         */
        public RBNode(T key, boolean color, RBNode parent, RBNode left, RBNode right) {
            this.key = key;
            this.color = color;
            this.parent = parent;
            this.left = left;
            this.right = right;
        }

        public RBNode(T key) {
            this(key, RED, null, null, null);
        }

        boolean isBlack() {
            return this.color;
        }

        boolean isRed() {
            return !this.color;
        }
    }

JAVA 实现

package tree.redblack;

import java.util.LinkedList;
import java.util.concurrent.atomic.AtomicLong;

/**
 * @author Donny
 * @date 2022/5/17 11:41
 */
public class RBTree {

    private static final boolean RED = false;
    private static final boolean BLACK = true;

    /**
     * 数中结点的数量
     */
    AtomicLong size = new AtomicLong(0);
    /**
     * 根结点
     */
    private RBNode root;

    public RBNode getRoot() {
        return root;
    }

    /**
     * RB树的结点类
     */
    public static class RBNode {
        /**
         * 颜色
         */
        private boolean color;
        /**
         * 关键字(键值)
         */
        private T key;
        /**
         * 左孩子
         */
        private RBNode left;
        /**
         * 右孩子
         */
        private RBNode right;
        /**
         * 父结点
         */
        private RBNode parent;

        /**
         * 构造函数
         */
        public RBNode(T key, boolean color, RBNode parent, RBNode left, RBNode right) {
            this.key = key;
            this.color = color;
            this.parent = parent;
            this.left = left;
            this.right = right;
        }

        public RBNode(T key, boolean color) {
            this(key, color, null, null, null);
        }

        public RBNode(T key) {
            this(key, RED, null, null, null);
        }

        public boolean isBlack() {
            return this.color;
        }

        public boolean isRed() {
            return !this.color;
        }
    }

    /**
     * 以node为支点左旋
     */
    private void leftRotate(RBNode node) {
        RBNode rightChild = node.right;
        if (null == rightChild) {
            throw new IllegalStateException("right is null");
        }
        RBNode parent = node.parent;
        node.right = rightChild.left;
        if (null != node.right) {
            node.right.parent = node;
        }

        rightChild.left = node;

        if (null == parent) {
            this.root = rightChild;
        } else if (node.parent.left == node) {
            parent.left = rightChild;
        } else {
            parent.right = rightChild;
        }
        node.parent = rightChild;
        rightChild.parent = parent;
    }

    /**
     * 以node为支点右旋
     */
    private void rightRotate(RBNode node) {
        RBNode leftChild = node.left;
        if (null == leftChild) {
            throw new IllegalStateException("leftChild is null");
        }

        RBNode parent = node.parent;
        node.left = leftChild.right;
        if (null != node.left) {
            node.left.parent = node;
        }
        leftChild.right = node;

        if (null == parent) {
            this.root = leftChild;
        } else if (node.parent.left == node) {
            parent.left = leftChild;
        } else {
            parent.right = leftChild;
        }
        node.parent = leftChild;
        leftChild.parent = parent;
    }

    public T insert(T key) {
        RBNode rbNode = new RBNode(key);
        return insert(rbNode);
    }

    public T insert(RBNode node) {
        int cmp;
        RBNode y = null;
        RBNode x = this.root;

        // 将红黑树当作一颗二叉查找树，将结点添加到二叉查找树中
        while (x != null) {
            y = x;
            cmp = node.key.compareTo(x.key);
            if (cmp == 0) {
                T v = x.key;
                x.key = node.key;
                return v;
            } else if (cmp