【高级UI】【019】通过Matrix变换Canvas坐标系

前言

关于矩阵运算规则，我们在前面已经讲过

Matrix在绘图方面，很多地方都能用到，不同的矩阵，格式不一样，功能也不一样

像我们前面提到的ColorMatrix，可以用来进行色彩变换

此外，Matrix还可以应用于画笔，画布，它能将本来应该绘制在（x，y）位置的坐标，自动转为（x’，y’）

试想，如果没有Matrix帮我们自动转换，我们做个旋转，拉伸，平移，都要自己去处理，那真是太恐怖了

Matrix本身不难，前面我们也已经用到过不少次

这篇博客，主要是为了给大家讲解下，Matrix底层的具体实现规则和工作原理

这样等大家以后技术上去了，自己也可以利用矩阵去解决一些图形变换类的工作

Canvas中的Matrix格式

Canvas中的Matrix是一个3*3的矩阵，格式如下

[ s c a l e X s k e w X t r a n X s k e w Y s c a l e Y t r a n Y p e r s p 1 p e r s p 2 p e r s p 3 ] \begin{bmatrix} &scaleX &skewX &tranX&\\ &skewY &scaleY &tranY&\\ &persp1 &persp2 &persp3&\\ \end{bmatrix} ⎣⎡​​scaleXskewYpersp1​skewXscaleYpersp2​tranXtranYpersp3​​⎦⎤​

scale用于缩放，skew用于错切，tran用于平移

并没有提供rotate参数来进行旋转，因为通过scale和skew的组合，也可以实现rotate的功能

persp参数是用于3D透视的，二维绘图不用考虑，persp3永远为1，其它两个永远为0

Matrix坐标转换公式

以下是Matrix坐标转换公式

知道公式后，我们给矩阵中的变量，设置合适的值，就能达到缩放，错切，平移，旋转等功能了

这个并不难，几何好的同学，自己想象下也能推导出来

当然，我会照顾到所有人，下面会给出每种效果的具体矩阵值

[ x ′ y ′ 1 ] = [ s c a l e X s k e w X t r a n X s k e w Y s c a l e Y t r a n Y p e r s p 1 p e r s p 2 p e r s p 3 ] ∗ [ x y 1 ] = [ s c a l e X ∗ x + s k e w X ∗ y + t r a n X s k e w Y ∗ x + s c a l e Y ∗ y + t r a n Y 1 ] \begin{bmatrix} &x{'}&\\ &y{'}&\\ &1&\\ \end{bmatrix}=\begin{bmatrix} &scaleX &skewX &tranX&\\ &skewY &scaleY &tranY&\\ &persp1 &persp2 &persp3&\\ \end{bmatrix}* \begin{bmatrix} &x&\\ &y&\\ &1&\\ \end{bmatrix}= \begin{bmatrix} &scaleX*x + skewX*y + tranX&\\ &skewY*x + scaleY*y + tranY&\\ &1&\\ \end{bmatrix} ⎣⎡​​x′y′1​​⎦⎤​=⎣⎡​​scaleXskewYpersp1​skewXscaleYpersp2​tranXtranYpersp3​​⎦⎤​∗⎣⎡​​xy1​​⎦⎤​=⎣⎡​​scaleX∗x+skewX∗y+tranXskewY∗x+scaleY∗y+tranY1​​⎦⎤​

Matrix实现缩放效果

x方向和y方向，分别缩放k1和k2倍 [ x ′ y ′ 1 ] = [ k 1 0 0 0 k 2 0 0 0 1 ] ∗ [ x y 1 ] = [ k 1 ∗ x k 2 ∗ y 1 ] \begin{bmatrix} &x{'}&\\ &y{'}&\\ &1&\\ \end{bmatrix}=\begin{bmatrix} &k1 &0 &0&\\ &0 &k2 &0&\\ &0 &0 &1&\\ \end{bmatrix}* \begin{bmatrix} &x&\\ &y&\\ &1&\\ \end{bmatrix}= \begin{bmatrix} &k1*x&\\ &k2*y&\\ &1&\\ \end{bmatrix} ⎣⎡​​x′y′1​​⎦⎤​=⎣⎡​​k100​0k20​001​​⎦⎤​∗⎣⎡​​xy1​​⎦⎤​=⎣⎡​​k1∗xk2∗y1​​⎦⎤​ Matrix实现平移效果

x方向和y方向，分别平移k1和k2距离

[ x ′ y ′ 1 ] = [ 0 0 k 1 0 0 k 2 0 0 1 ] ∗ [ x y 1 ] = [ x + k 1 y + k 2 1 ] \begin{bmatrix} &x{'}&\\ &y{'}&\\ &1&\\ \end{bmatrix}=\begin{bmatrix} &0 &0 &k1&\\ &0 &0 &k2&\\ &0 &0 &1&\\ \end{bmatrix}* \begin{bmatrix} &x&\\ &y&\\ &1&\\ \end{bmatrix}= \begin{bmatrix} &x+k1&\\ &y+k2&\\ &1&\\ \end{bmatrix} ⎣⎡​​x′y′1​​⎦⎤​=⎣⎡​​000​000​k1k21​​⎦⎤​∗⎣⎡​​xy1​​⎦⎤​=⎣⎡​​x+k1y+k21​​⎦⎤​

Matrix实现水平错切效果

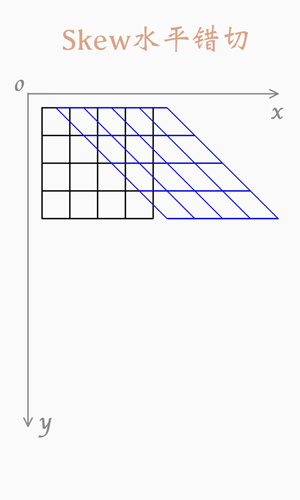水平错切，即像素的y值不变，x的值随着y的增加，平移距离越来越多，变成斜线

x像素的平移距离，是随着y值的增加，而线性增加的，系数k = Δx / Δy

[ x ′ y ′ 1 ] = [ 1 k 0 0 1 0 0 0 1 ] ∗ [ x y 1 ] = [ x + k ∗ y y 1 ] \begin{bmatrix} &x{'}&\\ &y{'}&\\ &1&\\ \end{bmatrix}=\begin{bmatrix} &1 &k &0&\\ &0 &1 &0&\\ &0 &0 &1&\\ \end{bmatrix}* \begin{bmatrix} &x&\\ &y&\\ &1&\\ \end{bmatrix}= \begin{bmatrix} &x+k*y&\\ &y&\\ &1&\\ \end{bmatrix} ⎣⎡​​x′y′1​​⎦⎤​=⎣⎡​​100​k10​001​​⎦⎤​∗⎣⎡​​xy1​​⎦⎤​=⎣⎡​​x+k∗yy1​​⎦⎤​

Matrix实现竖直错切效果

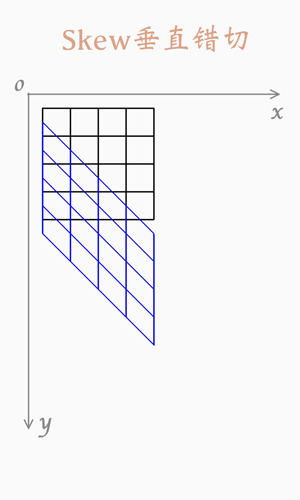竖直错切，即像素的x值不变，y的值随着x的增加，平移距离越来越多，变成斜线

y像素的平移距离，是随着x值的增加，而线性增加的，系数k = Δy / Δx

[ x ′ y ′ 1 ] = [ 1 0 0 k 1 0 0 0 1 ] ∗ [ x y 1 ] = [ x k ∗ x + y 1 ] \begin{bmatrix} &x{'}&\\ &y{'}&\\ &1&\\ \end{bmatrix}=\begin{bmatrix} &1 &0 &0&\\ &k &1 &0&\\ &0 &0 &1&\\ \end{bmatrix}* \begin{bmatrix} &x&\\ &y&\\ &1&\\ \end{bmatrix}= \begin{bmatrix} &x&\\ &k*x+y&\\ &1&\\ \end{bmatrix} ⎣⎡​​x′y′1​​⎦⎤​=⎣⎡​​1k0​010​001​​⎦⎤​∗⎣⎡​​xy1​​⎦⎤​=⎣⎡​​xk∗x+y1​​⎦⎤​ Matrix实现复合错切效果

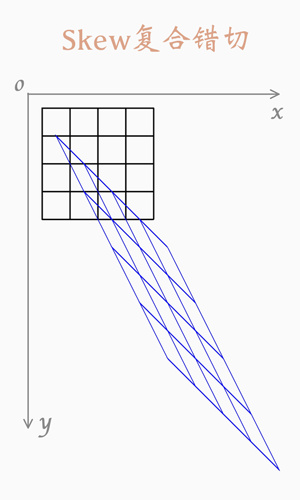通过左右、上下斜线，我们可以分别得到横切和竖切的系数k1、k2

k1 = Δx / Δy，k2 = Δy / Δx

[ x ′ y ′ 1 ] = [ 1 k 1 0 k 2 1 0 0 0 1 ] ∗ [ x y 1 ] = [ x + k 1 ∗ y k 2 ∗ x + y 1 ] \begin{bmatrix} &x{'}&\\ &y{'}&\\ &1&\\ \end{bmatrix}=\begin{bmatrix} &1 &k1 &0&\\ &k2 &1 &0&\\ &0 &0 &1&\\ \end{bmatrix}* \begin{bmatrix} &x&\\ &y&\\ &1&\\ \end{bmatrix}= \begin{bmatrix} &x+k1*y&\\ &k2*x+y&\\ &1&\\ \end{bmatrix} ⎣⎡​​x′y′1​​⎦⎤​=⎣⎡​​1k20​k110​001​​⎦⎤​∗⎣⎡​​xy1​​⎦⎤​=⎣⎡​​x+k1∗yk2∗x+y1​​⎦⎤​ Matrix实现复合旋转效果

我们先来推导旋转的矩阵公式，由图可知

x0 = r * cos α y0 = r * sin α x = r * cos(α+θ) = r * cos α * cos θ - r * sin α * sin θ = x0 * cos θ - y0 * sin θ y = r * sin(α+θ) = r * sin α * cos θ + r * cos α * sin θ = y0 * cos θ + x0 * sin θ

这个正好可以用我们的Matrix进行表示

[ x ′ y ′ 1 ] = [ c o s ( θ ) − s i n ( θ ) 0 s i n ( θ ) c o s ( θ ) 0 0 0 1 ] ∗ [ x y 1 ] = [ c o s ( θ ) ∗ x − s i n ( θ ) ∗ y s i n ( θ ) ∗ x + c o s ( θ ) ∗ y 1 ] \begin{bmatrix} &x{'}&\\ &y{'}&\\ &1&\\ \end{bmatrix}=\begin{bmatrix} &cos(θ) &-sin(θ) &0&\\ &sin(θ) &cos(θ) &0&\\ &0 &0 &1&\\ \end{bmatrix}* \begin{bmatrix} &x&\\ &y&\\ &1&\\ \end{bmatrix}= \begin{bmatrix} &cos(θ)*x-sin(θ)*y&\\ &sin(θ)*x+cos(θ)*y&\\ &1&\\ \end{bmatrix} ⎣⎡​​x′y′1​​⎦⎤​=⎣⎡​​cos(θ)sin(θ)0​−sin(θ)cos(θ)0​001​​⎦⎤​∗⎣⎡​​xy1​​⎦⎤​=⎣⎡​​cos(θ)∗x−sin(θ)∗ysin(θ)∗x+cos(θ)∗y1​​⎦⎤​

Matrix函数接口

setScale，setSkew，setTranslate，setRotate 清除矩阵之前已有的矩阵变换，将画布/画笔状态设置为新的Matrix

postScale，postSkew，postTranslate，postRotate 在旧的矩阵变换结果基础之上，再进行一次新的变换

preScale，preSkew，preTranslate，preRotate 先执行新的矩阵变换，再执行旧的矩阵变换

假设一个画布的初始状态为S0，然后分别处理了M1，M2两次变换，最终结果为S2，那么 set相当于，S2 = M2 * S0 post相当于，S2 = M2 * (M1 * S0) = (M2 * M1) * S0 pre相当于，S2 = M1 * (M2 * S0) = (M1 * M2) * S0 set和post在实际应用中，是最常用的

reset 重置到初始状态

setSinCos 通过sin，cos的值来设置旋转矩阵，setRotate的另一种方式

setValues 通过设置矩阵元素的值，来设置新的矩阵

setConcat 将连续的两次矩阵变换连接起来，作为新的矩阵，即M = M2 * M1

setRectToRect 自动计算，将一个矩形区域，转变为另一个矩形区域，所需的变换矩阵

setPolyToPoly 自动计算，将一个多边形区域，转变为另一个多边形区域，所需的变换矩阵

invert 计算当前矩阵的逆变换矩阵 比如当前矩阵向右平移了50个像素，则新的矩阵应当是-50个像素