什么是算法
算法就是解决问题的一套步骤,任何领域都存在算法,本专栏的算法则是和编程中的数据结构相关的算法
前面提到,数据结构就是数据在内存中的存储和组织方式
那么我们如何对这些数据进行添加、删除、修改、查找、排序,这就形成了一套套的算法
它们完整的说法应该是,通用数据结构操作算法
算法性能
一个算法的好坏,即性能评价指标,主要包括两方面
一是时间上的,即CPU进行了多少次运算,消耗了多长的时间
一是空间上的,即计算过程中,程序本身、用户输入、运算过程中产生的临时变量,总共占用了多大内存
时间和空间两方面的性能,有时候是不能兼得的,此时就会采用空间换时间,或者时间换空间的策略
算法复杂度
算法复杂度,是表示算法性能的一种方式,它是时间或空间关于数据量的曲线公式
类似于S(n) = k*n² + m,这里的k和m都是常量系数
我们在实际考虑算法性能时,一般主要考虑的是数据量足够大的情况
高中方程曲线学的比较好的同学的应该知道,k和m只决定曲线的平缓程度和初始位置
曲线最终的大小,主要是取决于变量n本身的增长速度的
比如n³最终会大于n²,不管k和m等于多少
所以我们在表示复杂度时,干脆将k和m等常量省去,只看最核心的部分,即S(n) = n²
这样我们就得到了这样一个最终的复杂度表示方法
- T表示时间复杂度,time的缩写
- S表示空间复杂度,storage的缩写
- O表示成本随数据量的增长变化趋势,数学中无穷大的意思
- 时间复杂度最终表示为:T(n) = O(n²)
- 空间复杂度最终表示为:S(n) = O(n²)
复杂度量级
当n趋向于无穷大时,最终决定算法成本量级的,是O参照的括号内函数
所以我们就以括号内的函数来表示复杂度量级
常见的复杂度量级有
- 常数阶O(1)
- 对数阶O(logN)
- 线性阶O(n)
- 线性对数阶O(nlogN)
- 次方阶O(nk)
- 指数阶(2n)
从上到下,复杂度量级越来越大,算法效率越来越低
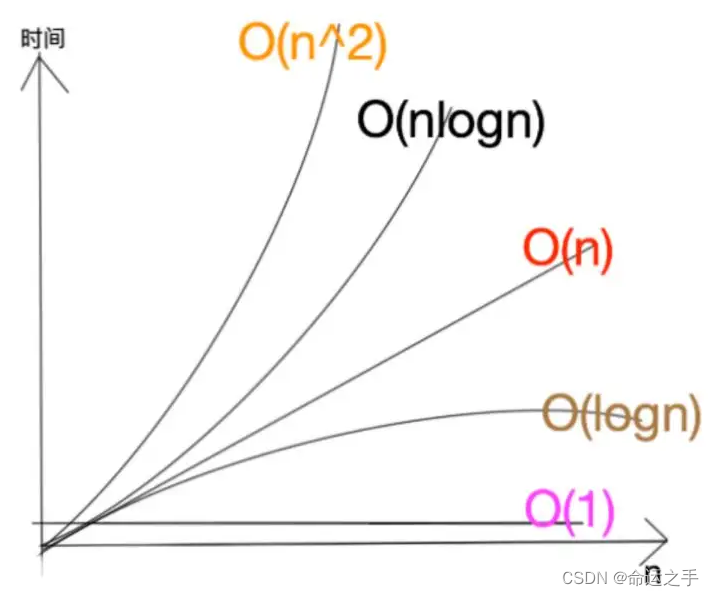
复杂度量级图像分析
我们以函数函数曲线的形式,更直观的感知不同复杂度量级,在效率上的区别