【数据结构与算法】插值查找算法、斐波那契查找算法(黄金分割法)的介绍和程序实现

1. 插值查找算法 1.1 插值查找算法的介绍

插值查找算法类似二分查找算法。二分查找算法的mid取值为 m i d = l o w + h i g h 2 = l o w + 1 2 ( h i g h − l o w ) mid =\cfrac{low + high}{2} = low + \cfrac{1}{2}(high -low) mid=2low+high=low+21(high−low)

而插值查找算法，并不是取low和high中间的index，而是根据findValue的值的大小来确定mid，findValue值偏大，则mid偏大，findValue值偏小，则mid偏小，这样能缩小查找的范围。mid取值公式为 m i d = l o w + f i n d V a l u e − a r r a y [ l o w ] a r r a y [ h i g h ] − a r r a y [ l o w ] ( h i g h − l o w ) mid = low + \cfrac{findValue - array[low]}{array[high] - array[low]}(high - low) mid=low+array[high]−array[low]findValue−array[low](high−low)

插值查找注意事项：对于数据量较大，数值分布比较均匀的有序序列来说，采用插值查找速度较快。数值分布不均匀的情况下，该方法不一定比二分查找好

1.2 插值查找算法的程序实现

需求：在一个有序数组{1, 2, 3, …, 98, 99, 100}中，用插值查找算法查找一个数在该数组的index，查找不到则返回-1

程序如下：

public class InsertValueSearch {

    public static void main(String[] args) {

        // 构建一个均匀的有序数组
        int[] array = new int[100];
        for (int i = 0; i < 100; i++) {
            array[i] = i + 1;
        }

        // 进行插值查找
        int findValueIndex = insertValueSearch(array, 0, array.length - 1, 100);
        if (findValueIndex == -1) {
            System.out.println("未找到");
        } else {
            System.out.printf("找到的值的下标是: %d\n", findValueIndex);
        }
    }
    
    /* 参数含义如下：
    low: 此次查找的最小数组下标
    high: 此次查询的最大数组下标
     */
    public static int insertValueSearch(int[] array, int low, int high, int findValue) {
        // 因为findValue参与到mid的取值，所以需要先限制findValue < array[0] || findValue > array[array.length - 1]
        // 否则求出来的mid会越界

        // 当low > high表示未找到，返回-1
        if (low > high || findValue < array[0] || findValue > array[array.length - 1]) {
            return -1;
        }

        // 根据findValue的取值，求和合适的mid值
        int mid = low + (findValue - array[low]) / (array[high] - array[low]) * (high - low);
        int midValue = array[mid];
        if (findValue > midValue) {
            // 向找到的值右边，遍历查找相同值
            return insertValueSearch(array, mid + 1, high, findValue);
        } else if (findValue < midValue) {
            // 向找到的值左边，遍历查找相同值
            return insertValueSearch(array, low, mid - 1, findValue);
        } else {
            // 如果和midValue相同，则表示找到
            return mid;
        }

    }
}

运行程序，结果如下：

找到的值的下标是: 99

2. 斐波那契查找算法 2.1 斐波那契查找算法的介绍

黄金分割点是指把一条线段分割为AB两部分，使A部分与全长之比约等于0.618，而把A部分继续分割为CD两部分，使C部分与A部分之比约等于0.618，然后按照此方法循环分割 可以借助斐波那契数列来方便的进行黄金分割点的查找。斐波那契数列：{1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …, F[k] = F[k-1] + F[k - 2]}，第一个数和第二个数为1，从第三个数开始，值为前两个数的和。而相邻的两个数之比约等于0.618 而斐波那契查找算法和二分查找算法、插值插值算法类似，只是mid得确认方法不同。斐波那契查找算法的mid就是数组index的黄金分割点，而构造一个斐波那契数列，其各个值就对应要查找的数组的多个index，就可以很方便的找到mid

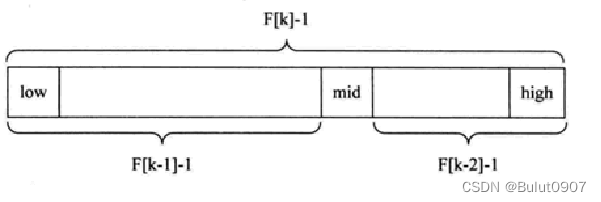求mid：因为mid位于黄金分割点，且会占用一个位置，为了便于下一次分割。所以F[k-1]-1 + 1 + F[k-2]-1 = F[k]-1，mid = low + F[k-1]-1，需要构建的数组buildArray长度 - 1为F[k]-1。确定一个合适的k，让查找的数组array的长度 - 1小于等于F[k]-1，buildArray的前面部分的值用array的值填充，后面的部分的值用array[high]填充，构建完的buildArray的index就可以方便的查找黄金分割点

2.2 斐波那契查找算法的程序实现

需求：在一个有序数组{1,8, 10, 89, 1000, 1234}中，用斐波那契查找算法查找一个数在该数组的index，查找不到则返回-1

程序如下：

import java.util.Arrays;

public class FibonacciSearch {

    public static void main(String[] args) {
        int[] array = {1, 8, 10, 89, 1000, 1234};

        // 进行斐波那契查找
        int arrayIndex = fibonacciSearch(array, 89);
        if (arrayIndex == -1) {
            System.out.println("未找到");
        } else {
            System.out.printf("找到的值的下标是: %d\n", arrayIndex);
        }
    }

    // 进行斐波那契数列的构建，即{1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ......, F[k] = F[k-1] + F[k - 2]}
    // 因为我们测试的原始数组array长度很小，这里斐波那契数组的长度为10就可以了
    public static int[] getFibonacciArray() {
        int fibonacciArraySize = 10;
        int[] fibonacciArray = new int[fibonacciArraySize];
        fibonacciArray[0] = 1;
        fibonacciArray[1] = 1;
        for (int i = 2; i < fibonacciArraySize; i++) {
            fibonacciArray[i] = fibonacciArray[i - 1] + fibonacciArray[i - 2];
        }
        return fibonacciArray;
    }

    // 斐波那契查找算法实现
    public static int fibonacciSearch(int[] array, int findValue) {
        int low = 0;
        int high = array.length - 1;
        int[] fibonacciArray = getFibonacciArray();
        // 斐波那契数组的index
        int k = 0;
        int mid;

        // 确定一个合适的k，让查找的数组array的长度 - 1小于等于F[k]-1
        // 所以构建的数组buildArray的长度为F[k]
        while (high > fibonacciArray[k] - 1) {
            k++;
        }

        // 构建的数组buildArray，buildArray的前面部分的值用array的值填充，后面的部分的值默认用0填充
        int[] buildArray = Arrays.copyOf(array, fibonacciArray[k]);

        // 再将后面的部分的值用array[high]填充
        for (int i = high + 1; i < buildArray.length; i++) {
            buildArray[i] = array[high];
        }

        // 如果low > high则表示未找到，返回-1
        while (low <= high) {
            // 求出黄金分割点mid
            mid = low + fibonacciArray[k - 1] - 1;
            // 如果比黄金分割点值小，则继续对前面一部分进行黄金分割点查找
            if (findValue < buildArray[mid]) {
                high = mid - 1;
                // 比黄金分割点值小，则这一部分是0.618那部分，即F[k-1] - 1那一部分
                // 所以k -= 1，然后再对这一部分继续进行黄金分割点查找
                k--;
                // 如果比黄金分割点值大，则继续对后一部分进行黄金分割点查找
            } else if (findValue > buildArray[mid]) {
                low = mid + 1;
                // 比黄金分割点值大，则这一部分是0.382那部分，即F[k-2] - 1那一部分
                // 所以k -= 2，然后再对这一部分继续进行黄金分割点查找
                k -= 2;
            } else {
                // 否则表示找到

                // 如果mid比high小，直接返回mid
                if (mid <= high) {
                    return mid;
                } else {
                    // 因为填充可能会导致mid比high大，如果mid比high大，则返回high
                    return high;
                }
            }
        }
        return -1;
    }
}

运行程序，结果如下：

找到的值的下标是: 3