【数据结构与算法】二叉树的介绍和程序实现

1. 二叉树的介绍

树有很多种，每个节点最多只能有两个子节点的一种形式称为二叉树。二叉树的子节点分为左节点和右节点

如果该二叉树的所有叶子节点都在最后一层，并且节点总数 = 2 n − 1 2^n -1 2n−1, n为层数，则我们称为满二叉树，如下所示：

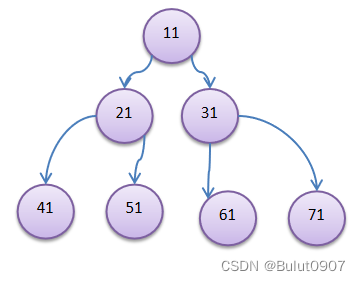
如果该二叉树的所有叶子节点都在最后一层或倒数第二层，而且最后一层的叶子节点在左边连续，倒数第二层的叶子节点在右边连续，我们称为完全二叉树。如果把 节点61删除，就不是完全二叉树了, 因为叶子节点不连续了。如下所示：

2. 二叉树的遍历说明

前序、中序、后序是根据输出父节点的顺序确定的

前序遍历

1. 先输出当前节点(初始的时候是root节点)
2. 如果左子节点不为空，则递归继续前序遍历
3. 如果右子节点不为空，则递归继续前序遍历

中序遍历

1. 如果当前节点的左子节点不为空，则递归中序遍历
2. 输出当前节点
3. 如果当前节点的右子节点不为空，则递归中序遍历

后序遍历

1. 如果当前节点的左子节点不为空，则递归后序遍历
2. 如果当前节点的右子节点不为空，则递归后序遍历
3. 输出当前节点

3. 二叉树查找指定节点说明

前序查找思路

1. 先判断当前节点的id是否等于要查找的，如果相等，则返回当前节点
2. 如果不相等。则判断当前节点的左子节点是否为空，如果不为空，则递归前序查找
3. 如果左递归前序查找，找到节点，则返回，否则继续判断当前节点的右子节点是否为空，如果不为空，则继续向右递归前序查找
4. 如果右递归前序查找，找到节点，则返回，否则返回null

中序查找思路

1. 判断当前节点的左子节点是否为空，如果不为空，则递归中序查找
2. 如果找到，则返回，如果没有找到，就和当前节点比较，如果相等则返回当前节点
3. 如果不相等，则判断当前节点的右子节点是否为空，如果不为空，则递归中序查找
4. 如果右递归中序查找，找到节点，则返回，否则返回null

后序查找思路

1. 判断当前节点的左子节点是否为空，如果不为空，则递归后序查找
2. 如果找到，就返回，如果没有找到，就判断当前节点的右子节点是否为空，如果不为空，则右递归进行后续查找，如果找到，就返回
3. 如果右递归没找到，就和当前节点进行比较，如果相等则返回
4. 如果不相等，则返回null

4. 二叉树删除指定节点说明

删除要求：如果删除的节点是叶子节点，则删除该节点；如果删除的节点是非叶子节点，则删除该子树

删除节点思路：

1. 如果root节点不为空，且删除的节点是root节点，则直接将root节点置为null
2. 如果当前节点的左子节点不为空，并且左子节点就是要删除的节点，则this.left = null，并且返回结束递归删除
3. 如果当前节点的右子节点不为空，并且右子节点就是要删除的节点，则this.right = null，并且返回结束递归删除
4. 如果第2步和第3步都没有删除节点，且当前节点的左子节点不为空，则向左子节点进行递归删除
5. 如果第4步也没有删除节点，且当前节点的右子节点不为空，则向右子节点进行递归删除

5. 二叉树的添加节点、遍历节点、查找指定节点、删除指定节点程序实现

public class BinaryTreeDemo {

    public static void main(String[] args) {
        // 创建一颗二叉树
        BinaryTree binaryTree = new BinaryTree();

        // 创建需要的节点
        Node root = new Node(1, "node1");
        Node node2 = new Node(2, "node2");
        Node node3 = new Node(3, "node3");
        Node node4 = new Node(4, "node4");
        Node node5 = new Node(5, "node5");

        // 各个节点形成子树
        root.left = node2;
        root.right = node3;
        node2.left = node4;
        node2.right = node5;

        // 将root节点添加到二叉树
        binaryTree.setRoot(root);

        // 测试遍历
        System.out.println("前序遍历：");
        binaryTree.preOrder();
        System.out.println("中序遍历：");
        binaryTree.infixOrder();
        System.out.println("后序遍历：");
        binaryTree.postOrder();

        // 测试遍历查找
        int orderSearchId = 5;
        System.out.print("前序遍历查找：");
        Node resultNode = binaryTree.preOrderSearch(orderSearchId);
        if (resultNode != null) {
            System.out.println("找到的节点信息为：" + resultNode);
        } else {
            System.out.printf("没有找到id为%d的节点\n", orderSearchId);
        }
        System.out.print("中序遍历查找：");
        resultNode = binaryTree.infixOrderSearch(orderSearchId);
        if (resultNode != null) {
            System.out.println("找到的节点信息为：" + resultNode);
        } else {
            System.out.printf("没有找到id为%d的节点\n", orderSearchId);
        }
        System.out.print("后序遍历查找：");
        resultNode = binaryTree.postOrderSearch(orderSearchId);
        if (resultNode != null) {
            System.out.println("找到的节点信息为：" + resultNode);
        } else {
            System.out.printf("没有找到id为%d的节点\n", orderSearchId);
        }

        // 测试删除节点
        System.out.printf("开始进行删除操作：");
        binaryTree.deleteNode(2);
        System.out.println("删除后进行前序遍历：");
        binaryTree.preOrder();

    }

}


// 树的Node节点
class Node {
    public int id;
    public String name;
    // 默认为null
    public Node left;
    // 默认为null
    public Node right;

    public Node(int id, String name) {
        this.id = id;
        this.name = name;
    }

    @Override
    public String toString() {
        return "Node [id = " + id + ", name = " + name + "]";
    }

    // 前序遍历实现
    public void preOrder() {
        // 先输出当前节点
        System.out.println(this);
        // 递归向左子树前序遍历
        if (this.left != null) {
            this.left.preOrder();
        }
        // 递归向右子树前序遍历
        if (this.right != null) {
            this.right.preOrder();
        }
    }

    // 中序遍历实现
    public void infixOrder() {
        // 递归向左子树中序遍历
        if (this.left != null) {
            this.left.infixOrder();
        }
        // 输出当前节点
        System.out.println(this);
        // 递归向右子树中序遍历
        if (this.right != null) {
            this.right.infixOrder();
        }
    }


    // 后序遍历实现
    public void postOrder() {
        // 递归向左子树后序遍历
        if (this.left != null) {
            this.left.postOrder();
        }
        // 递归向右子树后序遍历
        if (this.right != null) {
            this.right.postOrder();
        }
        // 输出当前节点
        System.out.println(this);
    }

    // 前序遍历查找
    public Node preOrderSearch(int id) {
        // 比较当前结点是不是
        if (this.id == id) {
            return this;
        } else {
            // 判断当前节点的左子节点是否为空，如果不为空，则递归前序查找
            Node resultNode = null;
            if (this.left != null) {
                resultNode = this.left.preOrderSearch(id);
            }
            // 如果左递归前序查找，找到节点，则返回
            if (resultNode != null) {
                return resultNode;
            } else {
                // 否则继续判断当前节点的右子节点是否为空，如果不为空，则继续向右递归前序查找
                if (this.right != null) {
                    resultNode = this.right.preOrderSearch(id);
                }
                // 如果右递归前序查找，找到节点，则返回，否则返回null
                return resultNode;
            }

        }
    }

    // 中序遍历查找
    public Node infixOrderSearch(int id) {
        // 判断当前节点的左子节点是否为空，如果不为空，则递归中序查找
        Node resultNode = null;
        if (this.left != null) {
            resultNode = this.left.infixOrderSearch(id);
        }
        // 如果找到，则返回
        if (resultNode != null) {
            return resultNode;
        } else {
            // 如果没有找到，就和当前节点比较，如果相等则返回当前节点
            if (this.id == id) {
                return this;
            } else {
                // 如果不相等，则判断当前节点的右子节点是否为空，如果不为空，则递归中序查找
                if (this.right != null) {
                    resultNode = this.right.infixOrderSearch(id);
                }
                // 如果右递归中序查找，找到节点，则返回，否则返回null
                return resultNode;
            }
        }
    }

    // 后序遍历查找
    public Node postOrderSearch(int id) {

        // 判断当前节点的左子节点是否为空，如果不为空，则递归后序查找
        Node resultNode = null;
        if (this.left != null) {
            resultNode = this.left.postOrderSearch(id);
        }
        // 如果找到，就返回
        if (resultNode != null) {
            return resultNode;
        } else {
            // 如果没有找到，就判断当前节点的右子节点是否为空，如果不为空，则右递归进行后续查找
            if (this.right != null) {
                resultNode = this.right.postOrderSearch(id);
            }
            // 如果找到，就返回
            if (resultNode != null) {
                return resultNode;
            } else {
                // 如果右递归没找到，就和当前节点进行比较，如果相等则返回
                if (this.id == id) {
                    return this;
                } else {
                    // 如果不相等，则返回null
                    return resultNode;
                }
            }
        }
    }


    // 删除节点实现。返回值表示是否删除节点
    public boolean deleteNode(int id) {
        // 如果当前节点的左子节点不为空，并且左子节点就是要删除的节点，则this.left = null，并且返回结束递归删除
        if (this.left != null && this.left.id == id) {
            this.left = null;
            return true;
            // 如果当前节点的右子节点不为空，并且右子节点就是要删除的节点，则this.right = null，并且返回结束递归删除
        } else if (this.right != null && this.right.id == id) {
            this.right = null;
            return true;
            // 否则，如果当前节点的左子节点不为空，则向左子节点进行递归删除
        } else if (this.left != null) {
            boolean isDeleteNode = this.left.deleteNode(id);
            // 如果向左递归已经删除节点，就没必要进行向右递归删除了
            if (isDeleteNode) {
                return isDeleteNode;
            } else {
                // 否则，如果当前节点的右子节点不为空，则向右子节点进行递归删除
                if (this.right != null) {
                    // 直接返回向右递归删除的结果
                    return this.right.deleteNode(id);
                }
            }
        }

        // 如果当前节点的右节点为空，则表示未找到删除的节点，返回false
        return false;
    }

}


// BinaryTree二叉树
class BinaryTree {
    private Node root;

    public void setRoot(Node root) {
        this.root = root;
    }


    // 前序遍历实现
    public void preOrder() {
        if (this.root != null) {
            this.root.preOrder();
        } else {
            System.out.println("二叉树为空，无法遍历");
        }
    }

    // 中序遍历实现
    public void infixOrder() {
        if (this.root != null) {
            this.root.infixOrder();
        } else {
            System.out.println("二叉树为空，无法遍历");
        }
    }

    // 后序遍历实现
    public void postOrder() {
        if (this.root != null) {
            this.root.postOrder();
        } else {
            System.out.println("二叉树为空，无法遍历");
        }
    }

    // 前序遍历查找
    public Node preOrderSearch(int id) {
        if (root != null) {
            return root.preOrderSearch(id);
        } else {
            return null;
        }
    }

    // 中序遍历查找
    public Node infixOrderSearch(int id) {
        if (root != null) {
            return root.infixOrderSearch(id);
        } else {
            return null;
        }
    }

    //后序遍历查找
    public Node postOrderSearch(int id) {
        if (root != null) {
            return this.root.postOrderSearch(id);
        } else {
            return null;
        }
    }

    // 删除结点实现
    public void deleteNode(int id) {
        if (root != null) {
            // 如果root节点不为空，且删除的节点是root节点，则直接将root节点置为null
            if (root.id == id) {
                root = null;
                System.out.printf("id为%d的节点已删除\n", id);
            } else {
                // 递归进行删除
                boolean isDeleteNode = root.deleteNode(id);
                if (isDeleteNode) {
                    System.out.printf("id为%d的节点已删除\n", id);
                } else {
                    System.out.println("未找到删除的节点");
                }
            }
        } else {
            System.out.println("空树，不能删除");
        }
    }
}

运行程序，结果如下：

前序遍历：
Node [id = 1, name = node1]
Node [id = 2, name = node2]
Node [id = 4, name = node4]
Node [id = 5, name = node5]
Node [id = 3, name = node3]
中序遍历：
Node [id = 4, name = node4]
Node [id = 2, name = node2]
Node [id = 5, name = node5]
Node [id = 1, name = node1]
Node [id = 3, name = node3]
后序遍历：
Node [id = 4, name = node4]
Node [id = 5, name = node5]
Node [id = 2, name = node2]
Node [id = 3, name = node3]
Node [id = 1, name = node1]
前序遍历查找：找到的节点信息为：Node [id = 5, name = node5]
中序遍历查找：找到的节点信息为：Node [id = 5, name = node5]
后序遍历查找：找到的节点信息为：Node [id = 5, name = node5]
开始进行删除操作：id为2的节点已删除
删除后进行前序遍历：
Node [id = 1, name = node1]
Node [id = 3, name = node3]