目录
1. 为什么有线索化二叉树
- 1. 为什么有线索化二叉树
- 2. 线索化二叉树的介绍
- 3. 中序线索化二叉树的程序实现
二叉树的遍历是用递归来实现的,效率相对来说会低一些。为了提高遍历的效率,就有了线索化二叉树
2. 线索化二叉树的介绍
现在我们看线索化二叉树是如何提高遍历的效率的。先将数列{1, 3, 6, 8, 10, 14}构建成一颗二叉树,如下所示:
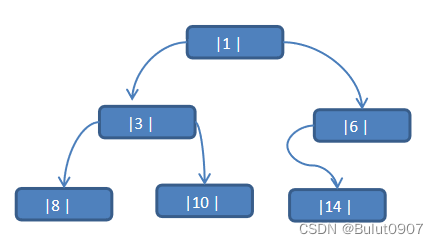
可以看到6, 8, 10, 14这几个节点的左右指针是空指针域,得出n个结点的二叉树中含有n+1【公式2n-(n-1)=n+1】个空指针域。以空间换时间的思想,将二叉树中的左空指针域,指向该节点前序/中序/后序遍历下的前一个节点(前驱节点),将二叉树中的右空指针域,指向该节点前序/中序/后序遍历下的后一个节点(后继节点)。这种附加的指针称为线索,加上线索的二叉树称为线索化二叉树(Threaded BinaryTree)
所以一个节点的左右指针域可能指向的是左右子树,也可能指向的是前驱节点/后继节点
3. 中序线索化二叉树的程序实现需求:将上面的二叉树,修改为中序线索化二叉树,然后进行遍历
中序线索化二叉树的实现思路: 上面的二叉树的中序遍历结果为:{8, 3, 10, 1, 14, 6},则修改为中序线索化二叉树的结果如下:
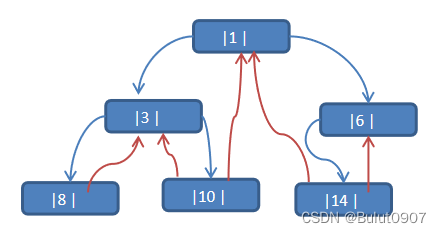 遍历中序线索化二叉树思路:
遍历中序线索化二叉树思路:
因为线索化后,各个结点指向发生变化,无需使用递归方式进行遍历,各个节点可以通过线型方式遍历。提高了遍历的效率。遍历中序线索二叉树和遍历中序二叉树的结果一样
程序如下:
public class ThreadedBinaryTreeDemo {
public static void main(String[] args) {
// 创建一颗线索化二叉树
ThreadedBinaryTree threadedBinaryTree = new ThreadedBinaryTree();
// // 创建需要的节点
Node root = new Node(1, "node1");
Node node2 = new Node(3, "node3");
Node node3 = new Node(6, "node6");
Node node4 = new Node(8, "node8");
Node node5 = new Node(10, "node10");
Node node6 = new Node(14, "node14");
// 各个节点形成子树
root.left = node2;
root.right = node3;
node2.left = node4;
node2.right = node5;
node3.left = node6;
// 将root节点添加到线索化二叉树
threadedBinaryTree.setRoot(root);
// 对中序线索化二叉树的初始二叉树进行中序线索化
threadedBinaryTree.infixThreaded();
// 以id为10的node5进行测试
Node leftNode = node5.left;
Node rightNode = node5.right;
System.out.println("id为10的node5节点的前驱结点是 = " + leftNode);
System.out.println("id为10的node5节点的后继结点是 = " + rightNode);
// 遍历线索化二叉树
System.out.println("使用线索化的方式遍历中序线索化二叉树: ");
threadedBinaryTree.infixThreadedShow();
}
}
// 树的Node节点
class Node {
public int id;
public String name;
// 默认为null
public Node left;
// 默认为null
public Node right;
// leftType等于0表示指向的是左子树, 等于1表示指向前驱节点
// rightType等于0表示指向是右子树, 等于1表示指向后继节点
public int leftType;
public int rightType;
public Node(int id, String name) {
this.id = id;
this.name = name;
}
@Override
public String toString() {
return "Node [id = " + id + ", name = " + name + "]";
}
}
// ThreadedBinaryTree线索化二叉树
class ThreadedBinaryTree {
private Node root;
// 为了实现线索化,创建一个变量指向当前结点的前驱结点
// 当前节点变化,preNode同步变化
private Node preNode = null;
public void setRoot(Node root) {
this.root = root;
}
// 重载infixThreaded方法
public void infixThreaded() {
this.infixThreaded(root);
}
// 对二叉树进行中序线索化
// 重点:其实就是进行一次二叉树的中序遍历,在这个过程中,
// 对每个节点的左空指针域赋值为前驱节点,对每个节点的右空指针域赋值为后继节点
public void infixThreaded(Node node) {
// 如果node==null, 不能线索化
if (node == null) {
return;
} else {
// 先线索化左子树
infixThreaded(node.left);
// >>>>>>开始线索化当前结点>>>>>>
// 如果当前节点的left为空指针域,则将左空指针域赋值为前驱节点
// 对于中序遍历的第一个节点,前驱节点可能为null
if (node.left == null) {
node.left = preNode;
node.leftType = 1;
}
// 重点:因为当前节点目前并不知道它的后继节点是哪个,所以只能递归到下一轮线索化时,
// 通过preNode设置node
// 如果preNode的right为空指针域,则将右空指针域赋值为后继节点
// 对于中序遍历的最后一个节点,不会递归到下一轮线索化
if (preNode != null && preNode.right == null) {
preNode.right = node;
preNode.rightType = 1;
}
// 将当前节点是下一个节点的前驱节点,便于后续的线索化
preNode = node;
// >>>>>>结束线索化当前结点>>>>>>
// 线索化右子树
infixThreaded(node.right);
}
}
// 遍历中序线索化二叉树的方法
public void infixThreadedShow() {
Node currentNode = root;
while (currentNode != null) {
// 向左循环找到leftType == 1的结点,即线索化的节点
while (currentNode.leftType == 0) {
// 因为线索化二叉树的所有节点都有left,只有第一个线索化的节点left = null,但leftType = 1
// 所以leftType == 0时, left不会为null
currentNode = currentNode.left;
}
// 然后打印线索化的节点
System.out.println(currentNode);
// 如果后面的节点是线索化的节点,则循环输出
while (currentNode.rightType == 1) {
// 因为线索化二叉树除了最后一个节点,都有right, 但最后一个节点的right为null,rightType = 0
// 所有当rightType == 1时, right不会为null
currentNode = currentNode.right;
System.out.println(currentNode);
}
// 如果后面的节点不是线索化的节点,而是右子树,则跳到右子树,循环处理
currentNode = currentNode.right;
}
}
}
运行程序,结果如下:
id为10的node5节点的前驱结点是 = Node [id = 3, name = node3] id为10的node5节点的后继结点是 = Node [id = 1, name = node1] 使用线索化的方式遍历中序线索化二叉树: Node [id = 8, name = node8] Node [id = 3, name = node3] Node [id = 10, name = node10] Node [id = 1, name = node1] Node [id = 14, name = node14] Node [id = 6, name = node6]



