【离线采样方法 Alias Method】

最近在看图算法相关的东西，先介绍一个用于其中的采样算法吧（超小声的说一句，我打算以后把看过的算法都实现一遍，提高一下工程能力）。

1. 什么叫离散分布

首先，离散分布：给你一个概率分布，是离散的，比如[1/2, 1/3, 1/12, 1/12]，代表某个变量属于事件A的概率为1/2， 属于事件B的概率为1/3，属于事件C的概率为1/12，属于事件D的概率为1/12。

2. 时间复杂度为o(N)的采样算法

首先将其概率分布按其概率对应到线段上，像下图这样：

接着产生0~1之间的一个随机数，然后看起对应到线段的的哪一段，就产生一个采样事件。比如落在0~ 1/2之间就是事件A，落在1/2~5/6之间就是事件B，落在5/6~11/12之间就是事件C，落在11/12~1之间就是事件D。  构建线段的时间复杂度为o(N)，如果顺序查找线段的话，查找时间复杂度为o(N)，如果二分查找的话，查找的时间复杂度为O(logN)。

3. 时间复杂度O(1)的采样算法——alias

alias分为两步：

1. 做表：

将概率分布的每个概率乘上N，画出柱状图。

其总面积为N，可以看出某些位置面积大于1某些位置的面积小于1，将面积大于1的事件多出的面积补充到面积小于1对应的事件中，以确保每一个小方格的面积为1，同时，保证每一方格至多存储两个事件，这样我们就能看到一个1*N的矩形啦。

表里面有两个数组，一个数组存储的是事件i占第i列矩形的面积的比例，另一个数组存储第i列中不是事件i的另一个事件的编号。

做表的时间复杂度是o(N)。

2. 根据表采样：

先生成一个0到N间的随机整数i，代表选择第i列；

再生成一个0到1间的随机数，若其小于事件i占第i列矩形的面积的比例，则表示接受事件i，否则，接收第i列中不是事件i的另一个事件。

其实你可以算下这种方式事件i的概率，完全对应原来的概率分布。

采样的时间复杂度为 o(1) 。

4. alias 可行性证明

Alias 表一定存在吗，为什么做表的的时间复杂度是o(N)？  每一轮只要有小于1的面积，就一定有大于1的面积，则一定可以用大于1的面积那部分把小于1部分给填充到1，这样就进入到了第n+1轮，而且这样每一轮都可以合成一个等于1的面积。

5. 全部代码

   

     

      

     
     

      

       import random
      
     

     

      

     
     

      

       import time
      
     

     

      

     
     

      

       import numpy 
       as np
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      

       def gen_prob(N):
      
     

     

      

     
     

      

           p = np.random.randint(
       0, 
       100, N)
      
     

     

      

     
     

      
    
       return p / np.sum(p)
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      

       def uniform(probs):
      
     

     

      

     
     

      

           sum = []
      
     

     

      

     
     

      

           tmp = 
       0
      
     

     

      

     
     

      

           category = len(probs)
      
     

     

      

     
     

      
    
       for prob 
       in probs:
      
     

     

      

     
     

      

               tmp += prob
      
     

     

      

     
     

      

               sum.append(tmp)
      
     

     

      

     
     

      

           n = np.random.uniform(
       0, 
       1)
      
     

     

      

     
     

      
    
       for i 
       in range(category):
      
     

     

      

     
     

      
        
       if n  
       1:
      
     

     

      

     
     

      

                   large.append(i)
      
     

     

      

     
     

      
    
       while small 
       and large:
      
     

     

      

     
     

      

               index_small, index_large = small.pop(), large.pop()
      
     

     

      

     
     

      

               tmp_large = probs[index_large] - (
       1 - probs[index_small])
      
     

     

      

     
     

      

               table[index_small] = index_large
      
     

     

      

     
     

      

               probs[index_large] = tmp_large
      
     

     

      

     
     

      
        
       if tmp_large > 
       1:
      
     

     

      

     
     

      

                   large.append(index_large)
      
     

     

      

     
     

      
        
       elif tmp_large < 
       1:
      
     

     

      

     
     

      

                   small.append(index_large)
      
     

     

      

     
     

      
    
       while large:
      
     

     

      

     
     

      

               index_large = large.pop()
      
     

     

      

     
     

      

               table[index_large] = 
       -1
      
     

     

      

     
     

      
    
       while small:
      
     

     

      

     
     

      

               index_small = small.pop()
      
     

     

      

     
     

      

               table[index_small] = 
       -1
      
     

     

      

     
     

      
    
       return probs, table
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      

       def alias_sample(probs, table):
      
     

     

      

     
     

      

           category = len(probs)
      
     

     

      

     
     

      

           n = np.random.randint(
       0, category)
      
     

     

      

     
     

      
    
       if table[n] == 
       -1:
      
     

     

      

     
     

      
        
       return 
       0
      
     

     

      

     
     

      

           prob = np.random.uniform(
       0, 
       1)
      
     

     

      

     
     

      
    
       if prob < probs[n]:
      
     

     

      

     
     

      
        
       return n
      
     

     

      

     
     

      
    
       return table[n]
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      

       def get_time_uniform(probs, M):
      
     

     

      

     
     

      

           nums = []
      
     

     

      

     
     

      

           start = time.clock()
      
     

     

      

     
     

      
    
       for i 
       in range(M):
      
     

     

      

     
     

      

               nums.append(uniform(probs))
      
     

     

      

     
     

      

           elapsed = (time.clock() - start)
      
     

     

      

     
     

      

           print(
       "Uniform time used:", elapsed)
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      

       def get_time_alias(probs, M):
      
     

     

      

     
     

      

           probs, table = alias_table(probs)
      
     

     

      

     
     

      

           nums = []
      
     

     

      

     
     

      

           start = time.clock()
      
     

     

      

     
     

      
    
       for i 
       in range(M):
      
     

     

      

     
     

      

               nums.append(alias_sample(probs, table))
      
     

     

      

     
     

      

           elapsed = (time.clock() - start)
      
     

     

      

     
     

      

           print(
       "Alias time used:", elapsed)
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      
 
      
     

     

      

     
     

      

       if __name__ ==  
       "__main__":
      
     

     

      

     
     

      

           N, M = 
       1000, 
       10000
      
     

     

      

     
     

      

           probs = gen_prob(N)
      
     

     

      

     
     

      

           get_time_uniform(probs, M)
      
     

     

      

     
     

      

           get_time_alias(probs, M)
      
     
   

6. 时间对比

 

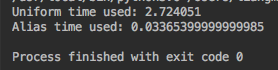
参考网址：

https://blog.csdn.net/haolexiao/article/details/65157026

https://zhuanlan.zhihu.com/p/54867139