【算法】不妨用数组实现哈夫曼树的生成

🎉每一个不曾起舞的日子，都是对生命的辜负

🎉写在前面

哈夫曼树又称最优二叉树，是一种带权路径长度最短的二叉树。所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。树的路径长度是从树根到每一结点的路径长度之和，记为WPL=（W1*L1+W2*L2+W3*L3+...+Wn*Ln），N个权值Wi（i=1,2,...n）构成一棵有N个叶结点的二叉树，相应的叶结点的路径长度为Li（i=1,2,...n）。可以证明霍夫曼树的WPL是最小的；但是今天，咱们不谈哈夫曼编码，就只用结构体配合数组来完成哈夫曼树的生成，目标是得到正确的所有权值的和。

🎉目录

构造思想

算法设计

构造实例

理解代码

 确定结构体

循环找出最小值

调用细节

 调试试图

总结

构造思想

以字符的使用频率做权构建一棵哈夫曼树，然后利用哈夫曼树对字符进行编码，俗称哈夫曼编码。具体来讲，是将所要编码的字符作为叶子结点，该字符在文件中的使用频率作为叶子结点的权值，以自底向上的方式、通过执行n-1次的“合并”运算后构造出最终所要求的树，即哈夫曼树，它的核心思想是让权值大的叶子离根最近。每次从树的集合中取出双亲为0且权值最小的两棵树作为左、右子树，构造一棵新树，新树根结点的权值为其左右孩子结点权之和，将新树插入到树的集合中。

算法设计

步骤1：确定合适的数据结构。

步骤2：初始化。构造n棵结点为n个字符的单结点树集合F={T1，T2,…, Tn}，每棵树中只有一个带权的根结点，权值为该字符的使用频率；

步骤3：如果F中只剩下一棵树，则哈夫曼树构造成功，转步骤6；否则，从集合F中取出双亲为0且权值最小的两棵树Ti和Tj，将它们合并成一棵新树Zk，新树以Ti为左儿子， Tj为右儿子（反之也可以）。新树Zk的根结点的权值为Ti与Tj的权值之和；

步骤4：从集合F中删去Ti、Tj，加入Zk；

步骤5：重复步骤3和4；

步骤6：从叶子结点到根结点逆向求出每个字符的哈夫曼编码（约定左分支表示字符“0”，右分支表示字符“1”）。则从根结点到叶子结点路径上的分支字符组成的字符串即为叶子字符的哈夫曼编码。算法结束。

构造实例

已知某系统在通信联络中只可能出现8种字符，分别为a，b，c，d，e，f，g，h，其使用频率分别为0.05，0.29，0.07，0.08，0.14，0.23，0.03，0.11，试设计哈夫曼编码。设权w=(5，29，7，8，14，23，3，11)，n=8，按哈夫曼算法的设计步骤构造一棵哈夫曼编码树，具体过程如下：

 

理解代码

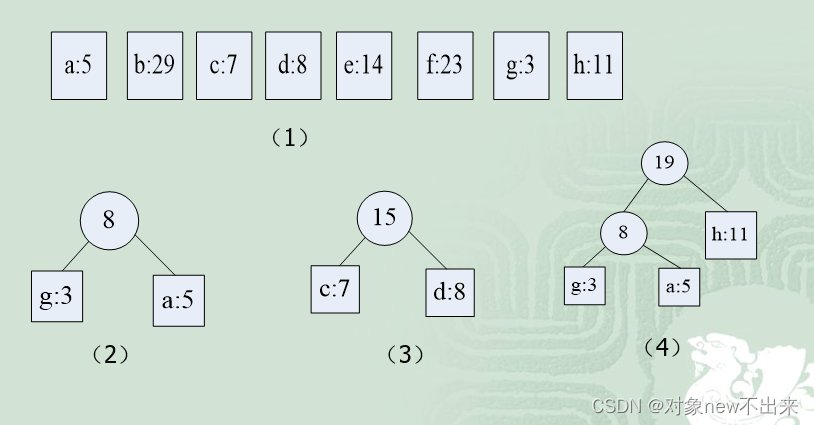
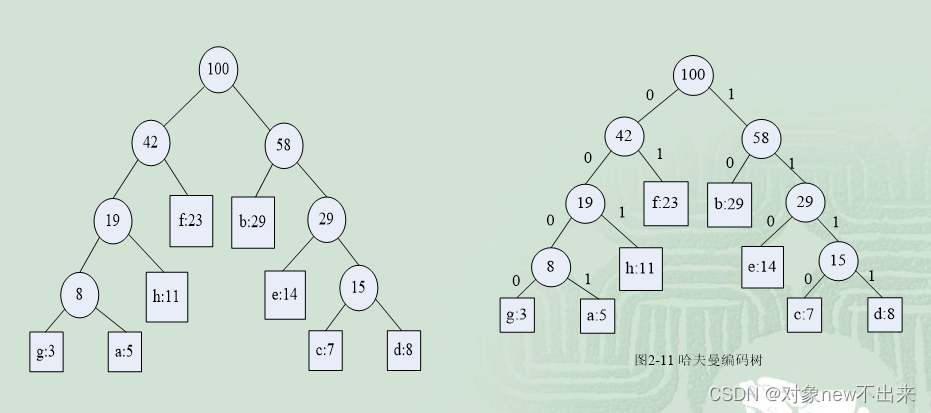
源码：

#include 
using namespace std;
#define N 8
struct Node 
{
	char L;//字母
	int K;//权值
	bool IsRoot;//是否为根结点
	int Lc, Rc;//左右子树
	Node(char l = '/0', int k = 0, bool isRoot = false) {
		L = l; K = k; IsRoot = isRoot; Lc = Rc = -1;
	}
};
Node A[N + N - 1] = { Node('a',5,true) , Node('b',29,true), Node('c',7,true), Node('d',8,true),
				      Node('e',14,true), Node('f',23,true), Node('g',3,true), Node('h',11,true) };
void FindMin(Node A[], int &min1, int &min2,int num)
{
	min1 = num - 1;
	for (int i = 0; i < num; i++) {
		if (A[i].IsRoot && A[i].K < A[min1].K) min1 = i;
	}
	min2 = num - 1;
	for (int i = 0; i < num; i++) {
		if (min1 != i && A[i].IsRoot &&A[i].K < A[min2].K) min2 = i;
	}
}
int main()
{
	int y = 1, num = N;
	int min1=0, min2=0;
	for (int i = 0; i < N; i++) {
		FindMin(A,min1,min2,num);
		A[num].K = A[min1].K + A[min2].K;
		A[num].Lc = min1;
		A[num].Rc = min2;
		A[num].IsRoot = true;
		A[min1].IsRoot = false;
		A[min2].IsRoot = false;
		A[num].L = 'h' + y;
		y++; num++;
	}
	cout