逆透视变换(IPM)多种方式及代码总结

点击上方“3D视觉工坊”，选择“星标”

干货第一时间送达

来源丨古月居

作者丨lovely_yoshino

1.背景

在自动/辅助驾驶中，车道线的检测非常重要。在前视摄像头拍摄的图像中，由于透视效应的存在，本来平行的事物，在图像中确实相交的。而IPM变换就是消除这种透视效应，所以也叫逆透视。

而我们需要认识的变换主要分为三类透视变换、仿射变换、单应性变换：

1.透视变换：不能保证物体形状的“平行性”。仿射变换是透视变换的特殊形式。透视变换是将一个平面投影到另一个平面，简单理解就是把一张图片投影到另一张图片，求的是同一张图片到它的投影图片之间的变换。

2.仿射变换：保证物体形状的“平直性”和“平行性”，一般为平移旋转等操作

3.单应性变换：由三维空间拍摄两张不同的图片来获取关键点，求的是该图片到另一个角度图片的变换，但是变换过后还是这张图片，没有变成另一个角度的图片，变换过后和另一张图片还是不同，因为三维空间得到的背景不同，所以变换过后并不能得到获取关键点对的另一张图片。

图片中的物体是一个平面图，比如用相机拍摄电脑屏幕上，（假设正面是拍正方形，侧面拍是长方形，将长方形透视变换成正方形，那么两张图片应该是一样一样的）那么单应性变换和透视变换没有什么区别。

如果我们拍的是电脑，那么不同角度得到的图片是不一样的。可能变换过后得到的电脑屏幕一样，但是从侧面拍的电脑会得到电脑侧面的信息，当变换到屏幕正面的时候就会在正面看到电脑侧面的usb插口。

2.IPM变换方法

对应点对单应变换方法

输入：至少四个对应点对，不能有三点及以上共线，不需要知道摄相机参数或者平面位置的任何信息。

数学原理：利用点对，求解透视变换矩阵，其中map_matrix是一个3×3矩阵，所以可以构建一个线性方程组进行求解。如果大于4个点，可采用ransac的方法进行求解，一边具有更好的稳定性。

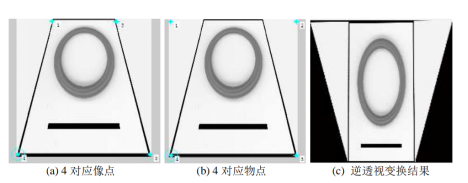
选点方法：一般采取手动选取，或者利用消影点（图像上平行线的交点，也叫消失点，vanish point）选取。

代码实现：代码实现比较简单，可以很容易实现IPM变换

计算变换矩阵：H = getPerspectiveTransform()

获取IPM图像：warpPerspective();   

- void mywarpPerspective(Mat src,Mat &dst,Mat T) {




   //此处注意计算模型的坐标系与Mat的不同


   //图像以左上点为（0,0），向左为x轴，向下为y轴，所以前期搜索到的特征点 存的格式是（图像x，图像y）---（rows，cols）


   //而Mat矩阵的是向下为x轴，向左为y轴，所以存的方向为（图像y，图像x）----（cols，rows）----（width，height）


   //这个是计算的时候容易弄混的




   //创建原图的四个顶点的3*4矩阵（此处我的顺序为左上，右上，左下，右下）


       Mat tmp(3, 4, CV_64FC1, 1);
       tmp.at < double >(0, 0) = 0;
       tmp.at < double >(1, 0) = 0;
       tmp.at < double >(0, 1) = src.cols;
       tmp.at < double >(1, 1) = 0;
       tmp.at < double >(0, 2) = 0;
       tmp.at < double >(1, 2) = src.rows;
       tmp.at < double >(0, 3) = src.cols;
       tmp.at < double >(1, 3) = src.rows;


   //获得原图四个顶点变换后的坐标，计算变换后的图像尺寸
       Mat corner = T * tmp;      //corner=(x,y)=(cols,rows)
       int width = 0, height = 0;
       double maxw = corner.at < double >(0, 0)/ corner.at < double >(2,0);
       double minw = corner.at < double >(0, 0)/ corner.at < double >(2,0);
       double maxh = corner.at < double >(1, 0)/ corner.at < double >(2,0);


       double minh = corner.at < double >(1, 0)/ corner.at < double >(2,0);
       for (int i = 1; i < 4; i++) {
           maxw = max(maxw, corner.at < double >(0, i)  /  corner.at < double >(2, i));
           minw  = min (minw,  corner.at < double >(0, i)  /  corner.at < double >(2, i));
           maxh  = max(maxh, corner.at < double >(1, i)  /  corner.at < double >(2, i));
           minh  = min (minh,   corner.at < double >(1, i)  /  corner.at < double >(2, i));


       }


   //创建向前映射矩阵 map_x, map_y




         //size(height,width)
       dst.create(int(maxh - minh), int(maxw - minw), src.type());
       Mat map_x(dst.size(), CV_32FC1);
       Mat map_y(dst.size(), CV_32FC1);


       Mat proj(3,1, CV_32FC1,1);


       Mat point(3,1, CV_32FC1,1);


      T.convertTo(T, CV_32FC1);  
   //本句是为了令T与point同类型（同类型才可以相乘，否则报错，也可以使用T.convertTo(T, point.type() );）
   Mat Tinv=T.inv();   


       for (int i = 0; i < dst.rows; i++) {        
           for (int j = 0; j < dst.cols; j++) {
               point.at(0) = j + minw ;
               point.at(1) = i + minh ;
               proj = Tinv * point;
               map_x.at(i, j) = proj.at(0)/ proj.at(2) ;
               map_y.at(i, j) = proj.at(1) / proj.at(2) ;
           }
       }
       remap(src,dst,map_x,map_y, CV_INTER_LINEAR);




   }

3.简化相机模型的逆透视变换

利用相机成像过程当中各种坐标系之间的转换关系，对其基本原理进行抽象和简化，从而得到世界坐标系和图像坐标系之间坐标的对应关系，并对逆透视变换的坐标关系进行公式化描述。这种逆透视变换形式简单，计算速度快，并且适用于复杂道路场景。

3.1 paper：Stereo inverse perspective mapping: theory and applications

这种方法需要的已知量：

这个方法同时考虑到了上下俯仰角和水平偏航角度的矫正，但是存在水平线弯曲误差，导致图像的水平横线如行道线等，恢复到世界坐标系的道路平面后，会有一定的弯曲。

3.2 Paper：Robust Inverse Perspective Mapping Based on Vanishing Point

基于消失点的俯仰角和偏航角计算

根据射影几何学原理，现实空间中的平行直线组在存在透视形变的情况下将会相交于无穷远点处，而该交点在成像平面上的投影即被称为消失点。当现实世界的平行直线组与成像平面平行时，消失点将位于成像平面的无穷远处；但是当平行直线组与成像平面部存在不平行关系时，消失点将位于成像平面的有限远处，甚至可能出现在图像区域以内。

消失点具有一些重要的性质：

• 真实道路场景中相互平行的行道线以及与其他和行道线平行的直线都指向相同的消失点；

• 某条直线对应的消失点一定位于这条直线在图像平面的投影射线方向上；

• 消失点的位置和滚转角无关，仅仅和俯仰角、偏航角有关；

• 当偏转角为90度时，行道线所对应的消失点位于道路图像水平方向外部；

• 当俯仰角为90度时，行道线所对应的消失点位于道路图像垂直方向外部；

• 当相机坐标系和世界坐标系原点完全重合时，消失点位于道路图像中心；

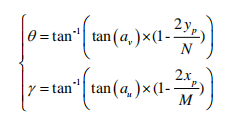
其中$( x , y )$是消失点坐标，$( M , N )$是图像宽高，($\alpha_v$,$\alpha_u$)是垂直、水平视场角的一半，由次公式可计算偏转和俯仰角

示意图如下：

由图像坐标到IPM坐标的关系式为：

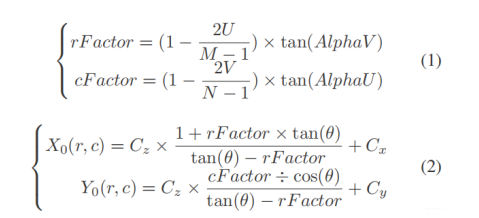
引入偏航角：

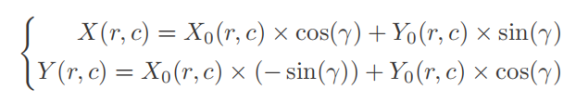
void build_ipm_table
    (
    const int srcw,
    const int srch,
    const int dstw,
    const int dsth,
    const int vptx,
    const int vpty,
    int* maptable
    )
{
    const float alpha_h = 0.5f * FOV_H * DEG2RAD;
    const float alpha_v = 0.5f * FOV_V * DEG2RAD;
    const float gamma = -(float)(vptx - (srcw >> 1)) * alpha_h / (srcw >> 1); // camera pan angle
    const float theta = -(float)(vpty - (srch >> 1)) * alpha_v / (srch >> 1); // camera tilt angle


    const int front_map_start_position = dsth >> 1;
    const int front_map_end_position = front_map_start_position + dsth;
    const int side_map_mid_position = dstw >> 1;
    //scale to get better mapped image
    const int front_map_scale_factor = 4;
    const int side_map_scale_factor = 2;


    for (int y = 0; y < dstw; ++y)
        {
        for (int x = front_map_start_position; x < front_map_end_position; ++x)
            {
            int idx = y * dsth + (x - front_map_start_position);


            int deltax = front_map_scale_factor * (front_map_end_position - x - CAMERA_POS_X);
            int deltay = side_map_scale_factor * (y - side_map_mid_position - CAMERA_POS_Y);


            if (deltay == 0)
                {
                maptable[idx] = maptable[idx - dsth];
                }
            else
                {
                int u = (int)((atan(CAMERA_POS_Z * sin(atan((float)deltay / deltax)) / deltay) - (theta - alpha_v)) / (2 * alpha_v / srch));
                int v = (int)((atan((float)deltay / deltax) - (gamma - alpha_h)) / (2 * alpha_h / srcw));
                if (u >= 0 && u < srch && v >= 0 && v < srcw)
                    {
                    maptable[idx] = srcw * u + v;
                    }
                else
                    {
                    maptable[idx] = -1;
                    }
                }
            }
        }
}

从对比结果看，此方法不会让水平线弯曲，同事使用偏航角进行修正，具有较好效果。

3.3 Paper：Adaptive Inverse Perspective Mapping for Lane Map Generation with SLAM

https://github.com/visionbike/AdaptiveIPM

这种方法利用相机位姿，在相邻帧中加入了俯仰角的修正，因此可以得到比较好的逆变换效果，下面就是相关原理示意图：

void AdaptiveIPM::ipm_based_on_vp()
{
    //根据灭点来进行反投影变换
    Point2d ptVP = m_ptVP;
    Mat imgSrc = m_SrcImg;


    int v = imgSrc.rows;
    int u = imgSrc.cols;


    ptVP.y = MAX(0, ptVP.y);


    m_ipmInfo.vpPortion = m_ipmInfo.vpInitPortion;




    FLOAT_MAT_ELEM_TYPE eps = m_ipmInfo.vpPortion * v;
    //cout<